Najmanj kvadratov

Kakšen je način minimalnih kvadratov?

Metoda Najmanj kvadratov Je ena najpomembnejših aplikacij pri pristopu funkcij. Ideja je najti krivuljo, tako da je glede na nabor urejenih parov ta funkcija bolje pristopiti k podatkom. Funkcija je lahko črta, kvadratna krivulja, kubična itd.

Ideja metode je zmanjšati vsoto kvadratov razlik v rednih (komponenta Y), med točkami, ki jih ustvari izbrana funkcija, in točkami, ki pripadajo naboru podatkov.

Najmanjša kvadratna metoda

Preden damo metodo, moramo najprej jasno, kaj "bolje se približuje". Recimo, da se išče črta y = b+mx, ki je tista, ki najbolje predstavlja niz n točk, in sicer (x1, y1), (x2, y2)…, (xn, yn).

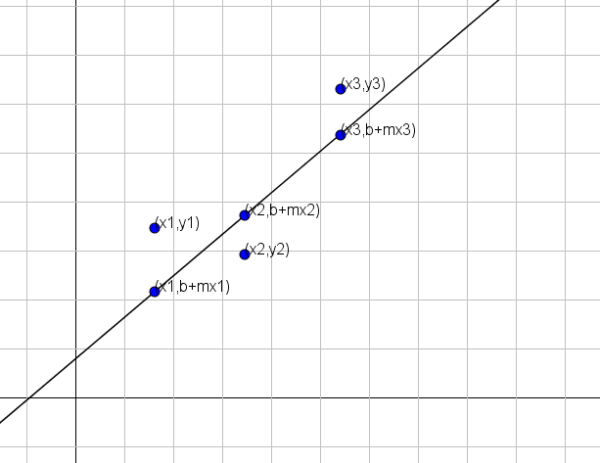
Kot je prikazano na prejšnji sliki, če sta bila spremenljivka x in y povezana s črto y = b+mx, bi bila za x = x1 ustrezna vrednost y b+mx1. Vendar se ta vrednost razlikuje od resnične vrednosti y, ki je y = y1.

Ne pozabite, da je v ravnini razdalja med dvema točkama podana z naslednjo formulo:

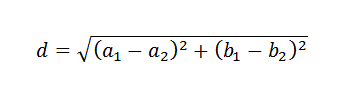
Glede na to, če želite določiti, kako izbrati črto y = b+mx, ki se najbolje približa danim podatkom in črta.

Ker je razdalja med točkami (x1, y1) in (x1, b+mx1) y1- (b+mx1), se naša težava zmanjša na iskanje številk M in B, tako da je naslednja vsota minimalna:

Vam lahko služi: zeleni teorem, demonstracije, aplikacije in vaje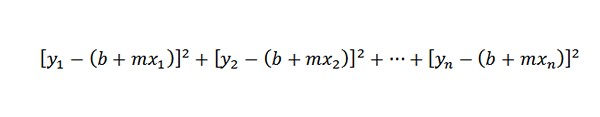

Linija, ki ustreza temu stanju, je znana kot "pristop k liniji minimalnih kvadratov do točk (x1, y1), (x2, y2), ..., (xn, yn)".

Ko je težava pridobljena, še vedno izberemo metodo za iskanje pristopa z minimalnimi kvadratki. Če so točke (x1, y1), (x2, y2), ..., (xn, yn) vse na črti y = mx+b, bi morali biti kolinealni in::

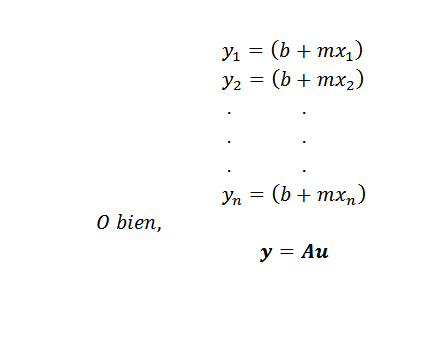
V tem izrazu:

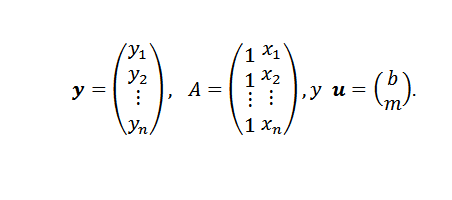
Končno, če točke niso kolinealne, potem lahko y-au = 0 in težava prevede v iskanje vektorja ali takega, da je evklidski standard minimalen.

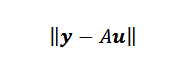
Iskanje minimizirajočega vektorja ali ni tako težko, kot bi si lahko mislili. Kot je matrika NX2, U pa je matrika 2 × 1, imamo, da je Au vektor vektor v Rⁿ in pripada podobi A, ki je podprostor Rⁿ Z dimenzijo ne več kot dve.

Domnevali bomo, da je n = 3 pokazati, kakšen je postopek, ki ga je treba upoštevati. Če je n = 3, bo slika A ravnina ali črta, ki prehaja skozi izvor.

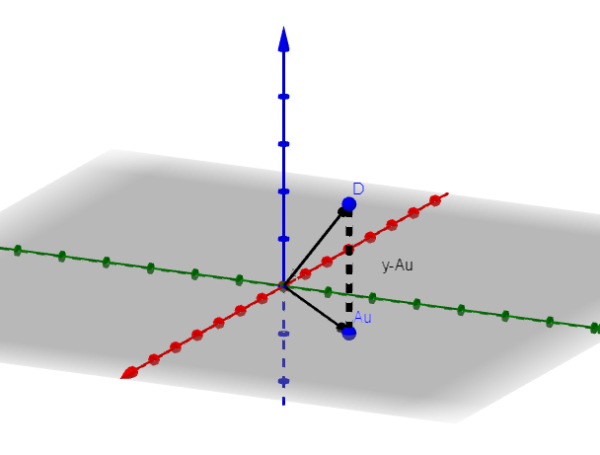
Naj v zmanjšanje vektorja. Na sliki opažamo, da je y-au čim manjši, ko je pravokotna do slike a. To pomeni, da če je V čim manjši vektor, potem se zgodi, da:

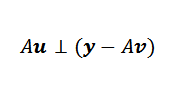
Nato lahko zgoraj na ta način izrazimo zgoraj:

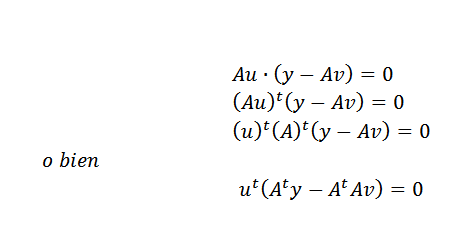
To se lahko zgodi le, če:

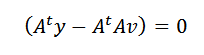
Končno, čiščenje V, moramo:

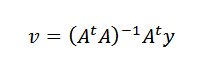
To je mogoče storiti od^tA je obrnjen, kadar koli točke kot podatki niso kolinealne.

Zdaj, če bi namesto iskanja vrstice našli prispodobo (katere izraz bi bil iz oblike y = a+bx+cx²) Da bi bil boljši približek podatkovnim točkam, bi bil postopek opisan spodaj.

Vam lahko služi: cele številke

Če bi bile podatkovne točke v tej prispodobi, bi to moralo:

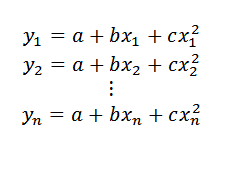
Nato:

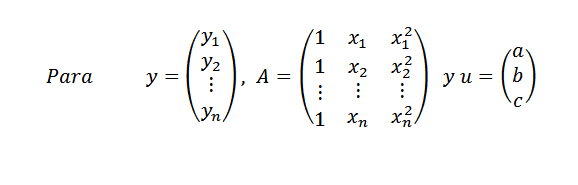
Podobno lahko napišemo y = au. Če vseh točk niso v prispodobi, imamo, da je Y-Au drugačen od ničle za kateri koli vektor u in naš problem je spet: poiščite vektor u v r3, tako da je njegova norma || y-au || biti čim več.

Ponavljanje prejšnjega postopka lahko pridemo do želenega vektorja je:

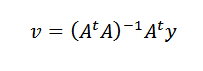
Rešene vaje

Vaja 1

Poiščite črto, ki najbolj ustreza točkam (1.4), (-2,5), (3, -1) in (4.1).

Rešitev

Moramo:

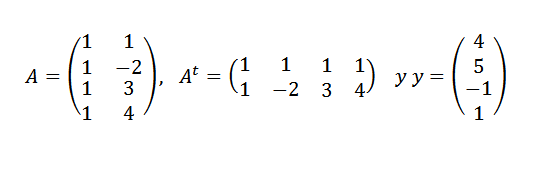
Nato:

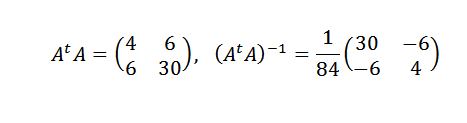
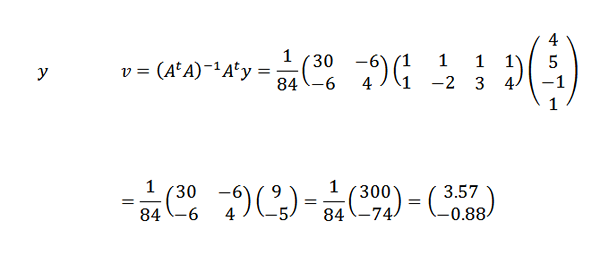
Zato sklepamo, da je črta, ki najbolj ustreza točkam, podana z:

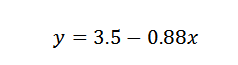
Vaja 2

Recimo, da se predmet spusti z višine 200 m. Med padcem se sprejmejo naslednji ukrepi:

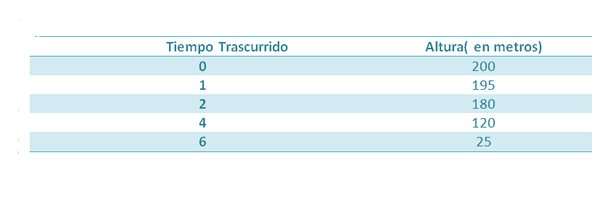
Vemo, da je višina tega predmeta, čez nekaj časa, podana:

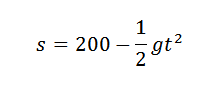
Če želimo pridobiti vrednost G, lahko poiščemo prispodobo, ki je boljši pristop do petih točk, ki so navedene v tabeli, in tako bi imeli tisti koeficient, ki ga spremlja T² To bo razumen pristop k (-1/2) g, če so meritve natančne.

Moramo:

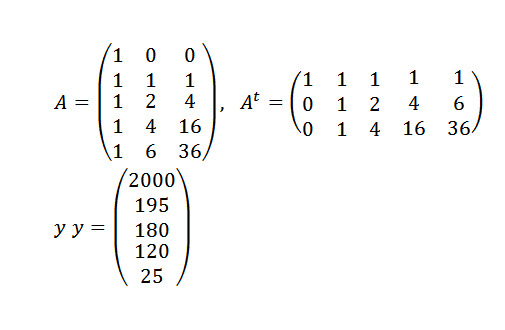
In potem:

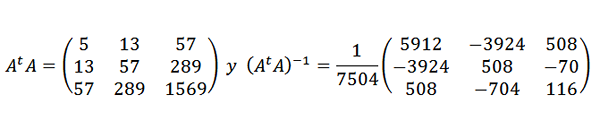
Tako se podatkovne točke prilagodijo z naslednjim kvadratnim izrazom:

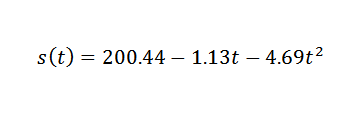
Torej moraš:

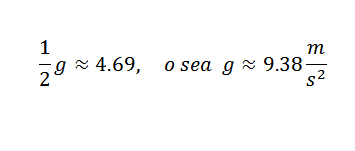
To je vrednost, ki je razumno blizu pravilnemu, ki je g = 9,81 m/s². Da bi dosegli natančnejši g g, bi bilo treba začeti iz natančnejših opazovanj.

Za kaj je minimalna kvadratna metoda za?

V težavah, ki se pojavljajo v naravnih ali družbenih vedah.

Vam lahko služi: proporcionalna variacija

Na primer, v ekonomiji lahko s preprostim formuli v ekonomiji povežemo stroške (c), dohodek (i) in dobiček (u):

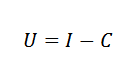
V fiziki lahko povežemo pospeševanje, ki ga povzroča gravitacija, čas, v katerem predmet pada, in višina predmeta po zakonu:

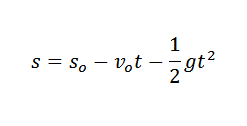
V prejšnjem izrazu s_tudi To je začetna višina omenjenega predmeta in V_tudi je vaša začetna hitrost.

Vendar iskanje takšnih formul ni preprosta naloga; Običajno ustreza dolžnosti dela, da dela s številnimi podatki in večkrat izvede več poskusov (da bi preveril, ali so pridobljeni rezultati konstantni) za iskanje odnosov med različnimi podatki.

Pogost način za to je predstaviti podatke, pridobljene v ravnini.

Eden od načinov za iskanje funkcije, ki "bolje pristopi", ki jih podajo podatki, je metoda kvadratnih minimumov.

Poleg tega, kot smo videli tudi v vaji, lahko zahvaljujoč tej metodi dosežemo precej tesne pristope k fizičnim konstantam.