Približno merjenje primerov in vadbe amorfnih številk

The Približno meritev Amorfnih številk je sestavljeno iz vrste metod, ki se uporabljajo za določitev območja ali oboda geometrijskih figur, ki niso trikotniki, kvadratki, krogi itd. Nekatere so razširjene na tri dedimenzionalne številke.

V bistvu je meritev sestavljena iz redne retikuliranja, kot so pravokotniki, kvadratki ali trapezoidi, ki pokrivajo približno površino. Natančnost pristopa območja, pridobljenega s temi metodami, se poveča s finostjo ali gostoto retikulata.

Slika 1. Kamni, oblikovani kot amorfne figure. Vir: Pxfuel.

Slika 1 in 2 prikazujeta različne amorfne številke. Za izračun območja je retikulat, sestavljen iz kvadratov 2 x 2, ki so posledično razdeljeni na dvaindvajset kvadratov 2/5 x 2/5.

Dodajanje območij glavnih kvadratov in sekundarnih kvadratov Približno območje amorfne številke dobimo.

Slika 2. Retikulat za izračun območja ene od amorfnih številk na približno način. Vir: f. Zapata

[TOC]

Območje pod krivuljo

Pogosto je treba izračunati površino pod krivuljo med dvema mejnima vrednostma. V tem primeru lahko namesto kvadratnega retikulata pravokotne črte zasledimo približno območje pod omenjeno krivuljo.

Vsota vseh pravokotnih trakov se imenuje Riemannova vsota ali vsota. Slika 3 prikazuje particijo intervala [a, b], na katerem želite približno določiti območje pod krivuljo.

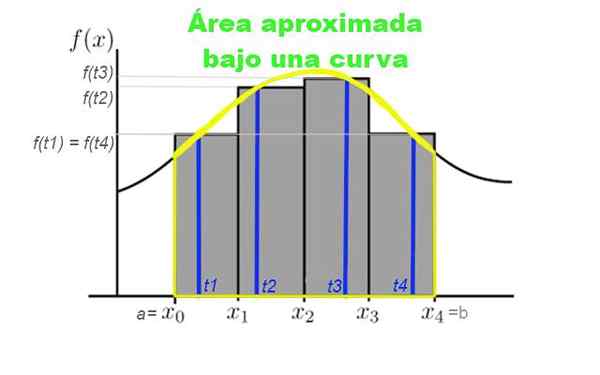Slika 3. Delitev intervala [a, b] v štirih podnožjih, ki jih običajno vzamemo iz iste širine. Višina pravokotnikov je določena z vrednostjo krivulje za TK, ki pripada podrejenim. Vir: f. Zapata.

Recimo, da želite izračunati območje pod krivuljo, ki jo daje funkcija y = f (x), kjer x pripada intervalu [a, b], v katerem želite izračunati območje. Za to je narejena delitev n elementov v tem intervalu:

Vam lahko služi: 60 delitev

Particija = x0 = a, x1, x2, ..., xn = b.

Nato je približna območje pod krivuljo, ki jo daje y = f (x) v intervalu [a, b], doseženo z naslednjim vsoto:

S = ∑_{K = 1}ⁿ f (t_k) (x_k - x_K-1)

Kjer t_k je med x_K-1 in x_k: x_K-1 ≤ t_k ≤ x_k .

Slika 3 prikazuje vsoto Riemanna krivulje y = f (x) v intervalu [x0, x4]. V tem primeru je bila narejena delitev štirih podintralov in vsota predstavlja skupno površino sivih pravokotnikov. 

Ta vsota predstavlja pristop k območju pod krivuljo F med abscisas x = x0 in x = x4.

Pristop k območju pod krivuljo se izboljšuje do te mere, da je številka n predelnih del je večje in je ponavadi točno območje pod krivuljo, ko je številka n predelne stene se nagibajo k neskončnosti. 

V primeru, da je krivulja predstavljena z analitično funkcijo, vrednosti f (t_k) Izračunani so ocenjevanje omenjene funkcije v vrednostih t_k. Če pa krivulja nima analitičnega izraza, ostajajo naslednje možnosti:

1. Pristopite k krivulji s funkcijo, na primer polinom.
2. Vzemite kartezijanske koordinate točk, kjer je krivulja prestrežena s črtami x = t_k.

Redni intervali

Odvisno od izbire vrednosti TK v intervalu [x_k, x_K-1] lahko vsota precenjuje ali podcenjuje natančno vrednost območja pod krivuljo funkcije y = f (x). Najbolj priporočljivo je, da prevzamete točko TK, kjer je manjkajoče območje približno enako preostalem območju, čeprav takšne izbire ni vedno mogoče.  

Vam lahko služi: multiplikativno inverzno: razlaga, primeri, rešene vaje

Na koncu vzemite TK

Najbolj praktična stvar je, da uporabite redne intervale širokega Δx = (b - a)/n, kjer sta A in B najmanjša in največja vrednosti abscisa, n pa število pododdelkov.

V tem primeru se območje pod krivuljo približa:

Območje = f (a+Δx)+f (a+2Δx)+…+f [a+(n-1] Δx+f (b)*Δx

V prejšnjem izrazu je bil TK odvzet na desnem koncu podintragala.

Vzemite TK na levem koncu

Druga praktična možnost je, da vzamete vrednost TK na levem koncu, v tem primeru je vsota, ki približa območje, izražena kot:

Območje = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)*Δx

TK kot osrednja vrednost

V primeru, da je TK izbran kot osrednja vrednost običajnega podintragala Δx širine, je vsota, ki približa območje pod krivuljo,:

Območje = [F (A+ΔX/2)+F (A+3ΔX/2)+…+F (B- ΔX/2)]*Δx

Vsak od teh izrazov se nagiba do natančne vrednosti, če je število pododdelkov samovoljno veliko, to pomeni, da se Δx nagiba na nič, v tem primeru pa je število izrazov vsote neizmerno veliko s posledičnimi računskimi stroški. 

Primer

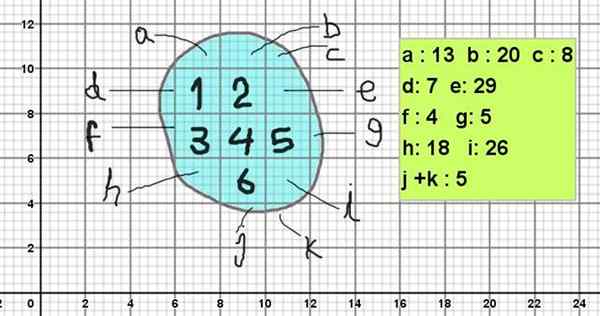
Slika 2 prikazuje amorfno figuro, katere kontura je podobna kamnom slike 1. Za izračun njenega območja je nameščen na retikulatu z glavnimi kvadratki 2 x 2 enot na kvadrat (na primer, so lahko 2 cm²).

Ker je vsak kvadrat razdeljen na 5 x 5 pododdelkov, ima vsak pododdelek površino 0,4 x 0,4 kvadratnih enot (0,16 cm²).

Slika na sliki bi bila izračunana na naslednji način:

Vam lahko služi: Skupna faktorizacija: primeri in vaje

Površina = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

To pomeni:

Površina = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Vaja rešena

Izračunajte približno območje pod krivuljo, ki jo daje funkcija f (x) = x² Stava a = -2 do b = +2. Če želite to narediti, napišite vsoto za n redne particije intervala [a, b] in nato vzemite matematično mejo za primer, da se število particij ponavadi neskončno. 

Rešitev

Prvič, interval predenja je opredeljen kot 

Δx = (b - a)/n. 

Potem je vsota za desno, ki ustreza funkciji f (x), takšen:

A = -2 in B =+2 se nadomesti tako, da je interval ali korak Δx = 4/n. V tem primeru vsota funkcije f (x) = x² je:

 Razvit je kvadratni binom: 

[-2 +(4i/n)]² = 4 - 16 i /n + (4 /n)² Yo²

In potem ga nadomestimo v znesku:

Dobimo ločevanje povzetkov in jemanje konstantnih zneskov kot skupni dejavnik vsake vsote:

 Prva vsota, drugi je:

In tretja je:

Zamenjava v izrazu vsote, ki jo imate:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

Pri izbiri velike vrednosti za n imate dober pristop do območja pod krivuljo. Vendar pa je v tem primeru mogoče doseči natančno vrednost, ki prevzame matematično mejo, ko se N nagiba k neskončnosti:

Območje = lim_{N-> ∞}[16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²]

Območje = 16 - (64/2)+ (64/3) = 16/3 = 5.333.

Reference

1. Casteleiro, J. M. 2002. Celovit izračun (ilustrirana izdaja). Madrid: uredništvo ESIC.
2. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
3. Purcell, e. 2007. Izračun z analitično geometrijo. 9na. Izdaja. Pearson Education.
4. Uničen. Zgodovina koncepta integrala. Obnovi se od: skladišče.Uničen.je
5. UIS. Riemann vsota. Okrevano od: matematika.UIS.Edu.co
6. Wikipedija. Območje. Okrevano od: je.Wikipedija.com