Izračun obratne matrice in reševanje vadbe
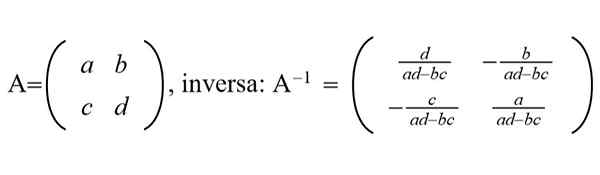
- 4961
- 1486
- Barry Ernser
The Inverzna matrica dane matrice je matrica, ki jo pomnoži izvirni rezultati v matriki identitete. Vzvratna matrica je uporabna za reševanje sistemov linearnih enačb, od tod tudi pomembnost znanja, kako jo izračunati.
Matrice so zelo koristne pri fiziki, inženiringu in matematiki, saj so kompaktno orodje za reševanje zapletenih težav. Uporabnost matric se poveča, ko so obrnjene in tudi njihova obratna je znana.
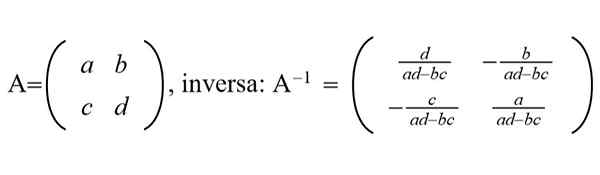 Slika 1. Prikazana je generična matrica 2 × 2 in njegova inverzna matrica. (Pripravil Ricardo Pérez)
Slika 1. Prikazana je generična matrica 2 × 2 in njegova inverzna matrica. (Pripravil Ricardo Pérez) V poljih za grafično obdelavo se veliki podatki, rudarjenje podatkov, strojno učenje in drugi uporabljajo učinkovite in hitre algoritme za oceno inverzne matrike NXN z N zelo velikimi, v vrstnem redu tisoč ali milijonov.
Za ponazoritev uporabe povratne matrice pri upravljanju sistema linearnih enačb bomo začeli z najpreprostejšim primerom vseh: 1 × 1 matrike.
Najpreprostejši primer: upošteva se linearna enačba ene same spremenljivke: 2 x = 10.
Ideja je najti vrednost x, vendar bo "matrična".
Matrica M = (2), ki pomnoži vektor (x), je matrika 1 × 1, ki ima za posledico vektor (10):
M (x) = (10)
Inverzno od matrice M označuje m-1.
Splošni način pisanja tega "linearnega sistema" je:
M x = b, kjer je x vektor (x) in b je vektor (10).
Po definiciji je povratna matrica tista, ki jo pomnoži izvirna matrika v matriki identitete I:
M-1 M = i
V primeru obravnavanega primera matrica m-1 To je matrica (½), to je m-1 = (½) od m-1 M = (½) (2) = (1) = i
Vam lahko služi: 90 delitev: kaj so in razlagaČe želite najti neznani vektor x = (x), v dvignjeni enačbi oba člana pomnožita z obratno matrico:
M-1 M (x) = m-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
Dosežena je enakost dveh vektorjev, ki sta enaka le, če so njihovi ustrezni elementi enaki, to je x = 5.
Izračun inverzne matrice
Kar motivira izračun povratne matrice, je najti univerzalno metodo za rešitev linearnih sistemov, kot je naslednji sistem 2 × 2:
x - 2 y = 3
-x + y = -2
Po korakih primera 1 × 1, preučeni v prejšnjem razdelku, sistem enačb napišemo na matrični način:
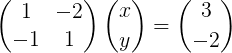 Slika 2. Linearni sistem v matrični obliki.
Slika 2. Linearni sistem v matrični obliki. Upoštevajte, da je ta sistem zapisan v kompaktni vektorski zapisi na naslednji način:
M x = b
kje
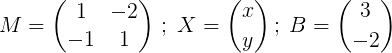
Naslednji korak je najti m.
1 metoda: z Gaussovo izločanjem
Uporabljena bo metoda izločanja Gauss. Ki je sestavljeno iz osnovnih operacij na vrstah matrice, so te operacije:
- Pomnožite vrstico s številko, ki ne.
- Dodajte ali odštejte drugo vrstico ali večkratno drugo vrstico.
- Menjalne vrstice.
Cilj je s temi operacijami pretvoriti prvotno matrico v identitetno matrico.
Kot je to storjeno, se v Matrix M uporabijo popolnoma enake operacije na matriko identitete. Ko se po več operacijah v R vrsticah spremeni v enotno matrico, se bo tisti, ki je bil prvotno enota, pretvorila v obratno matrico M, torej m-1.
Vam lahko služi: Corollary (geometrija)1- Postopek začnemo s pisanjem matrice M in zraven njega matrika enote:
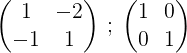
2- Dodamo dve vrsti in rezultat je postavljen v drugo vrstico, na ta način dobimo nič v prvem elementu druge vrstice:
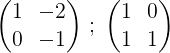
3- Drugo vrstico pomnožimo za -1, da dobimo 0 in 1 v drugi vrstici:
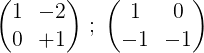
4- Prva vrstica se pomnoži z ½:

5- Drugi in prvi dodata in rezultat je postavljen v prvo vrsto:
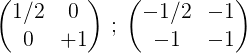
6- Za zaključek postopka se prva vrstica do 2 pomnoži, da dobimo v prvi matriki identitete, v drugi pa obratna matrika originalne matrice M:
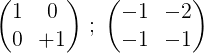
To pomeni:
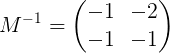
Sistemska rešitev
Ko dobite obratno matrico, se sistem enačb razreši z uporabo povratne matrice v obeh članih kompaktne vektorske enačbe:
M-1M x = m-1B
X = m-1B
To izrecno ostaja takole:
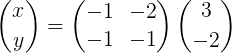
Nato je narejeno množenje matrice za pridobitev vektorja x:
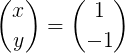
Metoda 2: s priloženo matrico
V tej drugi metodi se obratna matrika izračuna na podlagi pritrjene matrice originalne matrice Do.
Recimo matriko, ki jo daje:

kjeJaz, j Je element vrstice Yo in stolpec J matrice Do.
Pritrditev matrice Do Poklical se bo Adj (a) In njegovi elementi so:
OglasJaz, j = (-1)(i+j) ¦ai, j ..
kje Ai, j To je dopolnilna manjša matrika, ki jo dobimo z odpravo vrstice I in stolpca j iz originalne matrice Do. Palice ¦ ¦ kažejo, da se izračuna determinant, to je ¦ai, j .. Je determinant komplementarne manjše matrice.
Vam lahko služi: homologne straniFormula inverzne matrice
Formula za iskanje vzvratne matrice, ki temelji na priloženi matrici originalne matrice, je naslednja:
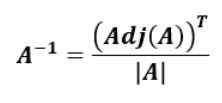
To je obratna matrica Do, Do-1, je prenos pritrditve Do deljeno z determinantom Do.
Prenosno DoTmatrice Do To je pridobljeno z izmenjavo vrst za stolpce, to je, da prva vrstica postane prva stolpec in druga vrstica do drugega stolpca in tako naprej, dokler N N vrstic prvotne matrice.
Vaja rešena
Biti matrica do naslednjega:
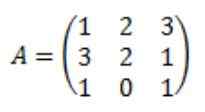
Vsak od elementov pritrjene matrice A: adj (a) se izračuna
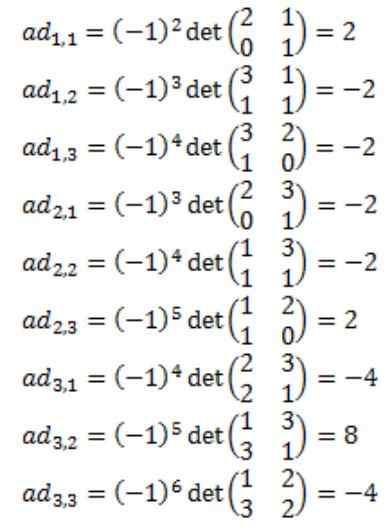
Posledica tega je, da je pritrjena matrica a, adj (a) naslednja:
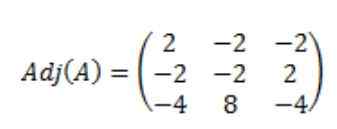
Nato se izračuna determinanta matrice A, det (a):
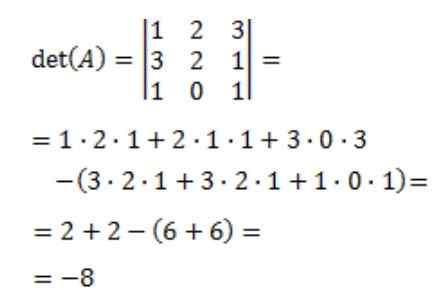
Končno dobimo obratno matrico A:
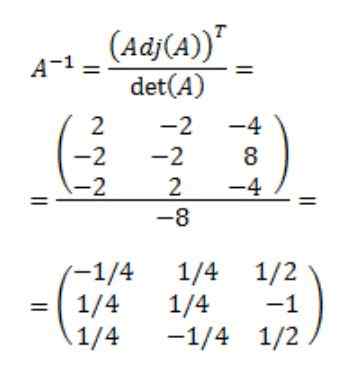
Reference
- Anthony Nicolaides (1994) Determinants & Matrices. Pass publikacija.
- AWOL ASSEN (2013) Študija o izračunu dejavnikov 3 × 3
- Casteleiro Villalba m. (2004) Uvod v linearno algebro. ESIC uvodnik.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Matematika: Vodnik za preživetje študenta. Cambridge University Press.
- Richard J. Brown (2012) 30-sekundna matematika: 50 najbolj razširjenih teorij v matematiki. Ivy Press Limited.
- Matrica. Lap Lambert Academic Publishing.
- « Polovične kulturne srednje značilnosti, vrste, uporabe
- Majevski koledarski opis, kako deluje, sistemi »

