Vektorska velikost

Kaj je vektorska velikost?

A Vektorska velikost Je vsak izraz, ki ga predstavlja vektor, ki ima numerično vrednost (modul), smer, smer in točko uporabe. Nekaj ​​primerov vektorskih velikosti je premik, hitrost, trdnost in električno polje.

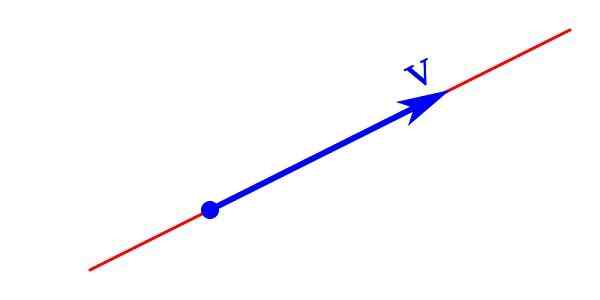
Grafični prikaz vektorske velikosti je sestavljena iz puščice, katere konica označuje njegovo smer in smer, njegova dolžina je modul in izhodišče je izvor ali točka uporabe.

Grafični prikaz vektorja

Vektorska velikost je analitično predstavljena s črko, ki nosi puščico na vrhu, ki kaže desno v vodoravni smeri. Lahko ga predstavlja tudi pismo, napisano krepko V čigar modul ǀVǀ Napisana je v poševnem tisku V.

Ena od aplikacij koncepta vektorske velikosti je v zasnovi avtocest in cest, zlasti v zasnovi njegovih zakriv. Druga aplikacija je izračun premika med dvema mestoma ali sprememba hitrosti vozila.

Elementi vektorske velikosti

Vektorska velikost je vsaka entiteta, ki jo predstavlja linijski segment, z orientacijo v vesolju, ki ima značilnosti vektorja. Njeni elementi so:

Modul: Številčna vrednost kaže na velikost ali intenzivnost vektorske velikosti.

Nagovor: To je orientacija segmenta črte v prostoru. Vektor ima lahko vodoravno, navpično ali nagnjeno smer; Sever, jug, ta ali zahod; Severovzhodno, jugovzhodno, jugozahod ali severozahod.

Smisel: Navedena je s konico puščice na koncu vektorja.

Lahko vam služi: fizika pred Grki (Antigua Grčija)

Točka prijave: To je izvor ali točka začetnega delovanja vektorja.

Vektorska klasifikacija

Vektorji so razvrščeni kot kolinearni, vzporedni, pravokotni, sočasni, sklopki, prosti, drsni, nasprotni, opremi, fiksirani in enoti.

Colineal: Pripadajo ali delujejo na isti ravni črti, imenovani so tudi linearno odvisen In so lahko navpični, vodoravni in nagnjeni.

Vzporednice: Imajo enak naslov ali naklon.

Pravokotno: Dva vektorja sta med seboj pravokotna, ko je kot med njima 90 °.

Sočasno: To so vektorji, da ob drsenju nad njihovo delovno linijo sovpadajo na isti točki v vesolju.

Koplanarios: Delujejo v ravnini, na primer letalo Xy.

prost: Premikajo se kamor koli v prostoru in ohranjajo svoj modul, smer in pomen.

Zdrs: Premikajo se po liniji delovanja, ki jo določa njihova smer.

Nasprotja: Imajo isti modul in smer ter nasprotno smer.

Oprema: Imajo isti modul, smer in pomen.

Popravljeno: Točka aplikacije je nespremenljiva.

Enota: Vektorji, katerih modul je enota.

Vektorske komponente

Vektorska velikost v tridimenzionalnem prostoru je predstavljena v sistemu treh osi, pravokotnih drug na drugega (X in z) imenovan ortogonalni poskus.

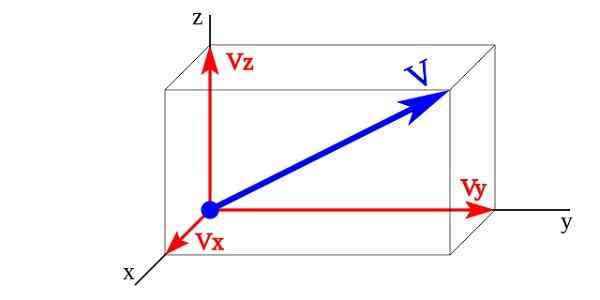Vektorske komponente vektorske magnetu

Na sliki vektorji Vx, Vy, Vz so vektorske vektorske komponente V katerih enotni vektorji so x,in,z. Vektorska velikost V Predstavljen je v vsoti njegovih vektorskih komponent.

V = Vx + Vy + Vz

Rezultat več vektorskih velikosti je vektorska vsota vseh vektorjev in te vektorje nadomešča v sistemu.

Vektorsko polje

Vektorsko polje je območje prostora, v katerem v vsaki od svojih točk ustreza vektorski velikosti. Če se manifestira velikost, je sila, ki deluje na telo ali fizični sistem, potem je vektorsko polje polje sil.

Vam lahko služi: Steinerjeva teorem: razlaga, aplikacije, vaje

Vektorsko polje je grafično predstavljeno s poljskimi črtami, ki so tangentne črte vektorske velikosti na vseh točkah v regiji. Nekaj ​​primerov vektorskih polj je električno polje, ki ga ustvari natančen električni naboj v prostoru in hitrostnim polju tekočine.

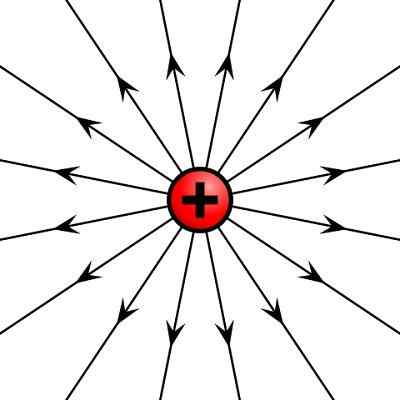Električno polje, ki ga ustvari pozitiven električni naboj

Operacije z vektorji

Dodajanje vektorjev: Je rezultat dveh ali več vektorjev. Če imate dva vektorja Tudi in Str Vsota je Tudi + P = q. Vektor Q To je dobljeni vektor, ki ga dobimo grafično premikanje izvora vektorja Do do konca vektorja B.

Odštevanje vektorja: Odštevanje dveh vektorjev ali in Str je Tudi - Str = Q. Vektor Q  Dodajate v vektor Tudi Vaše nasprotje -Str. Grafična metoda je enaka vsoti z razliko, da se nasprotni vektor prenese v skrajnost.

Skalarni izdelek: Produkt skalarne velikosti do z vektorsko velikostjo Str Je vektor MP ki ima isto smer vektorja Str. Če je skalarna velikost enaka nič, je skalarni izdelek ničelni vektor.

Primeri vektorskih velikosti

Položaj

Položaj predmeta ali delca glede na referenčni sistem je vektor, ki ga dajejo njegove pravokotne koordinate X in z, in je predstavljena z vektorskimi komponentami Xî, Yĵ, Zk. Vektorji  Yo, ĵ, k So enotni vektorji.

Delček v eni točki (X in z) ima vektor položaja r = Xî + Yĵ + Zk. Numerična vrednost vektorskega položaja je r= √ (x² + in² + z²). Sprememba položaja delcev iz enega položaja v drugega glede na referenčni sistem je vektor Premik Δr In izračuna se z naslednjim vektorskim izrazom:

Vam lahko služi: anodni žarki

Δr = r₂ - r₁

Pospešek

Povprečni pospešek (do_m) Opredeljen je kot variacija hitrosti v V časovnem intervalu ΔT In izraz za izračun je do_m= ΔV/ΔT, biti ΔV Hitrost spreminja vektorja.

Takojšen pospešek (do) je meja povprečnega pospeška do_m kdaj ΔT postane tako majhen, da se nagiba na nič. Takojšnji pospešek je izražen v skladu z vektorskimi komponentami

do =do_xYo +do_in ĵ+ do_zk

Gravitacijsko polje

Gravitacijska sila privlačnosti, ki jo izvaja masa M, Nahaja se pri izvoru, na drugi masi m V nekem trenutku v vesolju x, in, z To je vektorsko polje, imenovano Gravitacijsko polje. To silo daje izraz:

F= (-mmmg/r)ȓ

r = Xî + Yĵ + Zk

F = To je fizična gravitacijska sila

G = je univerzalna gravitacijska konstanta

ȓ = je vektor masnega položaja m

Reference

1. Tallack, j c. Uvod v vektorsko analizo. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S in Spellman, D. Analiza vektor. s.l. : MC Graw Hill, 2009.
3. Blagovna znamka, l. Analiza vektor. New York: Dover Publications, 2006.
4. Griffiths, D J. Uvod v elektrodinamiko. New Jersey: Prentice Hall, 1999. str. 1-10.
5. Haag, b. Uvod v vektorsko analizo. Glasgow: Methuen & Co. Ltd, 2012.