Vektorska algebra

Kaj je vektorska algebra?

On Vektorska algebra Gre za vejo matematike, ki je zadolžena za preučevanje sistemov linearnih enačb, vektorjev, matric, vektorskih prostorov in njihovih linearnih transformacij. Med drugim je povezan z območji, kot so inženiring, ločljivost diferencialnih enačb, funkcionalna analiza, raziskave operacij, računska grafika.

Druga od področij, ki jih je sprejela linearna algebra, je fizika, saj je bilo s tem mogoče razviti preučevanje fizičnih pojavov in jih opisati z uporabo vektorjev. To je omogočilo boljše razumevanje vesolja.

Osnove

Vektorska algebra izvira iz študije Quaterns (razširitev resničnih števil) 1, I, J in K, pa tudi kartezijske geometrije, ki sta jo spodbujala Gibbs in Heavside, ki sta se zavedala, da bodo vektorji služili kot instrument za predstavljanje zastopanja več fizičnih pojavov.

Vektorska algebra preučujemo skozi tri temelje:

Geometrijsko

Vektorji so predstavljeni z linijami, ki imajo orientacijo, operacije, kot so vsota, odštevanje in množenje z realnimi številkami, pa so opredeljene z geometrijskimi metodami.

Analitično

Opis vektorjev in njihovih operacij se izvaja s številkami, imenovanimi komponentami. Ta vrsta opisa je rezultat geometrijske predstavitve, ker se uporablja koordinatni sistem.

Aksiomatično

Opisan je opis vektorjev, ne glede na koordinatni sistem ali kakršno koli vrsto geometrijske predstavitve.

Študija številk v prostoru poteka s svojo reprezentacijo v referenčnem sistemu, ki je lahko v eni ali več dimenzijah. Med glavnimi sistemi so:

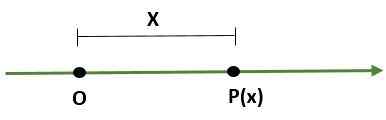
• Enodimenzionalni sistem, Da gre za črto, kjer točka (ali) predstavlja izvor in druga točka (p) določa lestvico (dolžina) in smer tega:

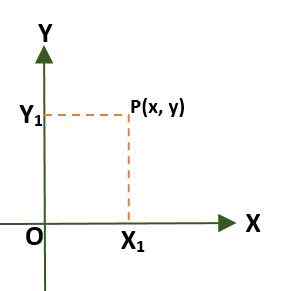
• Pravokotni koordinatni sistem (Dva -dimenzionalna), ki je sestavljena iz dveh pravokotnih linij, imenovanih osi x in y, ki prehajata skozi točkovni (ali) izvor; Na ta način je načrt razdeljen na štiri regije, imenovane kvadrante. V tem primeru je točka (p) v ravnini podana z razdaljami, ki obstajajo med osi in P.

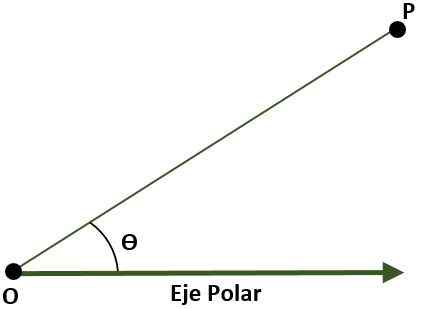
• Polarni koordinatni sistem (Dva -dimenzionalna). V tem primeru je sistem sestavljen iz točke O (izvora), ki se imenuje pol, in polčas. V tem primeru je točka p ravnine, ki se sklicuje na drog in polarno osi, podana s kotom (ɵ), ki nastane z razdaljo med izvorom in točko P.

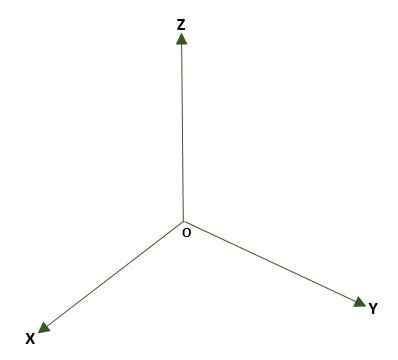
• Pravokotni tridimenzionalni sistem, tvorijo tri pravokotne črte (x, y, z), ki imajo kot svojo točko ali v vesolju. Oblikovane so tri koordinatne ravnine: xy, xz in yz; Prostor bo razdeljen na osem regij, imenovanih Octants. Referenca točke P prostora je podana z razdaljami, ki obstajajo med ravninami in P.

Velikosti

Velikost je fizična količina, ki jo je mogoče prešteti ali izmeriti s številčno vrednostjo, kot v primeru nekaterih fizičnih pojavov; Vendar je pogosto treba opisati te pojave z drugimi dejavniki, ki niso numerični. Zato so veličine razvrščene v dve vrsti:

Skalarna velikost

To so tisti zneski, ki so definirani in predstavljajo na številčni način; torej modul skupaj z mersko enoto. Na primer:

a) Čas: 5 sekund.

b) masa: 10 kg.

c) zvezek: 40 ml.

d) Temperatura: 40 ° C.

Vektorska velikost

To so tisti zneski, ki jih definira in predstavlja modul skupaj z enoto, pa tudi z občutkom in smernicami. Na primer:

Vam lahko služi: simbolizacija izrazov

a) Hitrost: (5ȋ - 3ĵ) m/s.

b) Pospešek: 13 m /s²; S 45 ° E.

c) sila: 280 n, 120 °.

d) Teža: -40 ĵ kg -f.

Vektorske magnitude so grafično predstavljene z vektorji.

Kaj so vektorji?

Vektorji so grafične reprezentacije vektorske velikosti; to pomeni, da so segmenti linij, v katerih je njegov končni konec vrh puščice.

Te so določene po modulu ali dolžini segmenta, njihovega občutka, ki ga označujeta konica puščice in njena smer glede na črto, kamor spada. Izvor vektorja je znan tudi kot točka uporabe.

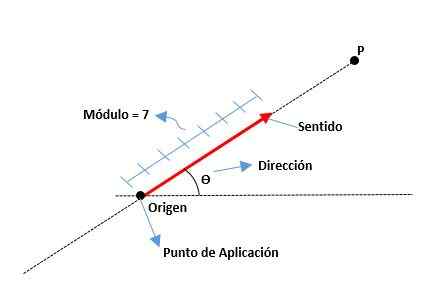
Elementi vektorja so naslednji:

Modul

To je razdalja od izvora do konca vektorja, ki jo predstavlja resnično število skupaj z enoto. Na primer:

| Om | = | A | = A = 6 cm

Nagovor

Uporabljajo se tudi mera kota, ki obstaja med osi x (od pozitivnega) in vektorjem ter kardinalnimi točkami (sever, jug, vzhod in zahod).

Smisel

Daje ga konica puščice, ki se nahaja na koncu vektorja, kar kaže, kam je to usmerjeno.

Klasifikacija vektorjev

Na splošno so vektorji razvrščeni kot:

Fiksni vektor

Je tisti, katerega aplikacijska točka (izvor) je fiksna; to pomeni, da ostaja povezan s prostorom prostora, zato se v tem ne more premakniti.

Brezplačni vektor

V vesolju se lahko prosto premika, ker se njen izvor premakne v katero koli točko, ne da bi spremenil svoj modul, pomen ali smer.

Drsni vektor

To je tisti, ki lahko svoj izvor prenese po svoji akciji, ne da bi spremenil svoj modul, pomen ali smer.

Vektorske lastnosti

Med glavnimi lastnostmi vektorjev so naslednje:

Equinecent Vectors

To so tisti prosti vektorji, ki imajo isti modul, smer (ali ti so vzporedni) in smisel kot drsni vektor ali fiksni vektor.

Enakovredni vektorji

Pojavi se, kadar imata dva vektorja enak naslov (ali sta vzporedna), enak smisel, in kljub različnim modulom in aplikacijskim točkam povzročata enake učinke.

Vektorska enakost

Ti imajo enak modul, smer in smisel, tudi če so njihova izhodišča drugačna, kar omogoča vzporedni vektor.

Nasproti vektorjev

Oni so tisti, ki imajo enak modul in smer, vendar je njihov pomen nasproten.

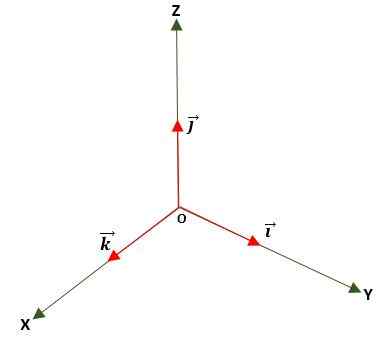
Enotni vektor

To je tisto, v katerem je modul enak enoti (1). To dobimo tako, da vektor delimo po modulu in se uporablja za določitev smeri in smeri vektorja, bodisi v ravnini ali v prostoru, z uporabo standardiziranih baznih ali enotnih vektorjev, ki so:

Ničelni vektor

Je tisti, katerega modul je enak 0; to pomeni, da se njegova točka izvora in skrajne točke sovpadata.

Vektorske komponente

Komponente vektorja so tiste vrednosti vektorskih projekcij na osi referenčnega sistema; Odvisno od razpada vektorja, ki je lahko v osi dveh ali treh dimenzij, bosta dobili dve ali tri komponente.

Komponente vektorja so realne številke, ki so lahko pozitivne, negativne ali celo nič (0).

Na ta način, če imate vektor ā, ki izvira iz pravokotnega koordinatnega sistema v XY (dvodimenzionalni) ravnini, je projekcija na osi x āx in projekcija na osi y in je āy. Tako bo vektor izražen kot vsota njegovih komponentnih vektorjev.

Primeri

Prvi primer

Imate ā vektor, ki se začne od izvora in koordinate njegovih koncev so. Tako vektor ā = (ā_x; Do_in) = (4; 5) cm.

Vam lahko služi: 120 delitev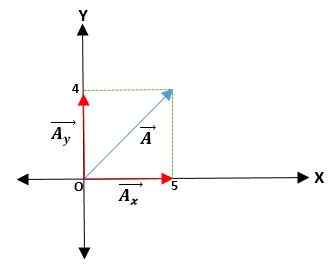

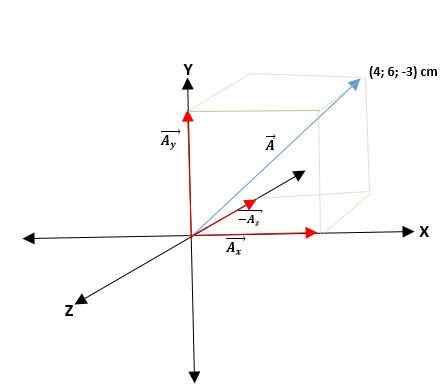
Če vektor ā deluje ob izvoru tridimenzionalnega trikotnega koordinatnega sistema (v vesolju) x, y, z, do druge točke (p), bodo projekcije na njihovih osi āx, āy in āz; Tako bo vektor izražen kot vsota njegovih treh komponentnih vektorjev.

Drugi primer

Imate ā vektor, ki se začne od izvora in koordinate njegovih koncev so. Tako vektor ā = (a_x; Do_in; Do_z) = (4; 6; -3) cm.

Vektorji, ki imajo svoje pravokotne koordinate, se lahko izrazijo v skladu z njihovimi osnovnimi vektorji. Za to je treba le vsaka koordinata pomnožiti z ustreznim enotnim vektorjem, tako da bodo za letalo in prostor naslednje:

Za letalo: ā = a_xi +a_inJ.

Za prostor: ā = a_xi +a_inJ+a_zk.

Operacije z vektorji

Obstaja veliko velikosti, ki imajo modul, pomen in smer, kot so pospeševanje, hitrost, premik, sila, med drugim.

Te se uporabljajo na različnih področjih znanosti, za njihovo uporabo.

Dodajanje in odštevanje vektorjev

Vsota in odštevanje vektorjev veljata za eno samo algebrsko operacijo, ker lahko odštevanje zapišemo kot vsoto; Na primer, odštevanje vektorjev ā in ē je mogoče izraziti kot:

Ā - ē = ā + (-ē)

Obstajajo različne metode za izvajanje vsote in odštevanja vektorjev: lahko so grafika ali analitika.

Grafične metode

Uporablja se, kadar ima vektor modul, smisel in smer. Za to so narisane črte, ki tvorijo figuro, ki pozneje pomaga določiti rezultat. Med najbolj znanimi so naslednje:

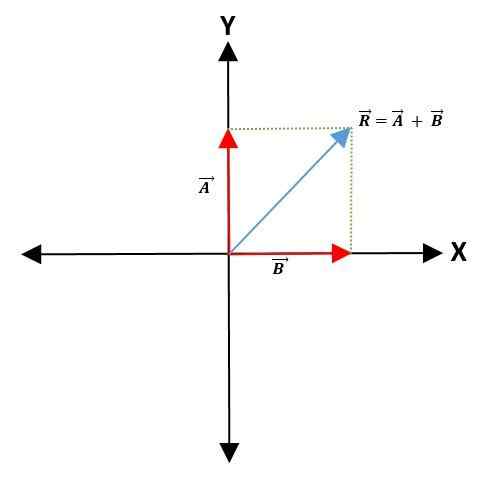
Metoda paralelograma

Za vsoto ali odštevanje dveh vektorjev je na koordinatni osi izbrana skupna točka -ki bo predstavljala točko izvora vektorjev -in ohranila njihov modul, smer in smer.

Potem se vzporedne črte vlečejo v vektorje, da tvorijo paralelogram. Nastali vektor je diagonala, ki pušča od točke izvora obeh vektorjev do točke paralelograma:

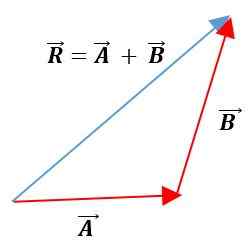
Metoda trikotnika

V tej metodi so vektorji nameščeni pod drugo, ohranjajo svoje module, čute in naslove. Nastali vektor bo zveza izvora prvega vektorja s koncem drugega vektorja:

Analitične metode

Dva ali več vektorjev lahko dodamo ali odštejemo z geometrijsko ali vektorsko metodo:

Geometrijska metoda

Ko dva vektorja tvorita trikotnik ali paralelogram, lahko M [odulo in smer dobljenega vektorja določimo z zakoni dojke in kosinusa. Tako je dobljeni vektorski modul, ki uporablja zakon kosinusa in po trikotniku, podan z:

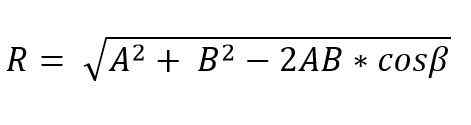
V tej formuli je β nasprotni kot do strani R, kar je enako 180 ° - ɵ.

Po drugi strani pa je po paralelogramski metodi dobljeni vektorski modul:

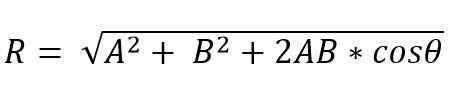
Nastali vektorski naslov je podan s kotom (α), ki tvori nastalo enega od enega od vektorjev.

Z zakonom o dojki lahko vsota ali odštevanje vektorjev opravi tudi trikotnik ali paralelogramsko metodo, saj vemo, da so v vsakem trikotniku sorazmerne dojke čednih kotov:

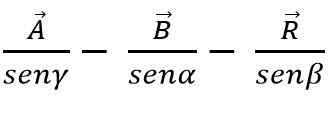
Vektorska metoda

To je mogoče storiti na dva načina: odvisno od pravokotnih koordinat ali osnovnih vektorjev.

Vektorji, ki jih bodo dodali ali odšteli do izvora koordinat, je mogoče storiti, nato pa se vse projekcije razčlenijo na njihove pravokotne komponente v vsaki osi za ravnino (x, y) ali prostora (x, x, in z); Končno se njene komponente dodajo algebraično. Torej, za letalo je:

Vam lahko služi: Primo številke: značilnosti, primeri, vaje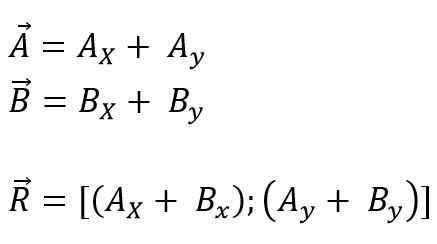

Nastali vektorski modul je:

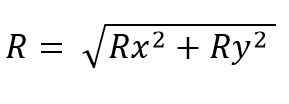
Medtem ko je za vesolje:

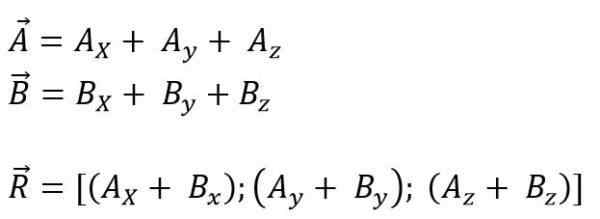
Nastali vektorski modul je:

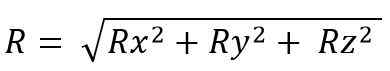
Ko se izvajajo vektorske vsote, se nanese več lastnosti, ki so:

• Asociativna lastnina: Rezultat se ne spremeni tako, da najprej dodate dva vektorja in nato dodate tretji vektor.
• Komutativna lastnina: Vrstni red vektorjev ne spremeni rezultata.
• Vektorska distribucijska lastnost: Če se skalar pomnoži z vsoto dveh vektorjev, je enak množenju skalar za vsak vektor.
• Distribucijska lastnost skalarna: Če se vektor pomnoži z vsoto dveh skalarjev, je enak množenju vektorja za vsakega skalarnega.

Vektorsko množenje

Pomnoževanje ali produkt vektorjev bi lahko izvedli kot vsota ali odštevanje, vendar pri tem izgubi fizični pomen in skoraj nikoli ni v aplikacijah. Zato so na splošno najbolj uporabljene vrste izdelkov skalarni in vektorski izdelek.

Skalarni izdelek

Znana je tudi kot točka dveh vektorjev. Ko dva vektorska modula pomnožimo z manjšim kotnim kosinusom, ki nastane med njima, dobimo skalarno. Če želite izraziti skalarni izdelek med dvema vektorji, je postavljena točka med njima in to je mogoče opredeliti kot:

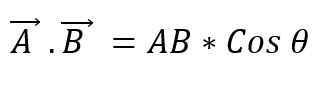
Vrednost kota, ki obstaja med obema vektorji, bo odvisna od tega, ali sta ta vzporedna ali pravokotna; Tako morate:

• Če so vektorji vzporedni in imajo enak smisel, Coseno 0º = 1.
• Če so vektorji vzporedni in imajo nasprotna čutila, Coseno 180º = -1.
• Če so vektorji pravokotni, Coseno 90 ° = 0.

Ta kot je mogoče izračunati tudi, da vedoč, da:

Skalarni izdelek ima naslednje lastnosti:

• Komutativna lastnost: Vrstni red vektorjev ne spreminja skalarne.
• Distribucijska lastnost: Če se skalarno pomnoži z vsoto dveh vektorjev, je enaka množenju skalar za vsak vektor.

Vektorski izdelek

Vektorsko množenje ali navzkrižni produkt dveh vektorjev A in B bo povzročilo nov vektor C in se izraža z uporabo križa med vektorji:

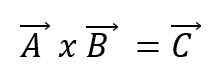
Novi vektor bo imel svoje značilnosti. Tako:

• The nagovor: Ta novi vektor bo pravokoten na ravnino, ki jo določajo prvotni vektorji.
• On smisel: To je določeno z desnim pravilom, kjer se vektor A obrne na B, ki kaže smer vrtenja s prsti, s palcem pa je smer vektorja označena.
• On modul: Določen je z množenjem modulov AXB vektorjev, s krosom manjšega kota, ki obstaja med temi vektorji. Je izraženo:

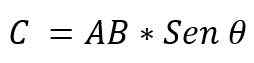
Vrednost kota, ki obstaja med obema vektorji, bo odvisna od tega, ali sta ta vzporedna ali pravokotna. Torej, mogoče je pritrditi naslednje:

• Če so vektorji vzporedni in imajo enak pomen, sine 0 ° = 0.
• Če so vektorji vzporedni in imajo nasprotna čutila, sinus 180 ° = 0.
• Če so vektorji pravokotni, sinus 90 ° = 1.

Ko je vektorski izdelek izražen v skladu z njegovimi osnovnimi vektorji, mora:

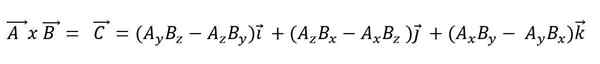
Skalarni izdelek ima naslednje lastnosti:

• Ni komutativno: vrstni red vektorjev spreminja skalarno.
• Distribucijska lastnost: Če se skalarno pomnoži z vsoto dveh vektorjev, je enaka množenju skalar za vsak vektor.