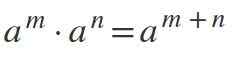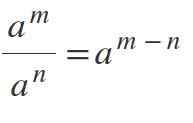Zakoni eksponentov

Kakšni so zakoni eksponentov?

The Zakoni eksponentov So tisti, ki veljajo za to številko, ki kaže, kolikokrat je treba osnovno številko pomnožiti sam. Eksponenti so znani tudi kot Powers. Potenciacija je matematična operacija, ki jo tvorijo baza (a), eksponent (m) in moč (b), kar je rezultat operacije.

Eksponenti se običajno uporabljajo, kadar se uporabljajo zelo velike količine, ker to niso nič drugega kot okrajšave, ki predstavljajo množenje tega iste številke v določeni količini. Eksponenti so lahko pozitivni in negativni.

Kaj so eksponenti v matematičnih operacijah?

Kot je navedeno zgoraj, so eksponenti skrajšana oblika, ki predstavlja množenje številk zase, kjer se eksponent nanaša le na levo številko. Na primer:

2³ = 2*2*2 = 8

V tem primeru je številka 2 osnova moči, ki se bo pomnožila 3 -krat, kot je navedeno v eksponentu, ki se nahaja v zgornjem desnem kotu podstavka. Obstajajo različni načini za branje izraza: 2 povišano na 3 ali 2 dvignjeno na kocko.

Eksponenti kažejo tudi na številokrat, ki jih je mogoče razdeliti, in za razlikovanje te operacije od množenja eksponent nosi znak minus (-) sam (je negativen), kar pomeni, da je eksponent v imenovalcu delček. Na primer:

2^{- 4} = 1/2*2*2*2 = 1/16

Tega ne bi smeli zamenjati s primerom, v katerem je osnova negativna, saj bo odvisna od tega, ali je eksponent enakomeren ali neparen, da ugotovi, ali bo moč pozitivna ali negativna. Tako moraš:

- Če je eksponent enakomeren, bo moč pozitivna. Na primer:

(-7)² = -7 _* -7 = 49.

- Če je eksponent čuden, bo moč negativna. Na primer:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Obstaja poseben primer, v katerem je, če je eksponent enak 0, moč enaka 1. Obstaja tudi možnost, da je osnova 0; V tem primeru bo moč, odvisno od eksponenta, nedoločena ali ne.

Za izvajanje matematičnih operacij z eksponenti je potrebno.

Kakšni so zakoni eksponentov?

Prvi zakon: moč eksponenta enaka 1

Ko je eksponent 1, bo rezultat enaka vrednost kot osnova: a¹ = a.

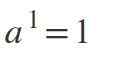
Primeri

9¹ = 9.

22¹ = 22.

895¹ = 895.

Drugi zakon: moč eksponenta, enaka 0

Ko je eksponent 0, če je osnova drugačna od ničle, bo rezultat: a⁰ = 1.

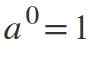
Primeri

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Tretji zakon: negativni eksponent

Ker je eksponent negativen, bo rezultat del, kjer bo moč imenovalec. Na primer, če je m pozitiven, potem^-m = 1/a^m.

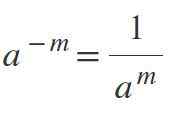
Primeri

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Četrti zakon: množenje enakih sil z istimi

Pomnožiti moči, kjer so baze enake in se razlikujejo^m _* doⁿ = a^m+n.    

Primeri

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^enajst

Peti zakon: Oddelek za oblast z isto osnovo

Za delitev moči, pri katerih so baze enake in se razlikujejo od 0, se vzdržuje podlaga in eksponenti se odštejejo na naslednji način: a^m / doⁿ = a^M-N.    

Primeri

- 9² / 9¹ = 9 ^{(enaindvajset)} = 9¹.

- 6^petnajst / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Šesti zakon: množenje različnih sil z drugačno osnovo

V tem zakonu je nasprotno od tistega, kar je izraženo v četrtem; To pomeni, da če imate različne podlage, vendar z istimi eksponenti, se baze pomnožijo in se vzdržuje eksponent: a^m _* b^m = (a_*B ^m.

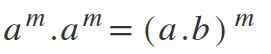
Primeri

- 10² _* dvajset² = (10 _* dvajset)² = 200².

- Štiri. Pet^enajst _* 9^enajst = (45*9)^{11 =} 405^enajst.

Drug način za zastopanje tega zakona je, ko je množenje visoko do moči. Tako bo eksponent pripadal vsakemu izrazu: (a_*B^m= a^m_* b^m.

Primeri

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Sedmi zakon: Različna delitev moči

Če imate različne podlage, vendar z enakimi eksponenti razdelite baze in se eksponent vzdržuje:^m / b^m = (a / b)^m.

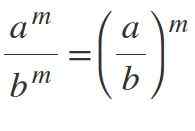
Primeri

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

Podobno, ko je delitev visoka na moči, bo eksponent pripadal vsakemu od izrazov: (a / B ^m = a^m /b^m.

Primeri

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Obstaja primer, v katerem je eksponent negativen. Torej, če je pozitiven, se vrednost števca vloži z vrednostjo imenovalca, kot sledi:

- (A / B)^-n = (b / a)ⁿ = bⁿ / doⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Osmi zakon: moč moči

Ko imate moč, ki je dvignjena na drugo moč -to je, se hkrati vzdržujeta dva eksponenta -vzdržujemo se in se eksponenti pomnožijo: (a^m)ⁿ= a^m*n.

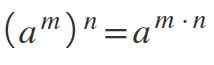
Primeri

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Deveti zakon: delni eksponent

Če ima moč kot eksponent delček, se to reši tako, da jo spremenite v korenino N-esima, kjer števca ostane kot eksponent in imenovalec predstavlja korenski indeks:

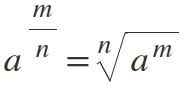
Primer

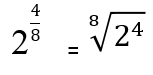
Rešene vaje

Vaja 1

Izračunajte operacije med pooblastili, ki imajo različne podlage:

2⁴ _* 4⁴ / 8².

Rešitev

Z uporabo pravil eksponentov se baze pomnožijo v števcu in eksponent se vzdržuje, kot je ta:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Zdaj, saj obstajajo enake podlage, vendar se z različnimi eksponenti vzdržuje baza in se eksponenti odštejejo:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Vaja 2

Izračunajte operacije med visokimi silami na drugo moč:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Rešitev

Če uporabite zakone, morate:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Reference

1. Aponte, g. (1998). Osnovne osnov matematike. Pearson Education.
2. Corbalán, f. (1997). Matematika, ki se uporablja za vsakdanje življenje.
3. Jiménez, J. R. (2009). Matematika 1 sep.
4. Max Peters, w. L. (1972). Algebra in trigonometrija.
5. Rees, str. K. (1986). Reverte.