Znaki zakon

Pojasnjujemo zakon znakov, s primeri in reševanimi vajami

Shema zakona o znakih

Kaj je zakon znakov?

The Znaki zakon To je nabor pravil, ki se uporabljajo v aritmetičnih in algebrskih izračunih z realnimi številkami, da pravilno dodelimo znak, ko so vpleteni tako pozitivni kot negativni zneski.

Obstajajo ustrezna pravila v skladu z izvajanjem operacije: vsota, odštevanje, množenje in delitev, ki so najosnovnejša, obstajajo pa tudi pravila znakov, povezanih s potencialnimi in vložitvami.

V dani operaciji, bodisi z roko ali s kalkulatorjem, je treba pravilno uporabiti zakon znakov, da se zagotovi pravilen rezultat, saj le majhna sprememba znakov bistveno spremeni zneske.

Zakon znakov za vsako osnovno aritmetično delovanje in primere, ki se lahko pojavijo, se preučijo spodaj.

Zakon znakov v skupni povzetki

1) Če imajo številke, ki jih je treba dodati, isti znak

Številke so dodane kot običajno in rezultat se doda v znak številk, ne glede na to, ali je to pozitivno ali negativno.

Pomembno je upoštevati, da pozitivne številke običajno niso pred znakom, ampak so napisane neposredno. Po drugi strani so negativne številke zapisane v oklepajih, zlasti kadar jih pred simbolom aritmetične operacije, da bi se izognili zmedi.

Primeri vsote števil z enakim znakom:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Če imajo številke, ki jih je treba dodati, drugačen znak

Številke se odštejejo in znak, ki ima največjo absolutno vrednost.

Kot primer izvedite operacijo 5 + (−14). Ker je absolutna vrednost (−14) večja od absolutne vrednosti 5, se od 14 odšteje 5 enot, kar daje 9 in ta rezultat je postavljen negativni znak:

Vam lahko služi: prizme in piramide

5 + (−14) = −9

Več primerov tega pravila, ki se uporablja za vsoto dveh števil različnih znakov, je:

(−27) + 12 = −15

12 + (−7) = 5

Če v operaciji obstaja več kot dva dodatka z različnimi znaki, asociativna lastnost vsote:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operacija se prvič izvaja v Pracete, ki je sestavljena iz vsote dveh števil različnih znakov, za katere se uporablja opisano pravilo: rezultat se odšteje in znak številke z najvišjo absolutno vrednostjo:

(−20) + 9 = −11

Operacija je takšna:

(−20) + 9 + (−7) = (−11) + (−7)

Zdaj imate vsoto dveh številk istega znaka, nato pa jih običajno dodamo in rezultat je postavljen negativen znak:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Znaki v nadomestku

Odštevanje dveh števil je opredeljeno kot vsota nasprotnega. Po drugi strani je nasprotno od števila navedena številka s spremenjenim znakom. Na primer, nasprotno 2 je (−2), nasprotno (−5) je 5 in tako naprej.

Glede na to, ko imate odštevanje dveh števil:

A - b

Preprosto se spremeni v vsoto nasprotja B:

A + ( - b)

In nadaljujte, kot je opisano v prejšnjem razdelku. Opomba, če želite postaviti znak + negativno število ga ne spremeni, ampak zelo previdno, nasprotno ni res.

Ko je številka "A", ki je minimalna, večja od števila "B", ki je ukradena, deluje kot pri odštevanju naravnega števila. Brez problema, saj se od manjšega zneska odšteje veliko število:

Vam lahko služi: neenakost trikotnika: demonstracija, primeri, rešene vaje

25 - 8 = 17

Z naslednjimi primeri je metoda dodajanja nasprotnega odštevanju zelo priročna:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Zakon znakov pri množenju

Zakon znakov v množenju se uporablja na ta način:

• Z množenjem dveh številk istega znaka je rezultat vedno pozitiven.
• Izdelek dveh nasprotnih številk znakov je vedno negativen.

Povzetek pravila znakov za množenje je prikazan na sliki:

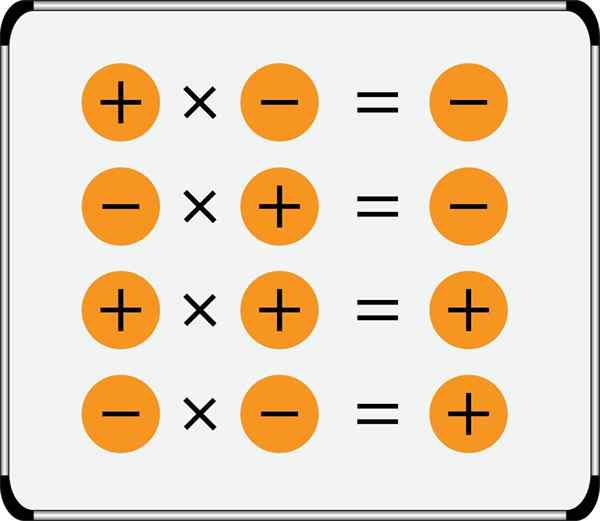
Upoštevajte, da se pozitivne številke lahko zapišejo brez prejšnjega znaka, vendar negativne številke vedno imajo, poleg tega sta dva aritmetična simbola nikoli zapisana drug drugemu, vedno morata biti ločena z oklepajem, na primer:

Napačno: 3 × −4
Pravilno: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Za pomnožitev več kot dveh številk se uporablja asociativna lastnost množenja, saj vrstni red dejavnikov ne spremeni izdelka, na primer pri izvajanju:

(−2) × (−14) × 16

Če želite, lahko pomnožite prva dva dejavnika ali zadnja dva, nato pa rezultat pomnožite s preostalim faktorjem. V tem primeru se bosta dva dejavnika najprej pomnožila na levi:

[(−2) × (−14)] × 16

Produkt dveh negativnih števil je pozitiven, nato (−2) × (−14) = 28 in ostaja:

28 × 16 = 448

Zakon znakov v delitvi

Je analogen pravilu znakov za množenje:

• Razmerje dveh številk istega znaka je vedno pozitivno.
• Z delitvijo dveh sicer številk znakov je rezultat vedno negativen.

Lahko vam služi: razlika med krogom in obodom (s primeri)

Na primer:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Zakon znakov pri opolnomočenju in vložitvi

Pisna številka exponent je:

doⁿ

Kjer je "a" osnova in "n" je eksponent. Glede na pariteto eksponenta se razlikujeta dva primera:

Primer 1: A je pozitiven

Kadar je osnova pozitivna, je rezultat pozitiven, ne glede na to, ali je eksponent enakomeren ali neparen, kot v:

2³ = 8
3⁴ = 81

Primer 2: A je negativen

Tu sta dva primera:

• Ko je eksponent enakomeren, je rezultat pozitiven.
• Če je eksponent čuden, je negativen.

Primeri

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operacije s simboli za razvrščanje

Pogosto se pojavljajo ločene operacije s simboli za združevanje: oklepaji, oklepaji in ključi. Ti se odpravljajo od znotraj navzven ob upoštevanju naslednjega:

• Če je pred skupinskim simbolom pozitiven znak, ga je mogoče odstraniti, ne da bi spremenili znake vsebine, na primer: + (−3 + 5 - 1) = −3 + 5 - 1 = 1 = 1.
• Če je negativni znak pred simbolom skupine, ga umaknemo z vlaganjem znaka vsebine, na primer: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Kadar obstajajo kombinirane operacije vsote, odštevanja, množenja in delitve, se lahko za udobje uporabijo asociativne in distribucijske lastnosti.

Rešene vaje

a) 10 + 10

Rešitev: 20

b) (-8) + (-3)

Rešitev: -11

c) (3) + (-10) 

Rešitev: -7

d) (5) x (-3)

Rešitev: -15

e) (-10) x (-10)

Rešitev: 100

f) (18) ÷ (-3)

Rešitev: -6

G) (-10) ÷ (-2)

Rešitev: 5

h) 4 - ( - 7 + 9)

Rešitev: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11 - 9 = 2