Fickov zakon

Kaj je Fickov zakon?

The Fickov zakon Gre za matematično enačbo, ki povezuje masni pretok, razširjen v mediju s koncentracijami ali gradientom pritiska. Oblikoval ga je leta 1855 nemški fiziolog in zdravnik Adolf Fick, ki ga je navdihnil Fourierovi zakoni (termična prevodnost) in OHM (električna prevodnost).

Fick's Law predstavlja posebnost, da ni uporabna samo za kemične ali biokemične difuzijske pojave, ampak tudi za tiste narave. Zato služi za modeliranje razširjanja atomov med trdnimi snovmi, saj je zelo uporabna pri fiziki materialov in inženiringa.

Predstavitev difuzijskega procesa skozi polprepustno membrano. Vir: Gabriel Bolívar.

Vendar je osrednja osnova enaka za skoraj vse difuzijske pojave, kar je prikazano zgoraj. Vijolični delci, atomi ali molekule, se širijo skozi polprepustno debelo membrano L in prečno območje do. Na levi imamo večjo koncentracijo c₁ delcev, ki na desni, c₂.

Fickov zakon določa naslednje: masni tok, ki se širi skozi površino₂-C₁/L) in konstanta d, imenovana difuzijska ali difuzivnost koeficienta.

Ta zakon ima dve obliki: ena, ki temelji na prostoru (x), in drugega, odvisno od prostora in časa (x, t). Prva velja za sisteme v stacionarnih pogojih, drugi za resnične, nestacionalne sisteme.

Fickov prvi zakon

Komponente in enačba

Debela l polprepustne membrane predstavlja razdaljo (x), ki jo morajo delci potovati, da dosežejo drugo stran. Kot je razvidno iz slike, vijolični delci, bolj se oddaljujejo od levega predela, kjer je c₁ Je super, njegova koncentracija se zmanjša na vrednost c₂. To pomeni, da se koncentracija spreminja vzdolž debeline membrane in je odvisna od x.

Ta nihanje koncentracije, odvisno od razdalje, je tisto, kar je znano kot koncentracijski gradient: (c₂-C₁)/L o (c₂-C₁)/x. Upoštevajte, da je njegova vrednost negativna (-1), ker c₂ > C₁.

Po drugi strani imamo tudi hitrost, s katero se delci širijo po membrani ali zadevnem prostoru. Ta hitrost je odvisna od velikosti in mase delcev, pa tudi od narave okolja in temperature. Difuzijski koeficient d predstavlja to hitrost in je lahko konstanten ali ne med difuzijo.

Vam lahko služi: laboratorijski filter): značilnosti, funkcije, vrste

In končno imamo množični tok 'j', ki prečka prečno območje membrane ali kanal, kjer se delci širijo. Če združimo te pogoje, se je rodila enačba Fickovega prvega zakona:

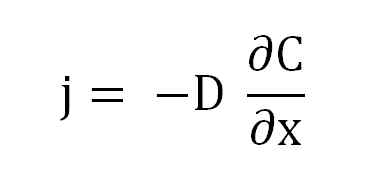Enačba Fickovega prvega zakona. Vir: Gabriel Bolívar.

Kjer je j sorazmerna z d in a (∂c/∂x), koncentracijski gradient.

Interpretacija in enote

Negativni simbol v enačbi služi nevtralizaciji negativnega znaka koncentracijskega gradienta. V nasprotnem primeru bi imel j negativno vrednost, ki je nenarejena. Prav tako je vrednost d pozitivna, tako da z množenjem z negativnim znakom, ki je pred njim, daje negativno vrednost.

Fickov prvi zakon označuje naslednje: večji kot je koncentracijski gradient (∂c/∂x), večji je masni tok j. To pomeni razlika med c₂ in c₁ Postane večja in zato se bo skozi membrano širilo več delcev.

Po drugi strani je J odvisen tudi od D, kar je odvisno od parametrov, kot so temperatura, viskoznost, molekulska teža in prečno območje do:

D ∝ (a/l) (s/√m_W)

Kjer je S topnost delca, ki se širi z okoljem, in m_W Njegova molekulska teža.

Glede enot komponent ali pogojev enačbe imamo:

-C (kg · m^-3 ali mol · m^-3)

-D (m^-2· S^-1)

-J (kg · m^-2· S^-1 ali mol · m^-2· S^-1)

Neto srednji kvadratni premik

Med razširjanjem se delci trčijo med seboj in po kratkih časovnih intervalih na koncu prevozijo ogromne razdalje Δx. Vendar pa ima lahko ΔX odvisno od pomena teh premikov negativne ali pozitivne vrednosti (glede na točko izvora). Zato se povprečje vrednosti Δx za vse molekule nagiba k 0.

Po drugi strani so vrednosti ΔX zelo majhne v primerjavi z razdaljami, ki tečejo delce. Ko trčijo, izgubijo mobilnost proti smeri, posledično pa imajo omejen neto premik; Na primer, 2 cm vnaprej v eno smer po potovanju na stotine metrov v trkih in skokih.

Einstein leta 1905 je našel matematični izraz za povprečno drsenje premika (torej drugačen od 0):

<(Δx)²> = 2dt

Določitev

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms To je povprečni neto kvadratni premik zadevnih delcev. (Δx)_Rms Pove nam, koliko delcev se v povprečju premika (v pozitivni ali negativni smeri). Nekateri delci se premikajo dalje ali najbližje razdalje kot (Δx)_Rms, povzroča Gaussovo porazdelitev.

Vam lahko služi: kalcijev oksid (CAO)

Fick drugi zakon

Enačba

Fickov prvi zakon opisuje difuzijo v stacionarnih pogojih, to je, da se množični tok J sčasoma ne razlikuje. V resničnih sistemih pa imamo nestacionarne pogoje, kjer se masni pretok ne razlikuje le v prostoru, ampak tudi sčasoma. Zato ga zanima določitev (∂c/∂t).

Spodaj imamo dve enačbi, ki predstavljata Fickov drugi zakon:

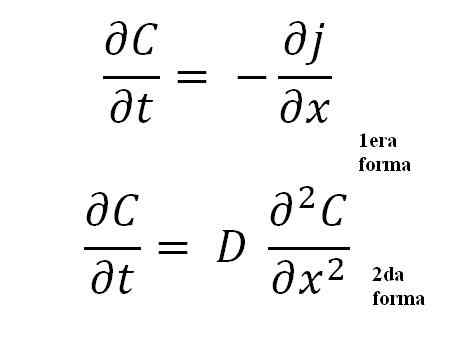Enačbe Fickovega drugega zakona. Vir: Gabriel Bolívar.

Druga oblika je najpomembnejša od vseh, saj predstavlja splošno matematično enačbo za vsak postopek razširjanja; Bodisi toplotni, električni, atomski itd.

Odbitek

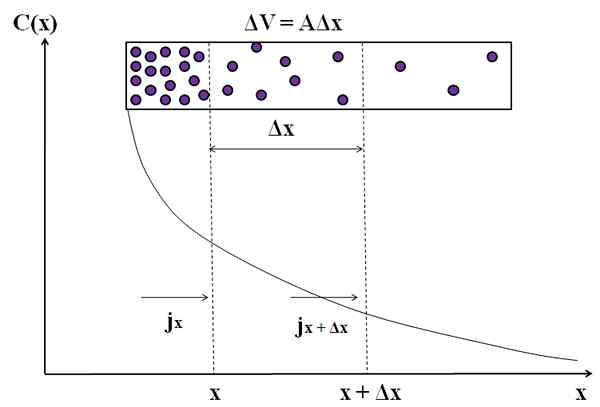Grafični prikaz, kako masni tok ni konstanten pri razširjanju teh molekul. Vir: Gabriel Bolívar.

Ponovno razmislite o vijolični delci v pravokotni komori. Med razdaljami x in x+Δx imamo tok j_x (dohodni) in j_x+Δx (odhajajoči). Glasnost kamere med temi razdaljami je opredeljena z:

ΔV = aΔx

Upoštevajte, da graf C (x) vs x ne izvira iz ravne črte, zato imamo različne vrednosti J (J_x ≠ j_x+Δx). Določiti moramo ΔC/ΔT.

Masa m_x Enako bo:

m_x = J_x AΔT

Dimenzijska analiza pomaga razumeti, zakaj:

kg = (kg · m^-2· S^-1) (m²) (S)

Na enak način izračunamo m_x+Δx:

m_{x+ Δx} = J_x+Δx AΔT

Je masa, ki se nabira v tej regiji, enaka ΔM:

Δm = m_x - m_{x+ Δx}

= (j_x - J_{x+ Δx}) AΔT

= -(J_{x+ Δx} - J_x) AΔT

= -ΔJAΔT

In vedeti, da je ΔC = ΔM/ΔV

ΔC = -ΔJAΔT/ ΔV

= -ΔJAΔT /AΔx

= -ΔJΔT/Δx

Očistimo ΔC/ΔT

ΔC/ΔT = -ΔJ/Δx

Ta izraz kaže, da je variacija koncentracije skozi čas enaka spreminjanju pretoka J glede na njegovo premik. Če uporabimo meje za ΔT in ΔX, ki se nanaša na 0, dobimo enak izraz kot delni derivat:

∂c/∂t = -(∂J/∂x) (1. obrazec)

Končno je drugi obrazec pridobljen z zamenjavo j s Fickovim prvim zakonom:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2. obrazec)

Rešene vaje

V naslednjih vajah bodo upoštevani zelo preprosti sistemi, katerih neznanke je mogoče rešiti s prvim zakonom Fick.

Vaja 1

Izjava

V cevi, dolgi 15 metrov in široki 21 centimetrov, ki je tudi nasičena z dušikom, se kisik tok razširi z enega konca na drugega pri temperaturi 0 ° C. Vedoč, da je pritisk na levi strani (P₁) je 20 kg/m³, In da pritisk na desno stran (P₂) je 10 kg, določite:

Lahko vam služi: Hydronio Ion

a) masni tok, ki se širi

b) Koliko kilogramov oz₂ Skozi cev se bodo razširili čez 17 minut?

c) koncentracijski gradient ali tlaki

d) pritisk o₂ na razdalji 7 metrov od vhoda v cevovod

e) Koliko bo 80 kg O₂ pri širjenju po tej cevi?

Upoštevajte, da je d_O2-N2 je enak 1.8 · 10^-5 m²· S^-1.

Resolucija

Iz Fickovega prvega zakona moramo rešiti pododdelek a):

J = -d (str₂-Str₁)/L

= -(1.8 · 10^-5 m²· S^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2· S^-1

Do b) Potrebujemo območje cevi:

A = π (0.21 m)²

= 0.14 m²

In pomnožimo j s časom T, da določimo maso ali₂ Prevzeto:

m_O2 = (1.2 · 10^-5 kg · m^-2· S^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Zdaj za pododdelek c) imamo, da je gradient enak:

Gradient = (str₂-Str₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Toda vzamemo pozitivno vrednost, kar je fizično smiselno:

2/3 (kg/m³) · M^-1

Ta vrednost nam bo nato služila za reševanje pododdelka D), če se gradient dobro razlaga: vsak meter tlak ali₂ 2/3 kg/m bo padlo³. S širjenjem 7 metrov bomo imeli:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 ali 4.7 kg/m³

To pomeni, da bo pritisk na tej razdalji:

(20-4.7) (kg/m³) = 15.3 kg/m³

In končno, pododdelek e) je podoben b), le da zdaj očistimo čas in ne mase:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2· S^-1) (0.14 m²)

= 47619.04 s ali 0.55 dan

Vaja 2

Izjava

Določite (Δx)_Rms Za saharozo v vodi pri t = 1 min, 1 h in 1 dan. Koeficient razširjanja saharoze v vodi je 0.52 · 10^-5cm²· S^-1.

Resolucija

Uporabljamo enačbo:

(Δx)_Rms ≡ <(Δx)²>^1/2 = (2dt)^1/2

Ocenjujemo (Δx)_Rms S časi, izraženimi v nekaj sekundah. Za t = 1 min ali 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (60s))^1/2

= 0.025 cm

Za t = 1 h ali 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (3600s))^1/2

= 0.19 cm

In končno za t = 1 dan ali 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5cm²· S^-1) (86400s))^1/2

= 0.95 cm

Upoštevajte, da s časom molekule saharoze sploh niso mogle premakniti 1 cm v nobeni smeri.

Reference

1. Walter J. Moore. (1963). Fizikalna kemija. V kemični kinetiki. Četrta izdaja, Longmans.
2. Iran. Levine. (2009). Načela fizikalnokemije. Šesta izdaja. MC Graw Hill.
3. Uvod v znanost o materialih in inženiring. (11. marec 2018). Fickov drugi zakon. Prof. Rajesh Prasad. [Video]. Obnovil od: YouTube.com
4. Wikipedija. (2020). Fickovi zakoni difuzije. Pridobljeno iz: v.Wikipedija.org
5. Laura Dickson. (10. septembra 2020). Difuzija. Kemija librettexts. Okrevano od: kem.Librettexts.org
6. Larissa Zhou et al. (1. september 2015). Razumevanje teorije difuzije in Fick -ovega zakona s hrano in kuhanjem. Ameriško fiziološko društvo. doi.org/10.1152/Advan.00133.2014