Homologne strani

Pojasnjujemo, kakšne so homologne strani, s primeri in vajami, rešenimi

Kaj so homologne strani?

The homologne strani V dveh ravnih geometrijskih številkah so tiste, ki medsebojno ustrezajo, ohranjajo podobnost. Na primer, desna roka osebe je homologna z desno roko druge osebe.

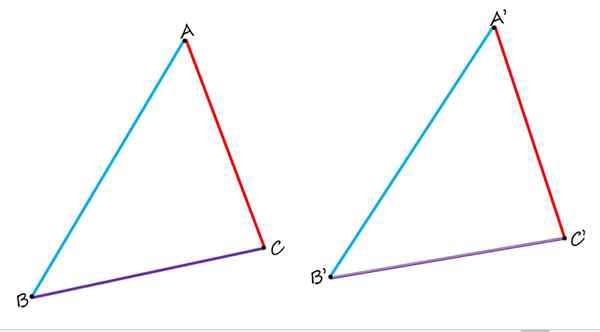
V ravni geometriji niso samo homologne strani, temveč tudi točki in homologni zorni koti. Če želite videti, razmislite o naslednji številki, ki jo sestavljata dva enaka trikotnika ABC in A'B'C ':

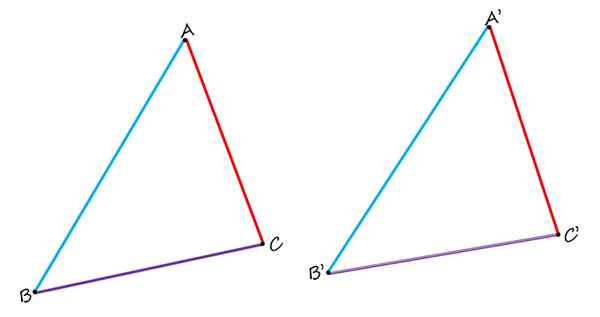V obeh enakih trikotnikih sta AB in A'B 'homologna, pa tudi strani BC in B'C' in AC in A'C '. Vir: f. Zapata.

Pri primerjavi jih jasno opazimo, da sta strani AB in A'B 'v modri barvi homologni, saj zavzemata podoben položaj v vsakem trikotniku. Strani BC in B'C 'v vijolični so tudi homologni. In končno je rdeča AC stran homologna na strani A'C '.

Pojasnilo

Iz zgoraj omenjenega izhaja, da so homologne strani tiste, ki na enak način zasedajo enak relativni položaj na številkah. Na prejšnji sliki sta bila za prikaz ideje uporabljena dva enaka trikotnika, vendar to zlahka posplošuje druge ravne geometrijske figure, ki jih tvorijo zaporedne strani, ki se zapirajo.

Te številke se imenujejo poligoni. Na primer, trikotniki in štirikotniki so poligoni 3 oziroma 4 strani.

Koncept homolognih strani je pomemben, ker omogoča določitev kriterijev podobnosti med poligoni, kot bomo kmalu videli. Podobne številke imajo popolnoma enako obliko in ohranjajo enak delež med svojimi stranicami, tudi če niso enake velikosti.

In čeprav so se do zdaj sklicevali le na ravne številke, obstajajo tudi podobne številke v treh dimenzijah. Zlahka jih opazimo na policah supermarketov, ko se isti izdelek prodaja v enakih posodah, vendar z drugačno velikostjo.

Vam lahko služi: matematična logika

Druge besede, ki se v geometriji zamenjujejo, da se v geometrijskih številkah nanašajo na homologne strani, so: ustrezne strani, ustrezne strani in enakovredne strani.

Homologne točke in koti

Tako kot na straneh so opredeljene tudi homologne točke, ki združujejo pare homolognih strani. Na primer, točki A in 'iz prejšnje številke so homologne. Podobno so pari vrhov B in B 'in C in C' homologni.

Končno homologni koti zavzemajo enak relativni položaj na slikah. Vrtice homolognih kotov so homologne.

Za ponazoritev ideje vzemite kot med modrimi in vijoličnimi stranicami levega trikotnika, ki ga je mogoče označiti kot ∠abc. Ta kot ima svoj kolega pod kotom ∠a'b'c ', od trikotnika na desno.

Vrh tega kota je B, ki je, kot je bilo že navedeno, protipostavka z B ', druga dva para homolognih kotov prikazanih trikotnikov pa sta:

• ∠bca in ∠b'c'a '
• ∠cab in ∠c'a'b '

Podobnost poligonov

Da bi bili podobni dvema poligonama, je treba izpolniti naslednje pogoje:

• Vsi pari homolognih kotov imajo enak ukrep
• Njegovi pari homolognih strani so sorazmerni.

Oba pogoja je treba izpolnjevati hkrati, da se zagotovi podobnost. Takoj opazimo, zakaj.

Na naslednji sliki obstajata dva kvadrilaterate, ki očitno nista podobna. To je posledica dejstva, da je prvi tedenski status izpolnjen, drugi pa ne:

Dva štirikotnika, ki si nista podobna, čeprav imata njihovi homologni koti enake mere. Vir: f. Zapata.

Medtem ko imajo njihovi pari homolognih kotov enak ukrep, ker so vsi ravni koti (merijo 90 °), številke niso podobne, ker njihovi pari strani niso sorazmerni.

Vam lahko služi: injektivna funkcija: iz česa je sestavljena, kaj je in primeri

Po drugi strani pa imata ta dva štirikolesnik homologne strani z enako mero, vendar homologni koti ne merijo istega. Zato številke očitno niso podobne.

Dva štirikotnika s homolognimi stranicami istega ukrepa, vendar z različnimi notranjimi koti, zato nista podobni številki. Vir: f. Zapata.

Razlog podobnosti

Če sta dve številki podobni, je količnik med homolognimi stranicami enak in se imenuje Razlog podobnosti.

Označevanje strani ene od figur, kot so A, B, C, D ... in ustreznih drugih figur kot A ', B', C ', D

Obod in območja podobnih številk

Razmerje podobnosti omogoča pridobivanje odnosov med obodnimi, območji in količino dveh podobnih številk.

Obodni razlog za dve podobni številki

Obod P poligona je opredeljen kot vsota vseh strani. Če imate figuro, katere stranice so ', b', c ', d' ..., je njegov obod p ':

P '= a' + b ' + c' + d '.. .

Če je to podoben drugemu poligonu in so njene strani A, B, C, D ..., je izpolnjeno:

In zato:

A = r ∙ a '

Enako lahko potrdite za druge strani te številke. Torej je obod P izražen kot:

P = a + b + c + d .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Ker je "R" pogost dejavnik za vse odvisnike, je odnos med P in P ':

P = r ∙ p '

To pomeni, da je razlog za obode med dvema podobnima poligonama enak razlogi za podobnost.

Razlog za območja dveh podobnih številk

Če imata dve podobni številki območja A in A ', so ta povezana z:

Vam lahko služi: vaje za čiščenje formule

A = r²∙ a '

Kjer je "r" razlog za podobnost številk.

Količinsko razmerje dveh podobnih številk

To sta dve podobni tridimenzionalni figuri, katerih količine so v in v '. Odnos med njimi je prek "R":

V = r³∙ V '

Primeri

Načrti

Deli zemlje, obrat stavbe ali celo oblačila, v manjšem obsegu na listu papirja so lahko predstavljeni. Načrti imajo prednost, da se lahko s seboj vzamejo in spreminjajo ustrezne modifikacije, preden se uresničijo na resničnem predmetu.

Zemljevidi

Običajno so reprezentacije v ravnini velikega območja zemlje, od vasi do celin. Izdelani so tudi v določenem obsegu.

Imajo številne aplikacije in obstaja veliko vrst. Na primer, prek zemljevida je mogoče opisati teren in ko se nahaja na določeni točki, je določena najboljša pot od te točke do druge.

Modeli

So tridimenzionalne predstavitve na lestvici predmetov, kot so avtomobili, zgradbe in konstrukcije na splošno.

Vaja rešena

Naslednje vrednosti ustrezajo strani nekaj podobnih trikotnikov. Poiščite razlog za podobnost in vrednosti "x" in "y":

Trikotnik 1: 5, 8, 10

Trikotnik 2: 150, x, y

Rešitev

Razlog za podobnost je količnik:

R = 150/5 = 30

Zato:

x = 30 × 8 = 240

y = 10 × 30 = 300