Demonstracija pitagorejske identitete, primer, vaje

So Pitagorejske identitete Vse trigonometrične enačbe, ki so izpolnjene za katero koli vrednost kota in temeljijo na izrek Pitagore. Najbolj znana pitagorejska identiteta je temeljna trigonometrična identiteta:

Sen²(α) + cos²(α) = 1

Slika 1. Pitagorejske trigonometrične identitete.

Še vedno je pomembna in uporablja pitagorejsko identiteto tangenta in secanta:

Tako²(α) + 1 = sek²(α)

In pitagorejsko trigonometrično identiteto, ki vključuje kotangent in kombajn:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstracija

Trigonometrični razlogi prsi in kosinus Zastopani so v obodu polmera ena (1), znana kot trigonometrični krog. Ta krog ima središče pri izvoru koordinat oz.

Koti se merijo iz pozitivne polkise X, na primer kot α na sliki 2 (glej kasneje). V nasprotju z rokami ure, če je kot pozitiven, in v smeri rok, če je negativen kot.

Narisana je polčas z izvorom ali in kotom α, ki prestreže krog enote v točki P. Točka P se projicira pravokotno na vodoravni osi x, kar povzroči točko C. Podobno je P pravokotno projiciran na navpični osi in sproži točke S.

Imate pravi trikotnik OCP v C. 

Dojke in kosinus

Ne pozabite, da trigonometrični razlog prsi Na desnem trikotniku je opredeljen na naslednji način:

Natiček kota trikotnika je razmerje ali razmerje med kateto, ki nasprotuje kot in hipotenuzo trikotnika.

Uporablja se na trikotniku OCP slike 2, kot je ta:

Sin (α) = cp / op

Toda CP = OS in OP = 1, tako da:

Sin (α) = OS

Kar pomeni, da ima projekcija na osi y vrednost, ki je enaka krogu prikazanega kota. Treba je opozoriti, da se največja vrednost prsi kota (+1) pojavi, ko je α = 90 ° in najmanj (-1), ko je α = -90 ° ali α = 270 °.

Vam lahko služi: vektorski prostor: baza in dimenzija, aksiomi, lastnosti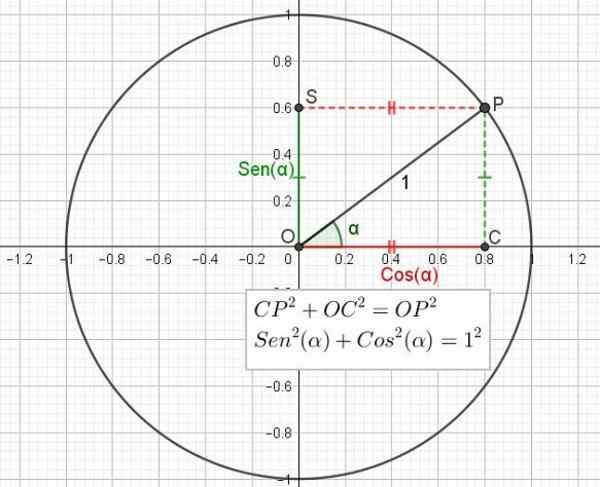Slika 2. Trigonometrični krog, ki prikazuje razmerje med teoremom pitagore in temeljno trigonometrično identiteto. (Lastna izdelava)

Podobno je kosinus kota razmerje med kategorijo, ki meji na kota, in hipotenuzo trikotnika.

Uporablja se na trikotniku OCP slike 2, kot je ta:

Cos (α) = oc / op

Ampak op = 1, tako da:

Cos (α) = oc

Kar pomeni, da ima projekcija OC na osi x vrednost, ki je enaka vrednosti prikazanega kota. Treba je opozoriti, da se največja vrednost kosinusa (+1) pojavi, kadar je α = 0 ° ali α = 360 °, medtem ko je najmanjša vrednost kosinusa (-1), ko je α = 180 °.

Temeljna identiteta

Za pravokotnik OCP trikotnik se uporablja teorem pitagore, ki navaja, da je vsota kvadrata kategorij enaka kvadratu hipotenuze:

Cp² + Oc² = OP²

Toda že je bilo rečeno, da je cp = OS = sin (α), da je oc = cos (α) in da je op = 1, tako da je mogoče prejšnji izraz napisati, odvisno od sinusa in kosina kota:

Sen²(α) + cos²(α) = 1

Os tangenta

Tako kot os x v trigonometričnem krogu je os kosinusa in os in osi dojke, na enak način je osi tangenta (glej sliko 3), ki je natančno črta, tangentna do enote krog na točki na koordinatu točke B (1, 0). 

Če želite vedeti vrednost tangenta kota, se kot izvleče iz pozitivnega poltoka x je tangenta kota.

Vam lahko služi: algebrski derivati

To je zato, ker je po definiciji tangent kota α nasprotni Cateto QB med sosednjim catetom OB. To pomeni, da je tako (α) = qb / ob = qb / 1 = qb.

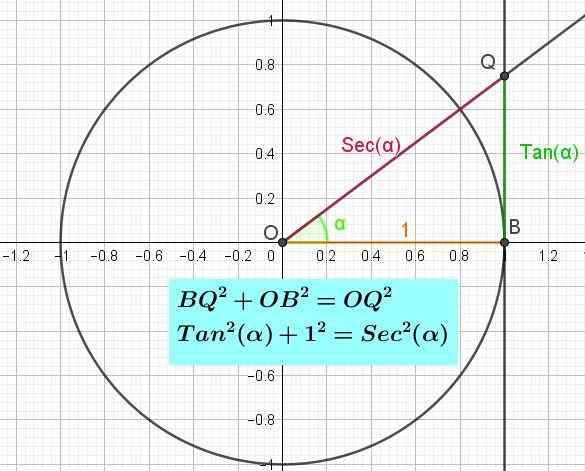Slika 3. Trigonometrični krog, ki prikazuje os tangenta in pitagorejske identitete tangenta. (Lastna izdelava)

Pitagorejska identiteta tangenta

Pitagorejsko identiteto tangenta je mogoče dokazati, če se upošteva trikotnik pravokotnika v B (slika 3) (slika 3). Uporaba teorema pitagore za omenjeni trikotnik morate BQ² + OB² = OQ². Toda že je bilo rečeno, da je BQ = tan (α), da je OB = 1 in da je OQ = sec (α), tako da je nadomeščanje enakosti pitagore za pravi trikotnik OBQ

Tako²(α) + 1 = sek²(α).

Primer

Preverite, ali so v pravokotni trikotnik Catetos AB = 4 in Bc = 3 izpolnjene pitagorejske identitete ali ne.

Rešitev: Kategorije so znane, treba je določiti hipotenuzo, ki je:

AC = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Kot ∡Bac se imenuje α, ∡Bac = α. Zdaj so določeni trigonometrični razlogi:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

Sec α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Začne se s temeljno trigonometrično identiteto:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Sklepano je, da je izpolnjen.

- Naslednja pitagorejska identiteta je Tangenta:

Tako²(α) + 1 = sek²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

In sklenjeno je, da je identiteta tangenta preverjena.

- Podobno kot kotangenta:

Vam lahko služi: naključne izbire z ali brez zamenjave

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Ugotovljeno je, da je tudi izpolnjena, kar je dokončalo nalogo preverjanja pitagorejskih identitet za dani trikotnik.

Rešene vaje

Preizkusite naslednje identitete, ki temeljijo na definicijah trigonometričnih razlogov in pitagorične identitete.

Vaja 1

Dokažite, kaj cos² x = (1 + sen x) (1 - sin x).

Rešitev: Desni član prepozna opazen produkt množenja binoma s svojim konjugatom, ki je, kot je znano, razlika kvadratov:

Cos² x = 1² - Sen² x

Nato izraz z dojki na desni strani preide na levo stran s spremenjenim znakom:

Cos² X + sen² x = 1

Ob upoštevanju, da je bila dosežena temeljna trigonometrična identiteta, zato je ugotovljeno, da je dani izraz identiteta, torej izpolnjena za katero koli vrednost x.

Vaja 2

Začenši iz temeljne trigonometrične identitete in z uporabo definicij trigonometričnih razlogov za prikaz pitagorejske identitete kombajna.

Rešitev: Temeljna identiteta je:

Sen²(x) + cos²(x) = 1

Oba člana sta razdeljena med SEN²(x) in imenovalec je razdeljen v prvem članu:

Sen²(x)/greh²(x) + cos²(x)/greh²(x) = 1/sen²(x)

Poenostavljeno je:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) je identiteta (ne -pitagorejsko), ki je preverjena z opredelitvijo trigonometričnih razlogov. Na enak način se zgodi z naslednjo identiteto: 1/sin (x) = csc (x).

Končno moraš:

1 + CTG²(x) = csc²(x)

Reference

1. Baldor J. (1973). Ravna geometrija in prostor z uvodom v trigonometrijo. Srednjeameriška kulturna. C.Do.
2. C. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
3. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Uredniška skupina Patria.
4. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.
5. Jr. Geometrija. (2014). Poligoni. Lulu Press, Inc.
6. Miller, Heeren in Hornsby. (2006). Matematika: sklepanje in aplikacije (deseta izdaja). Pearson Education.
7. Patiño, m. (2006). Matematika 5. Uredništvo Progreso.
8. Wikipedija. Trigonometrična identiteta in formule. Okrevano od: je.Wikipedija.com