Matematika

Hiperbola

1235
109
Raymond Moen

Kaj je hiperbola?

Hiperbola je niz točk ravnine, tako da absolutna vrednost razlike med razdaljami na dve fiksni točki, imenovana Spotlights, ostane konstantna. Ta niz točk tvori krivuljo z dvema vejama, prikazani na sliki 1.

Obstaja točka p (x, y), žarišča f₁ in f₂ ločena razdalja, enaka 2C. Matematični način izražanja tega odnosa je skozi:

$\left |d__P_1-d__P_2 \right |=constante$

Slika 1. Hiperbola z vodoravno žariščno osjo. Vir: f. Zapata.

Vse točke hiperbole izpolnjujejo to stanje, kar vodi do enačbe hiperbole, kot bo razvidno pozneje. Srednja točka med osvetlitvami se imenuje Center C, na sliki pa sovpada s točko (0,0), vendar lahko hiperbola tudi premestimo in njegovo središče ustreza drugi koordinatni točki C (H, K).

Na zgornji sliki je os x žariščna os hiperbole, saj obstajajo osvetlitve, lahko pa sestavite tudi tisto, katerega žariščna os je os in os os.

Hiperbola je del krivulj, znanih kot stožčasto, To se imenujejo, ker jih je mogoče izrezati iz reza stožca z ravnim odsekom. Hiperbola dobimo pri sekanju stožca in ravnine, pod pogojem, da ne prehaja skozi vrhovo stožca in kota, ki tvori ravnino z osjo stožca, je manjša od tiste enako.

Skupaj s prispodobo, obodom in elipso so koniki znani že od antičnih časov. Grški matematik Apolonij iz Perge (262-190 pr.n.št.

Značilnosti hiperbole

To je nekaj najbolj izjemnih značilnosti hiperbole:

To je ravno krivulja, zato je dovolj, da koordinate (x, y) daste vsake točke, ki ji pripada.
Je tudi odprta krivulja, za razliko od oboda ali elipse.
Ima simetrično dve veji.
Tako navpična os kot vodoravna osi lahko obravnavamo kot simetrične osi, vendar osi, kjer se imenujejo osvetlitve žariščna osi ali glavna os.
Je simetričen glede na njegovo središče.
Hiperbola seka žariščna osi na dveh točkah, imenovanih Točke, Zato se včasih imenuje žariščna os prava os, Medtem ko se imenuje druga os Namišljena os, Ker nima skupnih točk s hiperbolo.
Središče hiperbole se nahaja na polovici poti med točkami, imenovanimi FOCI.
Povezana je z dvema zelo določenima vrsticama, imenovanima asimptoti, ki so črte, do katerih se bliža hiperbola, vendar brez prekrižanja, ko so vrednosti x e y zelo velike. Asimptote se sekajo v središču hiperbole.

Lahko vam služi: Prevelika funkcija: definicija, lastnosti, primeri

Enačbe in formule

Enačba hiperbola s središčem v (0,0)

Začenši z definicijo, podano na začetku:

$\left |d__P_1-d__P_2 \right |=constante$

Na to pozitivno konstanto se običajno imenuje 2A in razdalja loči točke hiperbole, nato pa:

$\left |d__P_1-d__P_2 \right |=2a$

Po drugi strani pa dp₁, Dp₂ in 2C sta strani trikotnika, prikazani na sliki 1, in po osnovni geometriji je odštevanje kvadratov strani katerega koli trikotnika vedno manjše od kvadrata preostale strani. Tako:

4²< 4c²

In:

do < c

Ta rezultat bo v kratkem koristen.

Kot razdalja med dvema točkama p₁(x₁,in₁) In p₂(x₂,in₂) je:

$d_12=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$

Z zamenjavo koordinat p (x, y), f₁(-C, 0) in f₂(C, 0) Ostaja:

$\left |d_P_1-d_P_2 \right |=\left |\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2 \right |=2a$

Ki je enakovredno:

$\sqrt(x+c)^2+(y-0)^2-\sqrt(x-c)^2+(y-0)^2=\pm 2a$

Kvadrate v obeh članih, da odpravite korenine in reorganizirajo izraze, ki jih dosežete:

$\left (c^2-a^2 \right )x^2-a^2 y^2 =\left (c^2-a^2 \right )a^2$

Do količine c² - do², kar je vedno pozitiven znesek < c, se la denomina b², Zato je zgoraj napisano kot:

b²x² - do²in² = a² b²

Delitev vseh izrazov² b², To je enačba hiperbole, osredotočena na (0,0) z vodoravno realno osi:

$\fracx^2a^^2-\fracy^2b^^2=1$

Z A in B večjo od 0. Ta enačba se imenuje Hyerbola kanonična enačba in imenovalec² Vedno ustreza pozitivni frakciji.

Hyperbola je bila osredotočena na (0,0) in z navpično resnično osi je v obliki:

$\fracy^^2a^2-\fracx^^2b^2=1$ Križišča hiperbole s koordinatnimi osi

V enačbi se križišča hiperbole s koordinatnimi osi izvajajo y = 0 in x = 0:

Za y = 0

x² /do² = 1 ⇒ x² = a²

x = ± a

Hiperbola se v dveh točkah, imenovanih točkah, reže na osi x, katerih koordinate x so: x = a y x = -a

Za x = 0

Pridobljeno je -in² /b² = 1, ki nima prave rešitve in sledi, da se hiperbola ne razreže na navpično osi.

Enačba hiperbole s centrom v (h, k)

Če je središče hiperbole v točki C (h, k), potem je njegova kanonična enačba:

$\frac\left (x-h \right )^2a^^2-\frac\left (y-k \right )^2b^^2=1$

Elementi hiperbole

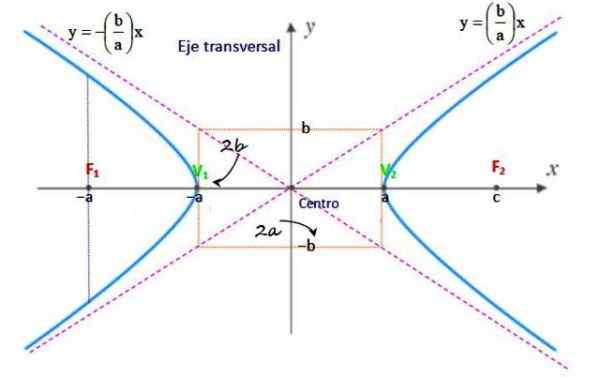Slika 2. Elementi hiperbole. Vir: f. Zapata.

Center

Je sredi točke segmenta f₁F₂In njegove koordinate so (h, k) ali (x_tudi,in_tudi).

Vam lahko služi: sintetična delitev

Focos

Sta dve fiksni točki F₁ in f₂ ki so na resnični osi hiperbole, glede na to, da razlika razdalj do točke P (x, y) ostane konstantna. Razdalja med reflektorji in sredino hiperbole je "C".

Vektorski radio

To se imenuje razdalja med točko P in enim od osvetlitve.

Goriščna razdalja

Razdalja loči oba osvetlitve in je enakovredna 2C.

Točke

Vrtice v₁ in v₂ To so točke, kjer hiperbola seka resnično osi. Vertex in središče hiperbole sta ločena z razdaljo A, zato je razdalja med točkami 2a.

Žariščna os, glavna osi ali resnična os

To je os, kjer se nahajajo osvetlitve in meri 2C. Nahaja se lahko na kateri koli od dveh kartezijanskih osi in hiperbola jo seka na točkah, imenovanih točkah.

Prečna os, sekundarna os ali namišljena os

Os je pravokotna na žariščno os in meri 2b. Hiperbola je ne seka, zato se imenuje tudi namišljena os.

Asimptote

Sta dve vrstici, katerih v teku sta M₁ = (b/a) in m₂ = - (b/a), ki so namenjeni v središču hiperbole. Krivulja nikoli ne seka teh linij in izdelka med razdaljami katere koli točke hiperbole na asimptote, konstantna je.

Če želite najti enačbe asimptotov, se le ujemajte z levo stranjo kanonične enačbe hiperbole na 0. Na primer, za hiperbolo, osredotočeno na izvor:

$\fracx^^2a^2-\fracy^^2b^2=0\Rightarrow \fracy^^2b^2=\fracx^^2a^2$

Hyberbola pravokotnik

To je pravokotnik, katerega širina je razdalja med vrhovi 2a in razdaljo 2b in je osredotočena na središče hiperbole. Njegova konstrukcija olajša ročno postavitev hiperbole.

Ravna stran

Vrv, ki poteka skozi eno od osvetlitve, pravokotno na pravo osi.

Ekscentričnost

Opredeljen je kot količnik med goriščno razdaljo in resnično osi:

E = c/a

Vedno je večji od 1, saj je C večji od A in manj kot √2.

Vrednost in označuje, ali je hiperbola precej zaprta (ozek pravokotnik, podolgovat v smeri glavne osi) ali odprta (širok pravokotnik, podolgovat v smeri namišljene osi).

Ravna tangenta do hiperbole v točki P (x₁,in₁)

Tangentna črta do hiperbole na točki P (x₁,in₁) Je bisektor obeh radijskih vektorjev te točke.

Za hiperbolo z glavno osi, vzporedno z osi x, naklon črte tangenta do hiperbole v točki P (x₁,in₁) daje:

Vam lahko služi: kombinirane operacije

$m=\left (\fracba \right )^2\left (\fracx_1y_1 \right )$

In če je hiperbola glavna os vzporedna z osi y, potem:

$m=\left (\fracab \right )^2\left (\fracx_1y_1 \right )$

Primeri hiperbole

Disperzija alfa delcev z jedrom

Z bombardiranjem atomskih jeder z alfa delci, ki niso nič drugega kot jedra helija, so to odvržene, saj ima katero koli atomsko jedro pozitiven naboj. Ta helijeva jedra so razpršena po hiperboličnih usmeritvah.

Usmeritve teles sončnega sistema

Slika 3: Planeti sončnega sistema

V sončnem sistemu se predmeti premikajo pod delovanjem sile gravitacije. Opis gibanja izhaja iz diferencialne enačbe, v kateri je sila konzervativna in obratno sorazmerna s kvadratom razdalje. In rešitve te enačbe so možne usmeritve, ki sledijo predmetom.

No, te poti so vedno stožčaste: okolice, elipse, prispodobe ali hiperbole. Prva dva sta zaprta krivulja in tako se premikajo planeti, nekateri kometi pa so še vedno odprte usmeritve, kot so prispodobe ali hiperbole, s soncem, ki se nahaja v enem od osvetlitve.

Minimalni zvok

Ko obstajata dva zvočna vira, kot sta dva zvočnika, ki oddajata enakomerno v vseh smereh, ki se nahajajo vzdolž ravne črte, so najmanj intenzivnosti zvoka (uničevalne motnje) na hiperboli, katere glavna os je omenjena črta, in v središčih pozornosti hiperbola so govorci.

Vaja rešena

Poiščite elemente naslednje hiperbole: točke, žarišča in asimptote hiperbole in sestavite njegov graf:

$\fracx^^216-\fracy^^24=1$

Rešitev

Središče te hiperbole sovpada z izvorom koordinat in njena realna os je vodoravna, saj pozitivna frakcija ustreza spremenljivki x.

Polbola pol -osi so:

do² = 16 ⇒ a = 4

b² = 4 ⇒ b = 2

Na ta način centralni pravokotnik meri 4 enote in visoke 2 enoti. Spominjam se, da je bilo zgoraj omenjeno, da je C² - do²= b², tako:

c² = a²+ b² ⇒ c² = 16 + 4 = 20

Zato je osrednja pol-delnica:

C = √20 = 2√5

In žarišči so na koordinatnih točkah f₁ (-2√5.0) in f₂ (2√5.0).

Pobočja asimptotov so:

m = ± (b/a) = ± (2/4) = ± 0.5

Zato so ustrezne enačbe vsake:

in₁ = 0.5x; in₂ = -0.5x

Hyperbola lahko enostavno graficira prek spletne programske opreme, kot je Geogebra:

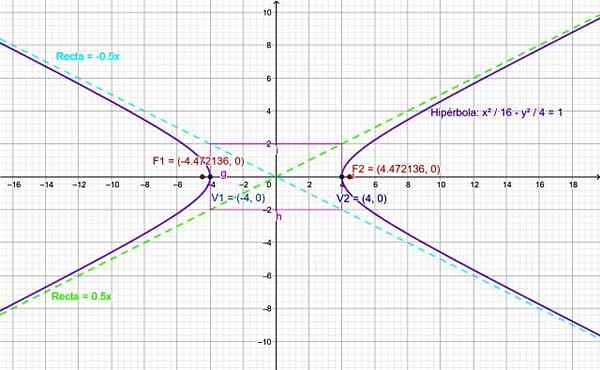Slika 4. Graf za hiperbolo vaje Rešena. Vir: f. Zapata.

Reference

FisicalAb. Enačba hiperbole. Okreval od: fisicalbab.com
Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
Formule vesolja. Hiperbola. Okrevano od: univerzeformulas.com
Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.

Hiperbola

Kaj je hiperbola?

Značilnosti hiperbole