Hypercubo definicija, dimenzije, koordinate, razgrnjene

A Hypercubo je dimenzija kocka n. Poseben primer dimenzije hipercubo se imenuje Testeract. Hypercubo ali N-kubo je sestavljen iz ravnih segmentov, vse iste dolžine, ki so pravokotni v svojih točkah.

Človeška bitja dojemajo tridimenzionalni prostor: širok, visok in globina, vendar nam ni mogoče vizualizirati hiperkubo dimenzije, večje od 3. 

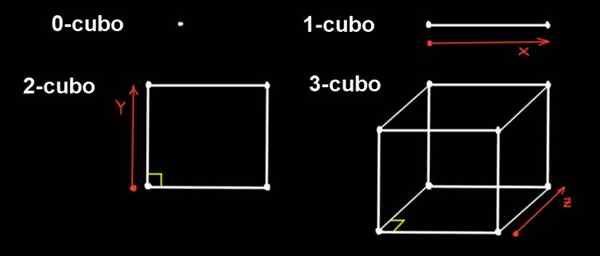
Slika 1. 0-kubo je točka, če se ta točka razprostira v eni smeri razdalje na način 1-kubo Če se 2-kubo razširi na razdaljo v pravokotni smeri, je 3-kubo. Vir: f. Zapata.

V treh dimenzionalnih prostorih lahko naredimo projekcije, da ga predstavljamo, podobno kot projiciramo kocko na ravnini, da jo predstavljamo.

V dimenziji 0 je edina številka točka, zato je 0-kubo točka. 1-kubo je raven segment, ki nastane s premikanjem točke na daljavo do.

Za svoj del je 2-kubo kvadrat. Zgrajena je z izpodrivanjem 1-kubo (segment dolge a) v smeri in, ki je pravokotna do naslova X, razdalja do.

3-kubo je običajna kocka. Zgrajena je iz kvadrata, ki je enaka v tretji smeri (z), ki je pravokotna v smeri x in y, razdalja do.

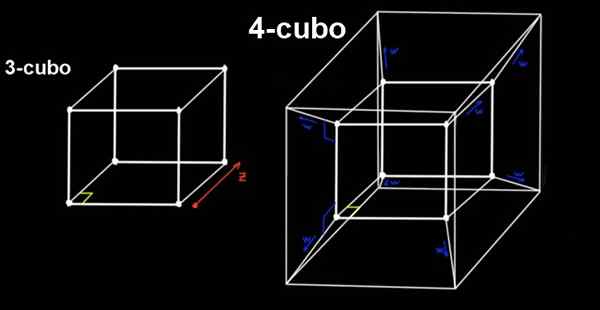Slika 2. 4-kubo (testeract) je razširitev 3-kubo v ortogonalni smeri na tri običajne prostorske naslove. Vir: f. Zapata.

4-kubo je preskus, ki je zgrajen iz 3-kubov, ki premika isto pravokotno, na daljavo do, proti četrti dimenziji (ali četrti smeri), ki je ne moremo zaznati.

Sprožilec ima vse svoje ravne kote, ima 16 vrhov in vsi robovi (skupaj 18) imajo enako dolžino do.

Če je dolžina robov N-kubo ali hipercubo dimenzije n.

Vam lahko služi: linearno programiranje: za kaj je, modeli, omejitve, aplikacijeSlika 3. N-kubo dobimo iz (N-1) -cubo, ki ga v naslednji dimenziji iztegne pravokotno. Vir: Wikimedia Commons.

[TOC]

Kakšne so dimenzije?

Dimenzije so stopnje svobode ali možne smeri, v katere se lahko premakne predmet.

V dimenziji 0 ni možnosti za premikanje in edini možni geometrijski objekt je točka.

Dimenzija v evklidskem prostoru je predstavljena z orientirano črto ali os, ki definira to dimenzijo, imenovano os x. Ločitev med dvema točkama A in B je evklidska razdalja:

D = √ [(x_do - x_b)²]. 

V dveh dimenzijah je prostor predstavljen z dvema pravokotnima usmerjenimi črtama drug z drugim, imenovanim x in osi.

Položaj katere koli točke v tem dvodimenzionalnem prostoru je podan s par kartezijanskimi koordinatami (x, y), razdalja med dvema točkama A in B pa bo:

D = √ [(x_do - x_b)² + (in_do - in_b)²]

Ker gre za prostor, kjer se izpolnjuje euclid geometrija.

Trijedimenzionalni prostor

Tri -dimenzionalni prostor je prostor, v katerem se premikamo. Ima tri navodila: širina, visoka in globina.

V prazni sobi si pravokotni kotički med seboj dajo te tri smeri in vsakemu lahko povežemo osi: x, y, z.

Ta prostor je tudi evklidski in razdalja med dvema točkama A in B se izračuna na naslednji način:

D = √ [(x_do - x_b)² + (in_do - in_b)² + (z_do - z_b)²]

Človeška bitja ne morejo zaznati več kot treh prostorskih dimenzij (ali Euclideas).

Vendar je s strogo matematičnega vidika mogoče.

V tem prostoru ima točka koordinate: (x1, x2, x3, ..., xn) in razdalja med dvema točkama je: 

D = √ [(x₁ - x_{1 b})² + (x_{2. mesto} - x_2B)² +... + (x_na - x_Nb)²].

Vam lahko služi: hipergeometrična porazdelitev: formule, enačbe, model

Četrta dimenzija in čas

Dejansko se v teoriji relativnega časa obravnava kot še ena dimenzija in koordinata je povezana.

Vendar je treba razjasniti, da je ta koordinata, povezana s časom. Zato ločitev dveh točk ali dogodkov v prostoru in času ni Euclidiana, ampak sledi metriki Lorentza.

Štiridimenzionalni hiperkubo (sprožilec) ne živi v vesolju in času, spada v štiridimenzionalni evklidealni hiper-prostor. 

Slika 4. 3D projekcija štiri -dimenzionalnega hiperkubo v preprostem vrtenju okoli ravnine, ki sprednjo figuro deli na levo, nazaj v desno in od zgoraj navzdol. Vir: Wikimedia Commons.

Koordinate hipercubo

Koordinate vrhov N-kubo, osredotočene na izvor, dosežejo z vsemi možnimi permutacijami naslednjega izraza:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Kjer je a dolžina roba.

-On glasnost Z roba roba A je: (a/2)ⁿ (2ⁿ) = aⁿ.

-The Najdaljša diagonala To je razdalja med nasprotnimi tolici.

-Naslednje so Nasproti točki na kvadratu: (-1, -1) in (+1, +1).

-In v a Kocka: (-1, -1, -1) in (+1, +1, +1). 

-The Najdaljša diagonala ukrepov N-kubo: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

V tem primeru se je domnevalo, da je stran a = 2. Za n-kubo bo ostala:

d = a√n.

-Preskus ima vsako od 16 vrhov, povezanih s štirimi robovi. Naslednja slika prikazuje, kako so vrhovi povezani v sprožilcu.

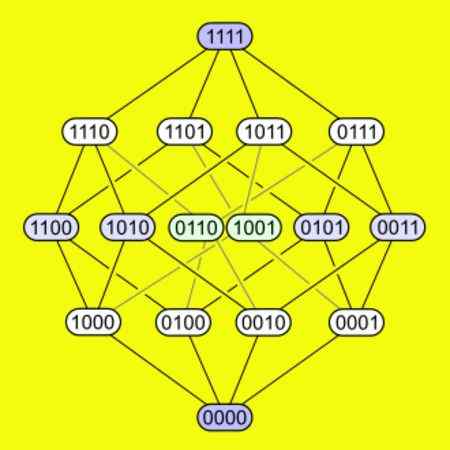Slika 5. Prikazanih je 16 vrhov štiri -dimenzionalnega hipercubo in kako povezujejo isto. Vir: Wikimedia Commons.

Razgrnjen hipercubo

Na redni geometrijski figuri, na primer poliedron, je mogoče razviti v več številkah nižje dimenzionalnosti.

V primeru 2-kubo (kvadrat) je mogoče razviti v štiri segmente, to je štiri 1-kubo.

Lahko vam služi: Poissonova distribucija: formule, enačbe, model, lastnosti

Podobno je mogoče 3-kubo razviti v šestih 2-kubo.

Slika 6. N-kubo je mogoče razviti v več (N-1) -Cubos. Vir: Wikimedia Commons.

4-kubo (testeract) je mogoče razviti v osmih 3-kubo.

Naslednja animacija prikazuje razplet trope.

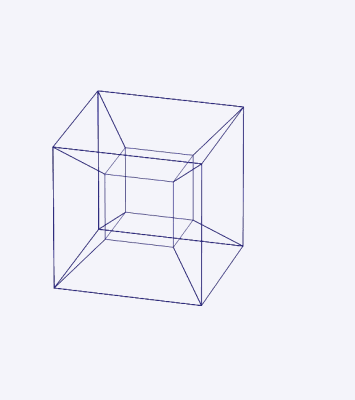Slika 7. 4 -dimenzionalni hiperkubo je mogoče razviti v osmih treh -dimenzionalnih kockah. Vir: Wikimedia Commons. Slika 8. Tri -dimenzionalna projekcija štiri -dimenzionalnega hipercubo, ki naredi dvojno vrtenje okoli dveh pravokotnih ravnin. Vir: Wikimedia Commons.

Reference

1. Znanstvena kultura. Hypercubo, ki vizualizira četrto dimenzijo. Pridobljeno iz: Culturacienta.com
2. Epsiloni. Tetradimenzionalni hipercubo ali tesseract. Okrevano od: epsiloni.com
3. Perez R, Aguilera a. Metoda za pridobitev preskusa iz razvoja hipercubo (4D). Okrevano od: Researchgate.mreža
4. Wikilibros. Matematika, poliedri, hiperkubes. Okrevano od: je.Wikibooks.org
5. Wikipedija.  Hiperkube. Pridobljeno iz: v.Wikipedija.com
6. Wikipedija. Tesseract. Pridobljeno iz: v.Wikipedija.com