Stopnja polinoma, kako je določena, primeri in vaje

On stopnja polinoma v a Spremenljivka je podana z izrazom, ki ga ima glavni eksponent, in če ima polinom Dve ali več spremenljivk, Potem je stopnja določena z vsoto eksponentov vsakega mandata, glavno vsoto polinoma.

Poglejmo, kako na praktičen način določiti stopnjo polinoma.

Slika 1. Znana Einsteinova enačba za energijo E je absolutni monom stopnje 1 za masno spremenljivko, označena z M, saj se hitrost svetlobe C šteje za konstantno. Vir: Piqsels.

Recimo, da je polinom p (x) = -5x + 8x³ + 7 - 4x². Ta polinom je spremenljivka, v tem primeru je spremenljivka x. Ta polinom je sestavljen iz več izrazov, ki so naslednji:

-5x; 8x³; 7; - 4x²

 Izberite med štirimi izrazi, katerih eksponent je večji, ta izraz je:

8x³

In zdaj, kaj je eksponent? Odgovor je 3. Zato je p (x) polinom stopnje 3 stopnje.

Če ima zadevni polinom več kot eno spremenljivko, potem je lahko stopnja:

-Absolutno

-V zvezi s spremenljivko

Absolutna stopnja je razložena na začetku: dodajanje eksponentov vsakega izraza in izbiro največjega.

Po drugi strani je stopnja polinoma glede na eno od spremenljivk ali črk največja vrednost eksponenta, ki je navedel pismo. Točka bo jasnejša s primeri in vajami, rešenimi iz naslednjih razdelkov.

[TOC]

Primeri stopnje polinoma

Polinome je mogoče razvrstiti po stopnji, saj so sposobni biti prve stopnje, drugega razreda, tretjega razreda in tako naprej. Za primer slike 1 je energija prvi -stopinjski monom za maso.

Vam lahko služi: skladnost: skladne številke, merila, primeri, vaje

Pomembno je tudi opaziti, da je število izrazov, ki jih ima polinom, enako stopnji plus 1. Tako:

-Polinomi prve stopnje imajo dva izraza: a₁x + a_tudi

-Drugi -stopinjski polinom ima 3 izraze: a₂x² + do₁x + a_tudi

-Polinom tretje stopnje ima 4 izraze: a₃x³ + do₂x² + do₁x + a_tudi

In tako naprej. Pozorni bralec bo opazil, da so polinomi prejšnjih primerov napisani na zmanjšanje, to je, da najprej postavite izraz z glavno stopnjo.

V naslednji tabeli se pojavljajo različni polinomi, tako iz ene kot več spremenljivk kot tudi njihovih absolutnih stopinj:

Tabela 1. Primeri polinomov in njihovih stopenj

Polinom	Stopinja
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
x5-bx4+Abx3+Ab3x2	6
3x3in5 + 5x2in4 - 7xy2 + 6	8

Zadnja dva polinoma imata več kot eno spremenljivko. Izraz, ki ima največjo absolutno stopnjo, je izstopal krepko, tako da bralec hitro preveri diplomo. Pomembno si je zapomniti, da kadar spremenljivka nima pisnega eksponenta, se razume, da je omenjeni eksponent enak 1.

Na primer v vidnem terminu Ab³x² Obstajajo tri spremenljivke, in sicer: do, b in x. V tem izrazu, do Je dvignjen na 1, to je:

a = a¹

Zato Ab³x² = a¹b³x²

Ker je eksponent B 3 in je X 2, takoj sledi, da je stopnja tega izraza:

1+3+2 = 6

In to je absolutna stopnja polinoma, saj noben drug od izrazov nima večje stopnje.

Postopek za delo s polinomi

Pri delu s polinomi je pomembno biti pozoren na stopnjo iste, saj je na prvem mestu in pred izvajanjem kakršne koli operacije je primerno slediti tem korakom, za katere stopnja zagotavlja zelo pomembne informacije:

-Naročite prednostni polinom v manjšem smislu. Na ta način je izraz z najvišjo oceno na levi strani in tisti z najnižjo na desno.

Vam lahko služi: endecagon

-Zmanjšajte podobne izraze, postopek, ki je sestavljen v dodajanju vseh izrazov enake spremenljivke in stopnje, ki so v algebraično v izrazu.

-Po potrebi se polinomi zaključijo in prekašajo izraze, katerih koeficient je 0, v primeru izraza z nekim eksponentom.

Naročite, zmanjšajte in dokončajte polinom

Glede na polinom p (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + x⁷ -12 Zahteva se, da ga naročite zmanjšano, zmanjšajte podobne izraze, če obstajajo, in dokončati izraze, ki jih manjkajo, da so natančni.

Prva stvar, ki jo je treba iskati, je izraz z glavnim eksponentom, ki je stopnja polinoma, kar se izkaže:

x⁷

Zato je p (x) 7. razred. Nato je naročen polinom, začenši s tem izrazom levo:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Podobni izrazi so zdaj zmanjšani, kar sta naslednje: - 2x in 3x na eni strani. In 7 in -12 na drugem. Če želite zmanjšati, se koeficienti dodajo algebraično in spremenljivka ostane nespremenjena (če se spremenljivka ne pojavi poleg koeficienta, si je treba zapomniti, da je x⁰ = 1):

-2x+3x = x

7 -12 = -5

Ti rezultati se nadomestijo v P (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

In končno se pregleda polinom, da ugotovi, ali eksponent manjka in dejansko, izraz, katerega eksponent je 6, manjka, zato je dokončan z ničlemi, kot je ta:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Zdaj je opaziti, da je polinom ostal 8 izrazov, saj je, kot že rečeno, število izrazov enaka stopnja + 1.

Pomen stopnje polinoma v vsoti in odštevanju

S polinomi se lahko izvajajo vsote in odštevanje, v katerih se dodajo ali odštejejo le podobni izrazi, ki so enaka spremenljivka in enaka stopnja. Če ni podobnih izrazov, je vsota ali odštevanje preprosto navedena.

Vam lahko služi: distribucijska lastnina

Ko je vsota ali odštevanje, je slednja vsota nasprotnega, stopnja nastalega polinoma je vedno enaka ali manjša od stopnje polinoma, ki dodaja večjo stopnjo.

Rešene vaje

- Vaja rešena 1

Poiščite naslednjo vsoto in določite njegovo absolutno stopnjo:

do³- 8AX²  + x³ + 5²X - 6ax² - x³ + 3. mesto³ - 5²x - x³ + do³+ 14AX² - x³

Rešitev

Je polinom dveh spremenljivk, zato je primerno zmanjšati podobne izraze:

do³- 8AX²  + x³ + 5²X - 6ax² - x³ + 3. mesto³ - 5²x - x³ + do³+ 14AX² - x³ =

= a³ + 3. mesto³ + do³ - 8AX² - 6AX²+ 14AX² +5²X - 5a²x+ x³- x³- x³- x³ =

= 5a³ - 2x³

Oba izraza sta 3. razred v vsaki spremenljivki. Zato je absolutna stopnja polinoma 3.

- Vaja Rešena 2

Izrazite kot polinom območje naslednje ploščate geometrijske slike (slika 2 levo). Kakšna je nastala stopnja polinoma?

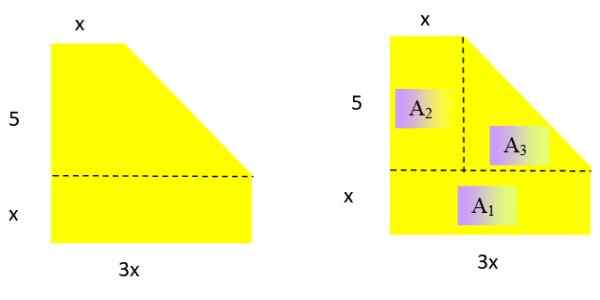Slika 2. Na levi se je številka za leto rešila 2 in na desni, enaka številka se je razpadla na treh območjih, katerih izražanje je znano. Vir: f. Zapata.

Rešitev

Ker je območje, mora biti nastali polinom v razredu 2 v spremenljivki x. Za določitev ustreznega izraza za to območje se številka razdeli na znana območja:

Območje pravokotnika in trikotnika sta: Osnovna višina x in Osnovna x višina /2

Do₁ = x . 3x = 3x²; Do₂ = 5 . x = 5x; Do₃ = 5 . (2x /2) = 5x

Opomba: Osnova trikotnika je 3x - x = 2x in njegova višina je 5.

Zdaj so dodani trije pridobljeni izrazi, s tem imate območje slike, odvisno od x:

3x² + 5x + 5x = 3x² + 10x

Reference

1. Baldor, a. 1974. Elementarna algebra. Venezuelsko kulturno s.Do.
2. Jiménez, r. 2008. Algebra. Dvorana Prentice.
3. Wikilibros. Polinomi. Okrevano od: je. Wikibooks.org.
4. Wikipedija. Razred (polinom). Okrevano od: je.Wikipedija.org.
5. Zill, d. 1984. Algebra in trigonometrija. Mac Graw Hill.