Idealen model plina, vedenje, primeri

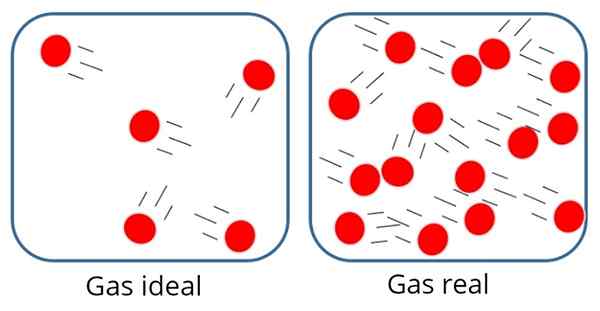
A Idealen plin tudi Popoln plin To je tisto, pri katerem se sila privlačnosti ali molekulskega odbijanja šteje za nepomembno med delci, ki ga sestavljajo, zato je vsa njegova notranja energija kinetična, torej energija, povezana z gibanjem.

V takem plinu so delci običajno precej daleč drug od drugega, čeprav se občasno trčijo drug na drugega in s stenami posode.

V idealnem plinu so delci oddaljeni drug od drugega

Po drugi strani pa v idealnem plinu velikost ali masa delcev ni pomembna, saj naj bi bil volumen, ki ga zasedajo.

To je seveda le pristop, saj v resnici vedno obstaja določena stopnja interakcije med atomi in molekulami. Vemo tudi, da delci zasedajo prostor in imajo maso.

Vendar pa te predpostavke v mnogih primerih, kot so plini z nizko molekulsko maso, delujejo precej dobro, v dobrem območju pritiskov in temperatur.

Vendar se plini z visoko molekulsko maso, zlasti pri visokih tlakih ali nizkih temperaturah, sploh ne obnašajo kot idealni plini in potrebujejo druge modele, ustvarjene z namenom, da jih opišejo z večjo natančnostjo.

[TOC]

Prvi poskusi

Zakoni, ki urejajo pline, so empirični, torej izhajajo iz eksperimentiranja. Najpomembnejši poskusi so bili izvedeni v sedemnajstem, osemnajstem in zgodnjem devetnajstem stoletju.

Najprej so tisti iz Roberta Boylea (1627-1691) in Edme Mariotte (1620-1684), ki sta neodvisno spremenila pritisk v plinu in registrirali njihovo spremembo glasnost, ugotovitev, da so bili obratno sorazmerni: pri večjem pritiskom manjše prostornine.

Robert Boyle

Jacques Charles (1746-1823) je ugotovil ta obseg in temperatura absolutni so bili neposredno sorazmerni, dokler je tlak ostal konstanten.

Lahko vam služi: stacionarne valove: formule, značilnosti, vrste, primeri

Amadeo Avogadro (1776-1856) je odkril, da sta dva enaka količina različnih plinov vsebovala enako količino delcev, dokler sta bila tlak in temperatura enaka. In končno Joseph de Gay Lussac (1778-1850), je dejal, da je s pritrditvijo volumna tlak v plinu neposredno sorazmeren s temperaturo.

Zakoni idealnih plinov

Ta odkritja so izražena s preprostimi formulami, ki kličejo str do pritiska, V do glasnosti, n na število delcev in T Idealna temperatura plina:

Zakon Boyle-Maleotte

Pod pogojem, da je temperatura pritrjena, pride do naslednje:

P⋅v = konstanta

Charles Law

Ko je plin pod stalnim pritiskom:

V / t = konstanta

Gay Lussac Law

Ohranjanje plina v fiksni volumen je res, da:

p / t = konstanta

Avogadro zakon

Enaki količini plina imajo v enakih tlačnih in temperaturnih pogojih enako število delcev. Zato lahko pišemo:

V ∝ n

Kjer je n število delcev in ∝ je simbol sorazmernosti.

Idealen model plina

Idealni plin opisuje plin, ki:

-Ko delci medsebojno delujejo, to storijo zelo kratek čas, z elastičnimi spopadi, v katerih se ohranijo zagon in kinetična energija.

-Njeni sestavni delci so natančni, z drugimi besedami, njegov premer je precej nižji od povprečne razdalje, ki jo potujejo med enim in drugim trkom.

-Medmolekularne sile niso obstoječe.

-Kinetična energija je sorazmerna s temperaturo.

Monoatomski plini - katerih atomi niso povezani med seboj - in nizko molekulsko maso, v standardnih pogojih tlaka in temperature (atmosferski tlak in temperatura 0 ° C), imajo tako vedenje, da je idealni plin zelo dober opis za njim.

Lahko vam služi: Vy Canis Majoris: odkritje, značilnosti, struktura, usposabljanje in evolucija

Idealna enačba stanja plina

Zakoni zgornjih plinov so združeni tako, da tvorijo splošno enačbo, ki ureja idealno vedenje plina:

V ∝ n

V ∝ t

Zato:

V ∝ n⋅t

Poleg tega Boyleovega zakona:

V = konstanta / p

Potem lahko to potrdimo:

V = (konstantna x n⋅t) / p

Konstanta se imenuje plinska konstanta In je označeno s črko r. S to izbiro idealna enačba plina povezuje štiri spremenljivke, ki opisujejo stanje plina, in sicer n, r, p in t, zapuščajo:

P⋅v = n⋅r⋅t

Ta razmeroma preprosta enačba je skladna z zakoni idealnih plinov. Na primer, če je temperatura konstantna, se enačba zmanjša na zakon Boyle-Maleotte.

Konstanta plina

Kot smo že povedali, v standardnih temperaturnih in tlačnih pogojih, torej pri 0 ° C (273.15 K) in 1 tlačno atmosfero je obnašanje številnih plinov blizu idealnega plina. V teh pogojih je prostornina 1 mol plina 22.414 l.

V tem primeru:

R = (p⋅v) / (n⋅t) = (1 atm x 22.414 l) / (1 mol x 273.15 K) = 0.0821 atm ⋅ l /mol ⋅ k

Konstanta plina se lahko izrazi tudi v drugih enotah, na primer v mednarodnem sistemu, če je vredno:

R = 8.314 j⋅ mol^-1⋅ K^-1

Ko se težava odpravi z zakonom o idealnih plinih, je primerno biti pozoren na enote, v katerih je konstanta izražena, saj kot vidimo, obstaja veliko možnosti.

Obnašanje idealnega plina

Kot smo že povedali. Zato je enačba p⋅v = n⋅r⋅t uporabna za iskanje razmerja med štirimi spremenljivkami, ki ga opisujejo: N, P, V in T.

Lahko vam služi: Heisenberg Atomski model

Na ta način si lahko predstavljamo idealen del plina, zaklenjen v posodo in ga tvorimo drobni delci, ki se občasno spopadajo drug z drugim in s stenami posode, vedno elastično.

To je tisto, kar vidimo v naslednji animaciji helijskega dela, plemenitega in monoatomskega plina:

Helij je plemenit plin, v animaciji je del atomov helija prikazan v posodi. Rdeči služijo za boljše razlikovanje gibanja. Vir: Wikimedia Commons.

Primeri idealnih plinov

Idealen plin je hipotetični plin, to je idealizacija, vendar se v praksi v praksi veliko plinov obnaša na zelo blizu.

Plemenite plini

Primer plinov, ki se v standardnih pogojih obnašajo kot ideali, so plemeniti plini, pa tudi lahki plini: vodik, kisik in dušik.

Aerostatski balon

Idealni plinski model pojasnjuje, kako balon vročega zraka. Vir: Wikimedia Commons.

Aerostatični baloni na sliki 1 lahko uporabi Charlesov zakon: plin se segreje, zato se zrak, ki napolni svet, razširi in posledično se dvigne.

Helijev baloni

Helij je skupaj z vodikom najpogostejši element v vesolju, vendar je na Zemlji malo. Ker je plemenit plin inerten, za razliko od vodika, zato se polni baloni helija pogosto uporabljajo kot dekorativni elementi.

Reference

1. Atkins, str. 1999. Fizikalna kemija. Omega izdaje.
2. Chang, R. 2013. Kemija. 11VA. Izdaja. MC Graw Hill Education.
3. Cengel in. 2012. Termodinamika. 7. izdaja. McGraw Hill.
4. Cimbala, c. 2006. Mehanika tekočin, osnov in aplikacij. MC. Graw Hill.
5. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.