Inverzne trigonometrične funkcije, izpeljane, primeri, vaje

The Inverzne trigonometrične funkcije, Kot že ime pove, so to ustrezne obratne funkcije funkcij sinusa, kosinusa, tangenta, cotangenta, sušenja in kombajna.

Inverzne trigonometrične funkcije so označene z isto ime njegove ustrezne neposredne trigonometrične funkcije in predpona LOK. Tako:

1.- Arcsen (x) To je obratna trigonometrična funkcija funkcije greh (x)

2.- Arccos (x) To je obratna trigonometrična funkcija funkcije cos (x)

3.- Arctan (x) To je obratna trigonometrična funkcija funkcije Tan (x)

4.- Arccot ​​(x) To je obratna trigonometrična funkcija funkcije COT (x)

5.- Arcsec (x) To je obratna trigonometrična funkcija funkcije Sec (x)

6.- Arccsc (x) To je obratna trigonometrična funkcija funkcije CSC (x)

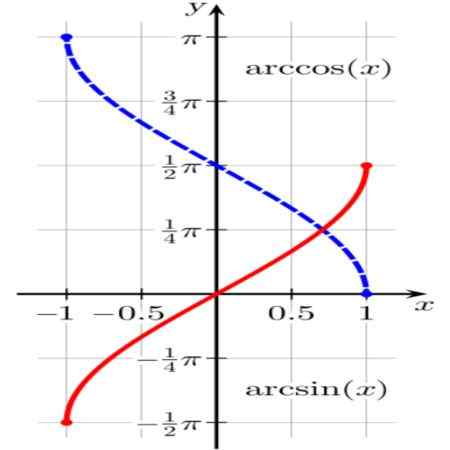
Slika 1. Funkcije Arcsen (x) (v rdeči barvi) in Arccos (x) (v modri barvi). Vir: Wikimedia Commons.

Funkcija θ = arcsen (x) Ima za posledico lok enote θ (ali kot v radianih θ) takšno greh (θ) = x.

Tako je na primer Arcsen (√3/2) = π/3 Ker je, kot je znano, dojka π/3 radians enaka √3/2.

[TOC]

Glavna vrednost inverznih trigonometričnih funkcij

Tako da ima matematična funkcija f (x) inverzno g (x) = f^-1(x) Potrebno je, da je ta funkcija Injektivno, Kar pomeni, da vsaka vrednost in nabor prihoda funkcije f (x) izvira iz ene in samo vrednosti x.

Jasno je, da te zahteve ne izpolni nobena trigonometrična funkcija. Če želite razjasniti točko, opazimo, da lahko vrednost y = 0,5 dobimo iz funkcije sinusa na naslednje načine:

• sin (π/6) = 0,5
• sin (5π/6) = 0,5
• greh (7π/6) = 0,5

In še veliko več, saj je funkcija sinusa periodična z obdobjem 2π.

Lahko vam služi: večkratniki 8: kaj so in razlaga

Za določitev obratno trigonometričnih funkcij je treba omejiti domeno ustreznih neposrednih trigonometričnih funkcij, tako da izpolnjujejo zahtevo po injektivnosti.

Ta omejena domena neposredne funkcije bo glavni razpon ali veja ustrezne obratne funkcije.

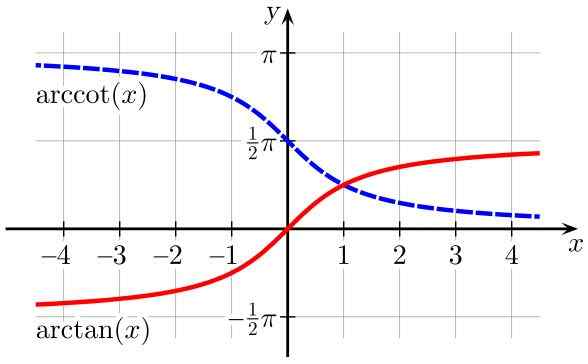Slika 2. Arktanske funkcije (x) (v rdeči barvi) in Arccot ​​(x) (v modrem). Vir: Wikimedia Commons.

Tabela domen in razponov inverznih trigonometričnih funkcij

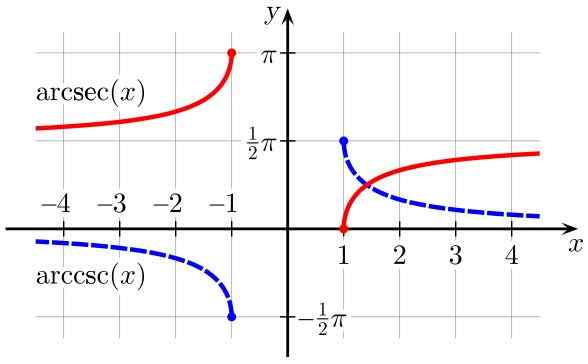Slika 3. ArcSec (x) (v rdeči barvi) in arccsc (x) (v modri barvi) (v modri barvi). Vir: Wikimedia Commons.

Izhaja iz inverznih trigonometričnih funkcij

Za pridobitev derivatov inverzno trigonometričnih funkcij se uporabljajo lastnosti derivatov, zlasti tiste, ki izhajajo iz inverzne funkcije.

Če za F (y) označujemo funkcijo in F^-1(x) do njene obratne funkcije je potem izpeljana iz obratne funkcije povezana z izpeljavo neposredne funkcije z naslednjim razmerjem:

[F^-1(x)] '= 1/ f' [f^-1(x)]

Na primer: Če je x = f (y) = √y neposredna funkcija, bo njegova obratna

y = f^-1(x) = x². Za ta preprost primer uporabimo pravilo obratnega izpeljanega, da vidimo, da je to pravilo izpolnjeno:

[x²] '= 1 / [√Y]' = 1 / (½ in^-½ = 2 in^½ = 2 (x²)^½ = 2x 

No, ta trik lahko ocenimo, da najdemo tiste, pridobljene iz inverznih trigonometričnih funkcij.

Na primer vzamemo θ = arcsen (x) Kot neposredna funkcija bo njegova obratna funkcija greh (θ) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) = ..

… = 1 / √ (1 - x²) .

Na ta način je mogoče dobiti vse tiste, ki izhajajo iz obratnih trigonometričnih funkcij, ki so prikazane spodaj:

Slika 4. Tabela tistih, ki izhajajo iz inverzno trigonometričnih funkcij. Vir: Wikimedia Commons.

Ti derivati ​​veljajo za vse z argumentom, ki pripadajo zapletenim številom, zato veljajo tudi za kateri koli resnični argument X, saj je z = x + 0i.

Vam lahko služi: štirikolesni: elementi, lastnosti, klasifikacija, primeri

Primeri

- Primer 1

Poiščite arctan (1).

Rešitev

Arctan (1) je enotni lok (kot v radianih) ፀ, tako da je porjavelo (ፀ) = 1. Ta kot je ፀ = π/4, ker je tako (π/4) = 1. Potem arctan (1) = π/4.

- Primer 2

Izračunajte lok (cos (π/3)).

Rešitev

Radians kot π/3 je pomemben kot, katerega kosinus je ½, tako da se težava zmanjša na iskanje Arcsena (½).

Torej gre za iskanje kota, katerega sinus daje ½. Ta kot je π/6, saj je Sen (π/6) = Sen (30 °) = ½. Zato Arcsen (cos (π/3)) = π/6. 

Vaje

- Vaja 1

Poiščite rezultat naslednjega izraza:

Sec (Arcan (3)) + CSC (Arccot ​​(4))

Rešitev

Začnemo imenovati α = Arcan (3) in β = lok (4). Torej je izraz, ki ga moramo izračunati, tak:

Sec (α) + csc (β)

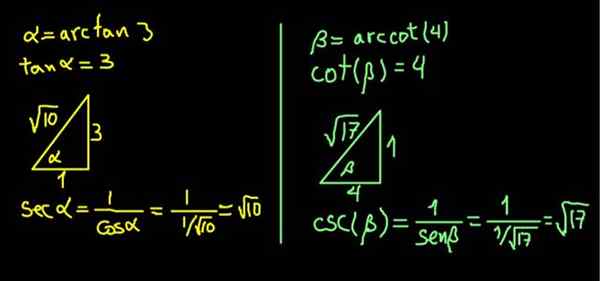
Izraz α = Arcan (3) je enakovreden tako (α) = 3.

Ker je tangenta nasprotna noga na sosednji, je vgrajen pravokotni trikotnik kateta, ki nasprotuje α 3 enote in sosednja kategorija 1 enote, tako da je tako (α) = 3/1 = 3.

V trikotniku pravokotnika hipotenuza določa teorem pitagore. S temi vrednostmi je √10, tako da:

sec (α) = hipotenuza / sosednji cateto = √10 / 1 = √10.

Podobno je β = lok (4) enakovreden, ki navaja, da je COT (β) = 4.

Zgrajen je pravokotni trikotnik kateta, ki meji na β 4 enot in nasprotni kateto 1 enote, tako da je otroška posteljica (β) = 4/1.

Trikotnik je takoj dokončan, če najde svojo hipotenuzo zahvaljujoč teoremu Pythagorasa. V tem primeru se je izkazalo, da ima √17 enot. Nato se izračuna CSC (β) = hipotenuza / nasproti cateto = √17 / 1 = √17.

Lahko vam služi: y = 3sen (4x) funkcijsko obdobje

Če se spomnimo, da je izraz, ki ga moramo izračunati, je: 

sec (Arcan (3)) + CSC (Arcot (4)) = sec (α) + CSC (β) =…

… = √10 + √17 = 3,16 + 4.12 = 7,28.

- Vaja 2

Poiščite rešitve:

Cos (2x) = 1 - sen (x)

Rešitev

Potrebno je, da so vse trigonometrične funkcije izražene v istem argumentu ali kotu. Uporabili bomo identiteto dvojnega kota:

Cos (2x) = 1 - 2 sen²(x)

Potem se izvirni izraz zmanjša na:

1 - 2 Sen²(x) = 1 - greh x

Ko je poenostavljen in faktoriran, je izražen kot:

sin (x) (2 sen (x) - 1) = 0

Kar povzroči dve možni enačbi: sin (x) = 0 z raztopino x = 0 in drugo enačbo sen (x) = ½ z x = π/6 kot rešitev.

Rešitve dvignjene enačbe so: x = 0 ali x = π/6.

- Vaja 3

Poiščite rešitve naslednje trigonometrične enačbe:

cos (x) = greh²(x)

Rešitev

Za rešitev te enačbe je priročno postaviti eno vrsto trigonometrične funkcije, zato bomo uporabili temeljno trigonometrično identiteto, tako da je izvirna enačba napisana na naslednji način:

cos (x) = 1 - cos²(x)

Če poimenujemo y = cos (x), lahko izraz ponovno napišemo kot:

in² + in - 1 = 0

To je enačba druge stopnje v in, katere rešitve so:

y = (-1 ± √5) / 2

Potem so vrednosti x, ki izpolnjujejo prvotno enačbo::

x = arcos ((-1 ± √5) / 2)

Prava rešitev je pozitiven znak x = 0,9046 rad = 51,83 °.

Druga rešitev je zapletena: x = (π - 1,06 i) rad.

Reference

1. Hazewinkel, m. 1994. Enciklopedija matematike. Akademski založniki Kluwer / Springer Science & Business Media. 
2. Mobilni par. Inverzne trigonometrične funkcije. Okreval od: matemovil.com
3. Formule vesolja. Inverzne trigonometrične funkcije. Okrevano od: univerzeformulas.com
4. Weisstein, Eric W. Izumite trigonometrične funkcije. Okreval od: Mathworld.Wolfram.com
5. Wikipedija. Izumite trigonometrične funkcije. Pridobljeno iz: v.Wikipedija.com