Naključna formula in enačbe napak, izračun, primeri, vaje

On naključna napaka fizičnega zneska je sestavljeno iz nepredvidljivih različic ukrepa tega zneska. Te spremembe lahko ustvarijo pojav, ki se meri, z merilnim instrumentom ali samim opazovalcem.

Takšna napaka ni posledica dejstva, da je bilo med poskusom nekaj narobe, ampak da gre za napako, ki je značilna za postopek merjenja ali proučen pojav. To povzroči izmerjeno ukrep včasih nekoliko večji in včasih nekoliko nižji, običajno pa niha okoli osrednje vrednosti.

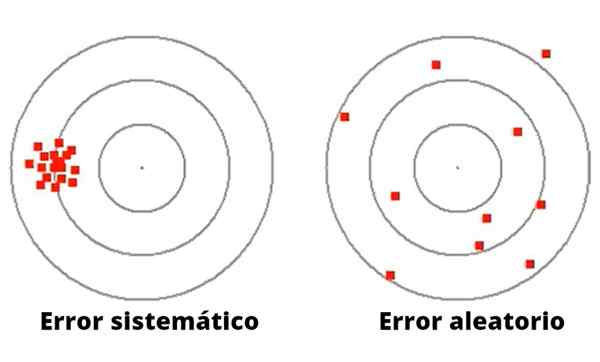
Slika 1- Naključne napake se razlikujejo po velikosti in smeri. Nasprotno, sistematične napake so ponavadi dosledne.

Za razliko od naključne napake lahko sistematično napako povzroči slaba kalibracija ali neprimeren faktor obsega v merilnem instrumentu, vključno z okvaro v eksperimentalni opremi ali neprimernim opazovanjem, ki povzroča odstopanje v enakem smislu.

Slika 1 prikazuje razliko med sistematično in naključno napako v igri za zagon DART do cilja s krogi.

V primeru leve so pikado koncentrirani okoli daleč od središča. Vrč teh pikado, čeprav dobrega cilja, ima sistematičen neuspeh, morda vizualnega izvora ali na poti metanja.

Po drugi strani ima vrč na desni (na sliki 1) veliko disperzijo okoli osrednjega cilja, zato je zelo nenatančen vrč s slabim ciljem, ki nehote naredi naključne napake.

[TOC]

Formule in enačbe v naključni napaki

Ko postopek merjenja pokaže naključno napako, je potrebna.

Seveda je pri vsaki meritvi treba paziti, da so pogoji, v katerih se izvajajo, vedno enaki.

Lahko vam služi: Faraday Law: Formula, enote, poskusi, vadba,

Recimo, da se meritev ponovi n krat. Ker je pri vsaki meritvi naključna napaka, bo nekoliko drugačna vrednost. Recimo nabor n Meritve so:

x₁, x₂, x₃,…, X_n

Torej, kakšno vrednost poročila za ukrep? 

Povprečna vrednost in standardni odklon

The srednja vrednost tudi povprečje Nabora ukrepov, ki jih označujemo in se izračuna na naslednji način:

= (x₁ + x₂ + x₃ +… +X_n) / n

Standardni odklon

Vendar ima ta rezultat mero napake, ki jo daje standardni odklon. Če ga želite določiti, morate najprej vedeti odstopanje in nato odstopanje:

-Odstopanje d_Yo  da ima vsaka izmerjena vrednost Xi Glede povprečne vrednosti je:

d_Yo = x_Yo -

Če bi bilo izračunano povprečje odstopanj, bi ga sistematično pridobili = 0, glede na to: 

= (d₁ + d₂ + d₃ +… +D_n) /n =

= [x₁ - ) + (x₂ - ) +… +(X_n - )]/n

= (x₁+ x₂ +… + X_n) / n - n / n = - = 0

-Povprečnost odstopanj ni koristna za poznavanje disperzije ukrepov. Po drugi strani pa povprečna vrednost kvadrata odstopanj ali variance, označena s σ², ja je.

Izračuna se po naslednji formuli:

σ² = (d₁² + d₂² +.. .+ d_n² ) / (N -1)

V statistiki se ta znesek imenuje odstopanje.  

In na kvadratnem korenu variance je znan kot Standardni odklon σ:

σ = √ [(d₁² + d₂² +.. .+ d_n² ) / (n -1)] 

Standardni odklon σ kaže, da:

1.- 68% izvedenih meritev je vključenih v interval [ - σ, + σ]. 

2.- 95% meritev je v intervalu [ - 2σ, + 2σ].

3.- 99,7% sprejetih ukrepov je v dosegu [ - 3σ, + 3σ].

Kako izračunati naključno napako?

Rezultat merjenja je srednja vrednost od n Meritve, označene in izračunane v skladu z naslednjo formulo:

Lahko vam služi: Areolar Hitrost: kako se izračuna in reši vaje

= (∑x_Yo) / n

Vendar to ni "natančna" vrednost merjenja, saj nanjo vpliva Naključna napaka ε, ki se izračuna tako:

ε = σ / √n

Kje:

σ = √ [(∑ (xi -)² ) / (n -1)]

Končni rezultat merjenja je treba poročati na kateri koli od naslednjih načinov:

1. ± σ / √n = ± ε S 68 -odstotno stopnjo zaupanja.
2. ± 2σ / √n = ± 2ε Z 95 -odstotno stopnjo zaupanja.
3. ± 3σ / √n = ± 3ε Z 99,7 -odstotno stopnjo zaupanja.

Naključna napaka vpliva na zadnjo pomembno številko merjenja, ki običajno sovpada s spoštovanjem merilnega instrumenta. Če pa je naključna napaka zelo velika, lahko na zadnji dve pomembni številki vplivata variacija.

Primeri naključnih napak

Naključne napake se lahko pojavijo v različnih primerih, v katerih je izveden ukrep:

Merjenje dolžine z merilnikom ali pravilom

Ko se dolžina meri s pravilom ali trakovi in ​​odčitki padejo med blagovnimi znamkami lestvice, potem je ocenjena ta vmesna vrednost.

Včasih ima ocena presežek in drugo napako, zato se v postopek merjenja vnese naključna napaka.

Slika 2. Naključne napake se lahko pojavijo, ko se meri dolžina s trakom. Vir: Pikrepo.

Hitrost vetra

Pri merjenju hitrosti vetra se lahko pri branju od enega trenutka v drugega spremenijo zaradi spreminjajoče se narave pojava.

Pri branju glasnosti v diplomiranem valju

Ko se volumen odčita z diplomiranim jeklenko, celo poskuša zmanjšati napako paralage, vsakič, ko se meri, se kot meniskalno opazovanje nekoliko spremeni, zato na ukrepe vpliva naključna napaka.

Lahko vam služi: Prvo ravnotežno stanje: razlaga, primeri, vaje Slika 3.- V laboratoriju za kemijo je mogoče narediti naključne napake pri branju podiplomskega cilindra. Vir: Pexels.

Ko se meri stas otroka

Z merjenjem višine otroka, še posebej, če je nekoliko nemiren, se majhne spremembe drže nekoliko spremenijo.

Pri uporabi lestvice kopalnice

Ko želimo izmeriti svojo težo s kopalnico, majhno spremembo podporne točke, lahko celo sprememba položaja naključno vpliva na meritev.

Vaja rešena

Voziček z igračami se lahko valja po ravni in nagnjeni progi in izmeri s štoparico, ki traja celotno skladbo. 

Meritev poteka 11 -krat, pri čemer skrb za sprostitev vozička z istega mesta, ne da bi pri tem dali nobeni impulz in ohranili popravke naklona.

Nabor dobljenih rezultatov je:

Q

Kakšna je naključna napaka ukrepov?

Slika 4. Vzeti čas igrače Strolle, ki se spušča skozi nagnjeno ravnino. Vir: Fanny Zapata.

Rešitev

Kot je razvidno, pridobljeni rezultati niso edinstveni in se nekoliko razlikujejo.

Prva je izračunati povprečno časovno vrednost spuščanja in pridobiti 3.074545455 sekund.

Ni smiselno vzdrževati toliko decimalk, saj ima vsaka meritev tri pomembne številke in druga decimalka vsakega ukrepa je negotova, saj je na meji cenitve štoparice, zato je rezultat zaokrožen na dve decimali:

= 3,08 s.

S kalkulatorjem v statističnem načinu je standardni odklon σ = 0,03 s In standardna napaka je σ / √11 = 0,01 s. Končni rezultat je izražen na naslednji način:

Čas spuščanja 

3,08 S ± 0,01s (s 68 -odstotno stopnjo zaupanja)

3,08 S ± 0,02S (z 95 -odstotno stopnjo zaupanja)

3,08 S ± 0,03s (z 99,7 -odstotno stopnjo zaupanja)

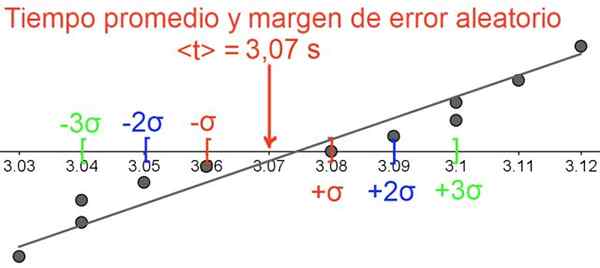Slika 5. Naključna stopnja napake upoštevajte, da so podatki razvrščeni okoli povprečne vrednosti. Vir: f. Zapata.

Reference

1. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
2. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
3. Čelada a. Naključna napaka vs. Sistematična napaka. Okreval od: Thoughtco.com
4. Laredo, e. Srednje napake. Okreval od: USB.pojdi.
5. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.