Transcendentne funkcije Vrste, definicija, lastnosti, primeri

The transcendentne funkcije Elementalni so eksponentni, logaritmični, trigonometrični, obratni trigonometrični funkciji, hiperbolične in inverzne hiperbolične. To pomeni, da so tisti, ki jih ni mogoče izraziti s polinomom, polinomnim ali polinomnim koreninam. 

Neelementne transcendentne funkcije so znane tudi kot posebne funkcije in med njimi lahko poimenujemo funkcijo napak. The Algebrske funkcije (polinomi, polinomni količniki in polinomne korenine) poleg transcendentne funkcije elementi predstavljajo tisto, kar je v matematiki znano kot Osnovne funkcije.

Šteje se tudi za transcendentne funkcije, ki so posledica operacij med transcendentnimi funkcijami ali med transcendentnimi in algebrskimi funkcijami. Te operacije so: vsota in razlika funkcij, izdelka in razmerje funkcij, pa tudi sestava dveh ali več funkcij.

[TOC]

Definicija in lastnosti

Eksponentna funkcija

Je resnična funkcija resnične neodvisne spremenljivke obrazca:

f (x) = a^x = a^x

kje do Je pozitivno resnično število (A> 0) fiksno imenovano bazo. Za označevanje potencialnih operacij se uporabljata Circusflejo ali nadzor.

Vstavimo v primeru A = 2 Potem je funkcija takšna:

f (x) = 2^x = 2^x

Ki bo ocenjena za več vrednosti neodvisne spremenljivke x:

Spodaj je grafika, kjer je predstavljena eksponentna funkcija za več osnovnih vrednosti, vključno z osnovo in (Neper številka in ≃ 2.72). Baza in Tako pomembno je, da na splošno, ko govorite o eksponentni funkciji, razmišljate E^x, to je tudi označeno exp (x).

Slika 1. Eksponentna funkcija a^x, za več vrednosti osnove a. (Lastna izdelava)

Lastnosti eksponentne funkcije

Na sliki 1 je razvidno, da so domena eksponentnih funkcij realna številka (dom f = R) in domet ali pot sta pozitivna resnična (RAN f = R⁺). 

Vam lahko služi: simetrija

Po drugi strani pa vse eksponentne funkcije ne glede na vrednost baze A gredo skozi točko (0, 1) in po točki (1, a). 

Ko je osnova A> 1, Potem funkcija raste in kdaj 0 < a < 1 Funkcija se zmanjšuje. 

Krivulje y = a^x in od y = (1/a)^x  So simetrične glede na osi In. 

Z izjemo primera A = 1, Eksponentna funkcija je injektivna, torej za vsako vrednost slike, ena ustreza in le začetna vrednost.

Logaritmična funkcija

Je resnična dejanska funkcija resnične neodvisne spremenljivke, ki temelji na definiciji logaritma številke. Na osnovi logaritma do številke x, To je številka in na katero je treba vzpostaviti osnovo, da dobimo argument x:

dnevnik_do(x) = y ⇔ a^y = x

To je Funkcija logaritma v bazi do To je obratna funkcija eksponentni funkciji, ki temelji na do.

Na primer:

dnevnik₂1 = 0, saj 2^0 = 1

Drug primer, dnevnik₂4 = 2, ker 2^2 = 4

Koren logaritem 2 je dnevnik₂√2 = ½, ker 2^½ = √2

dnevnik₂ ¼ = -2, glede na to, da je 2^(-2) = ¼ 

Spodaj je graf funkcije logaritma v različnih bazah.

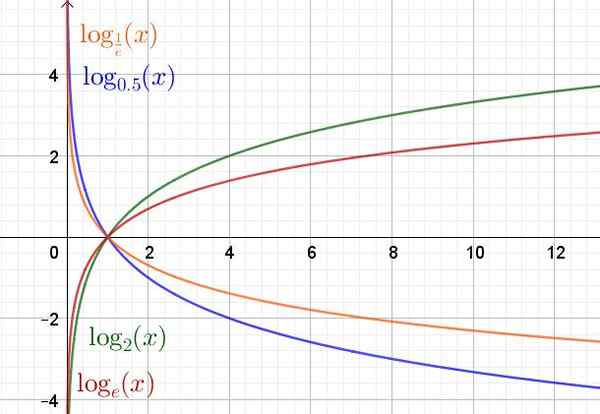Slika 2. Eksponentna funkcija za različne osnovne vrednosti. (Lastna izdelava)

Lastnosti funkcij logaritmo

Domena funkcije logaritma in (x) = dnevnikdo(x)  So pozitivne realne številke R+. Domet ali pot so resnične številke R.

Ne glede na bazo, funkcija logaritma vedno gre skozi točko (1.0) in točka (a, 1) pripada grafu omenjene funkcije.

Lahko vam služi: Teorija čakalnih vrst: Zgodovina, model, kaj je za to in primere za

V primeru, da je baza A večja od enote (a> 1), se funkcija logaritma povečuje. Ampak ja (0 < a < 1) entonces es una función decreciente.

Funkcije Seno, Coseno in Tangent

Sinusna funkcija dodeli resnično število in vsaki vrednosti x, kjer x predstavlja merilo kota v radianih. Za pridobitev vrednosti sen (x) iz kota je kot v krogu enote predstavljen kot, projekcija omenjenega kota pa na navpični osi je dojka, ki ustreza temu kotu.

Spodaj je (na sliki 3) trigonometrični krog in dojke za več kotnih vrednosti x1, x2, x3 in x4.

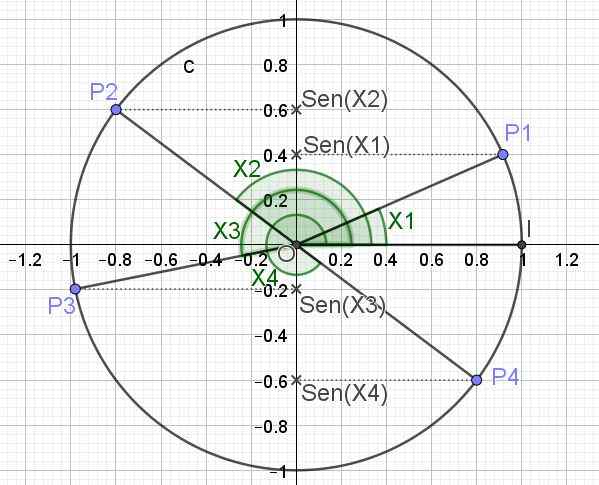Slika 3. Trigonometrični krog in krog več kotov. (Lastna izdelava)

Na ta način je definirana največja vrednost, ki jo ima funkcija Sen (x), je 1, kar se pojavi, ko je x = π/2 + 2π n, ki je n in celo število (0, ± 1, ± 2,). Najmanjša vrednost, ki jo lahko prevzame funkcija sen (x), ko je x = 3π/2 + 2π n. 

Funkcija Coseno y = cos (x) je opredeljena na podoben način, vendar se projekcija kotnih položajev P1, P2 itd. Izvede na vodoravni osi trigonometričnega kroga.

Po drugi strani je funkcija y = tan (x) razmerje med sinusovo funkcijo in kosinusno funkcijo.

Nato je prikazan graf transcendentnih funkcij Sen (x), cos (x) in tan (x)

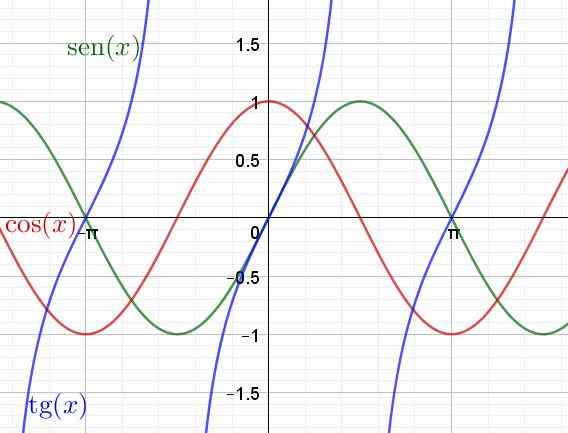Slika 4. Graf transcendentnih funkcij, dojk, kosinusa in tangenta. (Lastna izdelava)

Izpeljan in integral

Izhaja iz eksponentne funkcije

Derivat in eksponentne funkcije y = a^x To je funkcija a^x ga pomnožil Neperijski logaritem baze a:

Vam lahko služi: teorija nastavitve: značilnosti, elementi, primeri, vaje

in '= (a^x)' = a^x ln a

V posebnem primeru baze in, Derivat eksponentne funkcije je sama eksponentna funkcija.

Integral eksponentne funkcije

Nedoločen integral a^x To je funkcija, razdeljena med neperijskim logaritmom baze. 

V posebnem primeru osnove E je integral eksponentne funkcije eksponentna funkcija.

Derivatna in integralna tabela transcendentnih funkcij

Spodaj je povzetek tabele glavnih transcendentnih funkcij, njegovih derivatov in nedoločenih (antiderivativi):

Nedefinita in integralna tabela za nekatere transcendentne funkcije. (Lastna izdelava)

Primeri

Primer 1

Poiščite nastalo funkcijo sestave funkcije f (x) = x^3 s funkcijo g (x) = cos (x):

(f ali g) (x) = f (g (x)) = cos³(x)

Njegov izpeljan in nedoločen integral je:

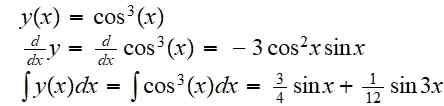
Primer 2

Poiščite sestavo funkcije G s funkcijo F, ki sta G in F funkcije, opredeljene v prejšnjem primeru:

(g ali f) (x) = g (f (x)) = cos (x³)

Treba je opozoriti, da sestava funkcij ni komutativna operacija.

Derivat in nedoločen integral za to funkcijo sta:

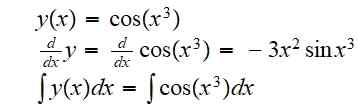
Integral je bil prepuščen, ker rezultata ni mogoče napisati kot kombinacijo osnovnih funkcij na natančno.

Reference

1. Izračun ene same spremenljivke. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. november. 2008
2. Teorem implicitne funkcije: Zgodovina, teorija in aplikacije. Steven G. Krantz, Harold R. Parki. Springer Science & Business Media, 9. november. 2012
3. Multivariabilna analiza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. december. 2010
4. Sistemska dinamika: modeliranje, simulacija in nadzor mehatronskih sistemov. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
5. Calculus: matematika in modeliranje. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick VITRAY. Addison Wesley Longman, 1. januar. 1999
6. Wikipedija. Transcendentna funkcija. Okrevano od: je.Wikipedija.com