Matematične funkcije

Matematična funkcija je razmerje med dvema velikosti, ko je prva odvisna od drugega. Shuttersock

Kaj so matematične funkcije?

The matematične funkcije So izraz v matematičnem jeziku razmerja med dvema spremenljivkama, vrednost prve spremenljivke pa je odvisna od drugega. Običajno so te spremenljivke simbolizirane s črkami x in y.  Spremenljivka X se imenuje domena ali neodvisna spremenljivka; in do y, kodominija ali odvisne spremenljivke.

Poglejmo primer. Imamo dve spremenljivki ali velikosti: dolar in centi. Vemo, da je 100 centov enakovredno dolarju. Zato so centi (x) domena in dolar (y) ustreza kodominiju. To razmerje je mogoče izraziti z naslednjo funkcijo (F):

F (x) = y / 100

Če imam v svoji piggy banki 143 centov in želim vedeti, koliko dolarjev sem prihranil, uporabim samo funkcijo:

F (x) = 143 /100

Zato imam 1,43 dolarja.

Prav tako lahko izrazimo obratno razmerje, to je, da je dolar enakovreden 100 centov. Posledično so vložene kategorije spremenljivk: dolar (x) postane domena, medtem ko je cent kodominium. Izrazimo ga na ta način:

F (x) = x x 100

Če imam v svoji piggy banki 1,43 dolarja, vendar želim vedeti, koliko centov je ta številka enakovredna, je dovolj, da uporabim to drugo funkcijo.

F (x): 1,43 x 100

Rezultat se vrne v mojih 143 originalnih centov.

Spremenljivke matematičnih funkcij

Spremenljivka je preprosto simbol (x, y, z), ki predstavlja različne elemente.

V prejšnjem primeru sta spremenljivka x in y simbolizirala dolar in peni dolarja. Toda enake simbole (x in y) lahko uporabimo za predstavljanje neskončnosti elementov, kot sta: starost osebe in njihova teža; Število letov do določenega cilja in obdobje (na teden, na mesec na leto) itd.

Vam lahko služi: sintetična delitev

Spremenljivke je mogoče razvrstiti v številne vrste, vendar so najpomembnejše za matematične funkcije naslednje:

• Odvisna spremenljivka: tiste, katerih vrednost je odvisna od vrednosti, dodeljene drugim spremenljivkam znotraj funkcije.
• Neodvisna spremenljivka: Spremembe te vrste spremenljivke vplivajo na vrednosti preostalih spremenljivk funkcije.
• Kvantitativna spremenljivka: Izraženo je z določenimi številčnimi zneski. So lahko cele ali decimalne številke.

Značilnosti matematičnih funkcij

1- Razmerje med spremenljivkami je izraženo v enakovrednosti.

2- Za vsako vrednost spremenljivke x obstaja a in le enakovreden spremenljivki in. In obratno: Za določeno vrednost y obstaja A in le rezultat spremenljivke x.

3- Na kartezijanski ravnini jih je mogoče grafično predstaviti, kar omogoča napovedovanje obnašanja ene od spremenljivk iz drugega.

4- Sodobna definicija matematične funkcije je posledica nemškega matematika Petra Dirichleta (1805-1859), ki ga je objavil leta 1837.

Vrste matematičnih funkcij

Matematične funkcije je mogoče razvrstiti po različnih meril, kot je razmerje med spremenljivkami x in y o matematično vedenje funkcije.

Med glavnimi vrstami so naslednje:

Algebrske funkcije

Za njih je značilno vzpostavitev razmerja med komponentami, ki se izražajo bodisi z monomialnim ali polinomom. To razmerje je mogoče določiti s preprostimi matematičnimi operacijami, kot so odštevanje, množenje, delitev, vsota, potenciranje ali oddajanje.

Linearne funkcije

Ko so predstavljeni na kartezijanski ravnini, se pojavijo z obliko ravne črte, ki v določeni točki razreže koordinatno osi. Od tod tudi ime, čeprav so znane tudi kot prve -stopinjske funkcije.

Lahko vam služi: Skupni dejavnik: značilnosti, primeri, vaje

Funkcije na koščke

V tej vrsti vrednost kodominija in spremeni obnašanje funkcije. Zato obstajata dva intervala z različnim vedenjem glede na vrednost domene.

Transcendentne funkcije

So zelo zapletene funkcije. Skupne algebrske operacije niso dovolj (odštevanje, množenje, delitev, vsota, potencial ali sevanje) za določitev razmerja med spremenljivkami, zato je treba uporabiti druga matematična orodja, kot so derivati, integrali ali logaritmi.

Trigonometrične funkcije

Ta vrsta funkcij prikazuje številčni odnos, ki obstaja med različnimi elementi trikotnika in drugimi geometrijskimi figurami, zlasti med njegovimi koti. Formule za dojke, kosinusa, tangenta, secanta in harmonte so primeri te vrste funkcij.

Injektivne funkcije

Za funkcije te vrste je značilna posebnost razmerja med domeno in kodominijem. Za vsako od vrednosti slednjega ustreza samo ena vrednost domene. Prav tako se lahko zgodi, da vrednost domene nima ustrezne vrednosti v kodominiju.

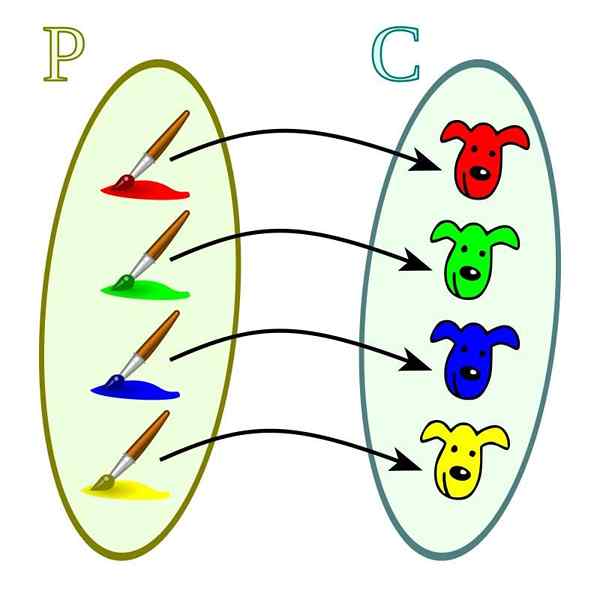Injektivna funkcija. Vir: Wikimedia Commons

Obitne funkcije

V tem primeru je vsaka magnituda kodominija povezana z vsaj eno od vrednosti domene. Razlikujejo se od injektivnih funkcij, v katerih so vrednosti kodominija lahko povezane z več kot ena od vrednosti domene.

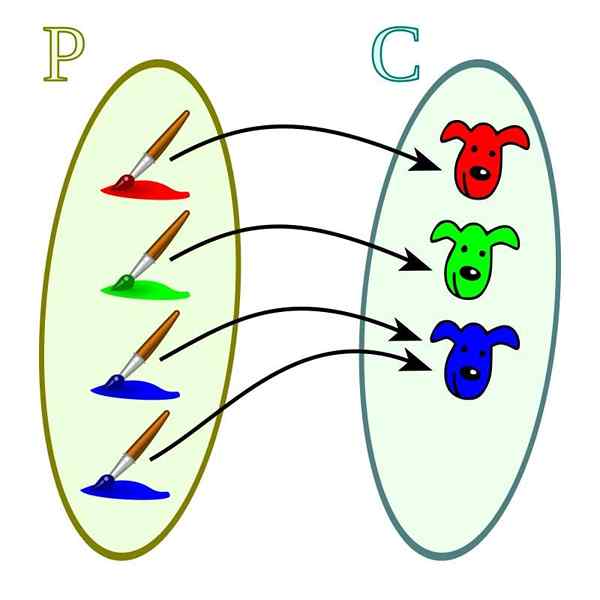Prevelika funkcija. Vir: Wikimedia Commons

Bijektivne funkcije

Ta vrsta funkcij predstavlja tako injektivne kot prekomerne lastnosti.

Za kaj so matematične funkcije?

Funkcije se pogosto uporabljajo v vseh znanostih, ki imajo matematiko kot pomožna znanost. To je primer fizike, inženiringa, medicine, financ, statističnih podatkov, med drugimi.

Vam lahko služi: frekvenčna porazdelitev: kako narediti tabelo, na primer vadbo

V vsakdanjem življenju

Vendar smo lahko koristni tudi za reševanje enostavnejših težav.

Predstavljajte si, da vam je dedek dal 10 kovancev, ki jih boste porabili za čokolado. V kiosku ste desetim kovancem dali odvisnim in mu rekli, naj vam da vse čokolade, ki jih je mogoče kupiti s to količino valut. Dali so vam 5 čokolad. Kakšna je cena vsakega?

Predlagamo težavo: če je 5 čokolad enakovredno 10 kovancev, potem koliko kovancev je enakovredno eni sami čokoladi?

Naša neodvisna spremenljivka (x) je količina čokolade (5), medtem ko odvisna spremenljivka (y) ustreza številu valut, torej 10.

Funkcijo izražamo na naslednji način:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

In že imamo odgovor: vsaka čokolada stane 2 kovanca.

Reference

1. (s/f). Osnovne funkcije. Spletno mesto matematičnih funkcij. Vzeti iz odpadov.Wolfram.com.
2. (s/f). Kaj je funkcija? Vzeti iz matematike.com.