Realna realna spremenljiva funkcija in njegov grafični prikaz

A Prava resnična spremenljiva funkcija Vzemite številko, ki pripada naboru resničnih številk in jo povezuje z drugo vrednostjo, tudi resnično, z edinstvenim pravilom o dopisovanju. To pomeni, da resnično število s tem pravilom pridobi edinstveno sliko.

Numerične spremenljivke odhoda so običajno označene s črka x, medtem ko je njihova slika črka in. Po drugi strani pa se imenuje tudi dopisovno pravilo, ki jih povezuje.  V kompaktnem zapisu je napisano:

F: x → y = f (x)

Slika 1. Graf prave polinomne funkcije

Do spremenljivke  x se imenuje neodvisna spremenljivka, medtem ko in Je odvisna spremenljivka. Funkcija se lahko izrazi na več načinov, na primer z matematično izjavo, kot je ta:

• f (x) = 2x −3
• H (x) = −3x²
• 

Druga oblika izražanja je skozi graf, ki je zelo koristen, ker vam omogoča, da cenite vedenje funkcije enega samega pogleda. Gradnja grafa je zelo preprosta z uporabo kartezijanskega koordinatnega sistema, v katerem so vrstniki [x, f (x)] predstavljeni kot točke v ravnini. Nato se pridružijo mehki in neprekinjeni črti, vidite, kako je funkcija.

Primeri

Za izdelavo grafa se lahko zatečete k tabeli vrednosti, v kateri so postavljene točke na graf. Za spremenljive vrednosti X so izbrane, ki pripadajo domeni funkcije, to je tiste, ki ob zamenjavi v formuli kažejo resnične številke.

Ko so izbrane vrednosti x, je določena njegova slika y = f (x) in na ta način dobimo pare [x, f (x)], ki bodo grafični.

Vam lahko služi: homografska funkcija: kako graditi, rešiti vaje

V tabeli je nekaj točk, ki so pomembne in jih je treba vključiti: tiste, v katerih se graf razreže na koordinatne osi, da če obstajajo, ker jih ne presegajo vse funkcije.

Če jih želite izračunati, nadaljujte na naslednji način:

-Križišče z osi in: x = 0 je narejen v formuli funkcije in izračuna se ustrezna vrednost.

-Križišče z osi x: Y = 0 je narejeno in enačba f (x) = 0 je razrešena.

Nato je narisan kartezijanski koordinatni sistem in vsaka od točk je prikazana, ki se nato povežejo z mehko in neprekinjeno črto, če je mogoče.

Primer 1

Sestavite tabelo vrednosti in graf naslednje funkcije:

f (x) = x² −4

Preden začnete, morate najti domeno funkcije, ki je niz resničnih vrednosti, za katere funkcija obstaja. Ker gre za kvadratno funkcijo, ima vsaka vrednost X, ki spada v resnične številke, resnično sliko, v skladu s F (x).

Nato lahko tabelo sestavite tako, da izberete katero koli vrednost x, najpreprostejša stvar pa je, da začnete s presečišči grafa z osi, če obstajajo. Ko jih najdemo, se za dokončanje mize iščejo druge točke.

Za x = 0

f (0) = -4

Zato je prva točka v tabeli (0, -4). To je presečišče grafa z osi in.

Za y = 0

Potem je Y = 0 narejen in enačba, ki je rezultat, je rešena:

x² −4 = 0

x² = 4

Rešitve te enačbe so: x₁= 2 in x₂= -2. Zato obstajata dva križišča z osi x, ki sta točka: (−2.0) in (2.0).

Vam lahko služi: popolne številke: kako jih prepoznati in primere

Zdaj lahko najdete več točk, ki jih lahko dodate v tabelo vrednosti:

Za x = 1

f (1) = (1)² - 4 = −3

Za x = - 1

f (−1) = (−1)² - 4 = −3

Za x =  3

f (3) = (3)² - 4 = 5

Za x =  -3

f (−3) = (−3)² - 4 = 5

Tabela vrednosti

Naslednja tabela prikazuje pridobljene točke, ki bodo služile za izdelavo grafa F (x):

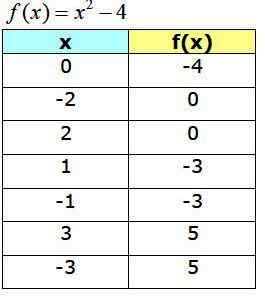Graf funkcije F (x) = x² −4

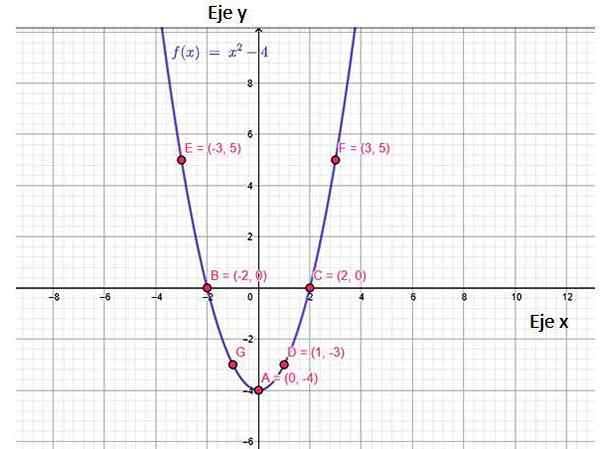Slika 2. Funkcija f (x) funkcijski graf, ki prikazuje nekaj točk, ki mu pripadajo, vključno s križišči z osi. Vir: f. Zapata, prek Geogebre.

Graf te funkcije je prispodoba, ki se odpre in ima na najmanjši točki, imenovana Vertex, koordinat (0, −4). Zanimivo je, da se vrednosti f (x) začnejo pri y = -4 do ∞. To je obseg funkcije.

Iz grafa je mogoče sklepati, da je funkcija neprekinjena, v intervalu (−∞, 0) se zmanjšuje in od tam narašča.

Primer 2

Če ima grafikon funkcije, je mogoče poznati njegovo domeno, njegovo območje, križišča, ki jih ima z osi, in vizualizira njegovo splošno vedenje (rast in zmanjšanje).

Spodaj je graf polinomne funkcije:

f (x) = - x⁴+4x²+1

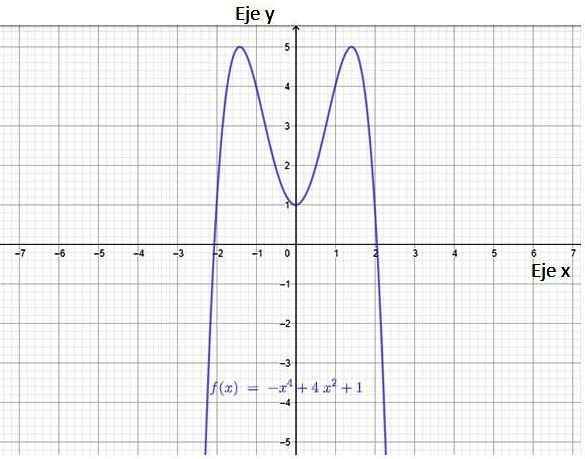Slika 3. Graf polinomne funkcije. Vir: f. Zapata skozi Geogebro.

Iz slike izhaja, da ima funkcija dva križišča z osi x, točkami (-2,0) in (2.0). Ima tudi križišče z osi y, točko (0,1).

Domena polinomne funkcije je celoten niz realnih števil, opozorjeno pa je, da je funkcija neprekinjena in ima simetrijo okoli navpične osi. Dejansko je mogoče preveriti, ali je ta funkcija Simetrija za. Funkcija je tudi, če se sreča:

Vam lahko služi: zeleni teorem, demonstracije, aplikacije in vaje

f (x) = f (-x)

Bralec lahko preveri, da z zamenjavo -x v funkciji ni spremenjen.

Obstajata dve zanimivi točki, ki sta na višini y = 5, najvišje vrednosti funkcije. Obseg te funkcije, to je niz vrednosti, ki jih spremenljivka vzame in se razširi od -∞ do y = 5 natančno.

Če želite vedeti vrednosti x, katerih slika je y = 5, se ta vrednost nadomesti v funkciji:

5 = - x⁴+4x²+1

In ta enačba je pridobljena:

- x⁴ + 4x² - 4 = 0

Katerih rešitve so −plo in + √2. No, funkcija je:

-Raste Od x -∞ do x = −√2

-Zmanjšanje Od x = −√2 do x = 0

-Raste Od x = 0 do x = + √2

-Zmanjšanje Od x = + √2 naprej.

Vaja rešena

Zgradite graf naslednje funkcije:

f (x) = √ (x-5)

Rešitev

Najprej morate določiti domeno funkcije, da veste, katere vrednosti X lahko izberete za izdelavo tabele. V primeru predlagane funkcije mora biti količina znotraj korenine vedno pozitivna ali enaka 0, torej:

x - 5 ≥ 0

x ≥ 5

Zato lahko za tabelo izberemo le vrednosti, večje ali enake. Kar zadeva križišča s koordinatnimi osi, je edina možnost narediti y = 0, nato pa x = 5.

Za to funkcijo je neuporabno narediti x = 0, saj ta vrednost ne pripada domeni.

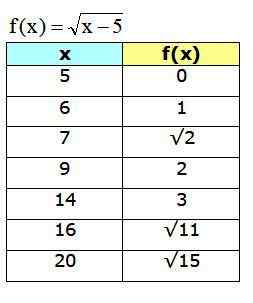
Pridobljeni graf je:

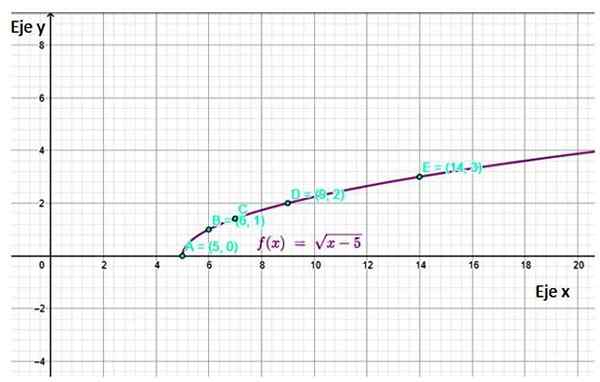Slika 4. Graf funkcije F (x), ki prikazuje nekatere točke, izračunane v tabeli. Vir: f. Zapata skozi Geogebro.

Reference

1. Cona e-math. Vrste funkcij. Okreval od: emathzone.com.
2. Hoffman, J.G. Izbira vprašanj matematike. Ed. Sphinx.
3. Matematika je zabavna. Commons deluje referenca. Okreval od: MathisFun.com.
4. Requena, b. Formule vesolja. Vrste funkcij. Okrevano od: univerzeformulas.com.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.