Injektivna funkcija, iz česa je sestavljena, kaj je za in primere

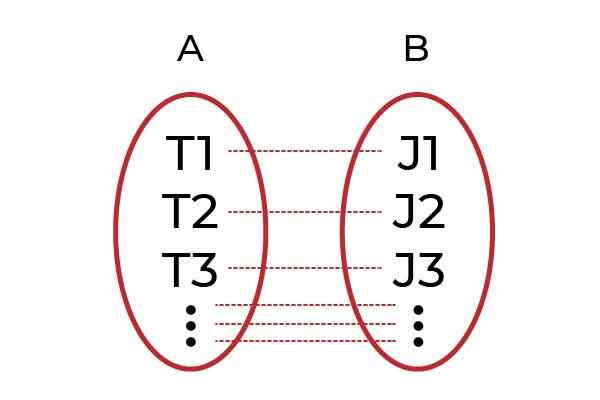
A Injektivna funkcija To je vsak odnos domenskih elementov z enim elementom kodominija. Znana tudi kot funkcija ena za drugim ( enajst ) so del klasifikacije funkcij glede načina povezave njihovih elementov.

Element kodominija je lahko le slika enega samega elementa domene, na ta način vrednosti odvisne spremenljivke ni mogoče ponoviti.

Vir: Avtor.

Jasen primer bi bil, da se združi moške z delom v skupini A in v skupini B vsem šefom. Funkcija F To bo tisti, ki vsak delavec povezuje s svojim šefom. Če je vsak delavec povezan z drugim šefom F, tako F  To bo eno Injektivna funkcija.

Razmisliti Injektivno Naslednje je treba izpolniti funkcijo:

∀ x₁  ≠ x₂   ⇒ F (x₁ ) ≠ f (x₂ )

To je algebrski način Za vse x₁ drugačen od x₂ Imate f (x₁ ) Drugačen od f (x₂ ).

[TOC]

Za kaj so injektivne funkcije?

Injekcija je lastnost neprekinjenih funkcij, saj zagotavljajo dodelitev slik za vsak element domene, kar je bistven vidik v kontinuiteti funkcije.

Pri risanju črte vzporedno z osi X Na grafu injektivne funkcije se je treba dotakniti samo grafa na eni točki, ne glede na višino ali velikost In Črta je narisana. To je grafični način za dokazovanje injekcije funkcije.

Drug način za preizkus, če je funkcija Injektivno, je čiščenje neodvisne spremenljivke X V smislu odvisne spremenljivke In. Potem je treba preveriti, če domena tega novega izraza vsebuje realne številke, hkrati kot za vsako vrednost In Obstaja ena sama vrednost X.

Nalodne funkcije ali odnosi med drugimi oblikami ubogajo zapis F: d_F→C_F

To se glasi F, ki gre od D_F do c_F

Kjer je funkcija F Povežite sklope Domena in Kodominij. Znan tudi kot začetni in nabor prihodov.

Vam lahko služi: naključno vzorčenje: metodologija, prednosti, slabosti, primeri

Dominion D_F  Vsebuje dovoljene vrednosti za neodvisno spremenljivko. Kodominij C_F  Tvori vse razpoložljive vrednosti do odvisne spremenljivke. Elementi C_F navezujoč se D_F  Vedo, kako Razpon funkcij (r_F ).

Kondicioniranje funkcij

Včasih lahko funkcija, ki ni injektivna, podvrže določeni kondiciji. Ti novi pogoji lahko to spremenijo v Injektivna funkcija. Vse vrste sprememb domene in kodominija funkcije so veljavne, kjer je cilj izpolniti lastnosti injektivnosti v ustreznem razmerju.

Primeri injektivnih funkcij z rešenimi vajami

Primer 1

Biti funkcija F: r → R definirana s črto F (x) = 2x - 3

O: [Vse resnične številke]

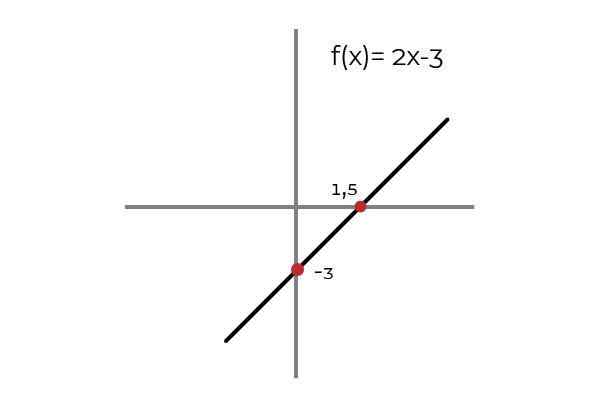Vir: Avtor.

Opazimo, da za katero koli vrednost domene obstaja slika v kodominiju. Ta slika je edinstvena, zaradi česar je F injektivna funkcija. To velja za vse linearne funkcije (funkcije, katerih večja stopnja spremenljivke je ena).

Vir: Avtor.

Primer 2

Biti funkcija F: r → R definirano s F (x) = x² +1

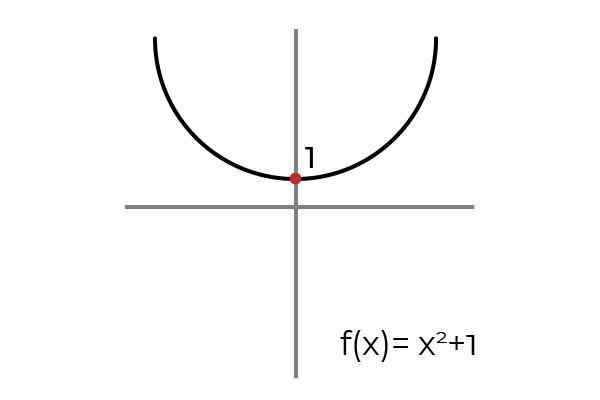Vir: Avtor

Pri risanju vodoravne črte opazimo, da graf najdemo večkrat. Zaradi tega je funkcija F ni in injektivno, medtem ko je definiran  R → R

Domena funkcije je pogojena:

                                               F: r⁺ Ali 0 → R

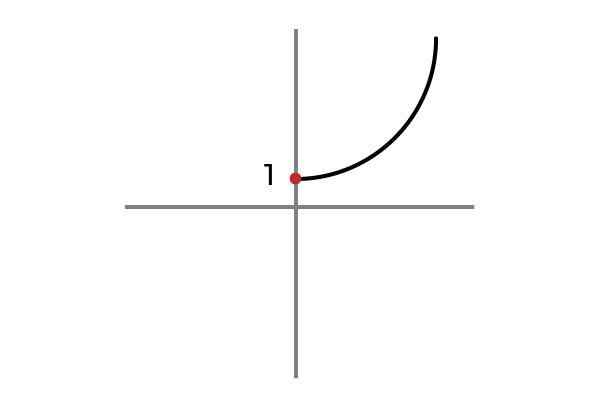Vir: Avtor

Zdaj neodvisna spremenljivka ne sprejme negativnih vrednosti, na ta način se izogne ​​ponovitvi rezultatov in funkcije F: r⁺ Ali 0 → R definirano s F (x) = x² + 1 je injektivno.

Druga homologna rešitev bi bila omejitev domene na levo, to je, da funkcijo omejijo na samo negativne in ničelne vrednosti.

Domena funkcije je pogojena

                                               F: r^- Ali 0 → R

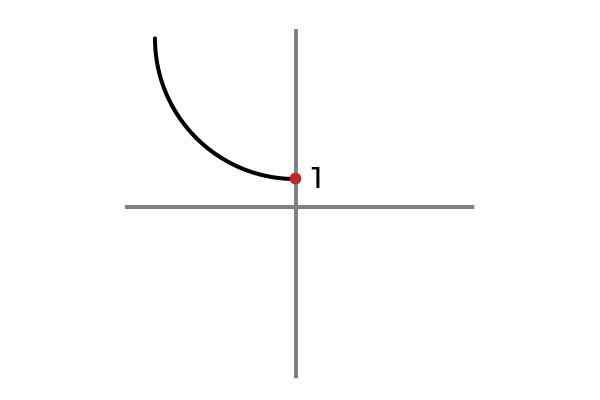Vir: Avtor

Zdaj neodvisna spremenljivka ne sprejme negativnih vrednosti, na ta način se izogne ​​ponovitvi rezultatov in funkcije F: r^- Ali 0 → R definirano s F (x) = x² + 1 je injektivno.

Trigonometrične funkcije imajo vedenje, podobno valovom, kjer je zelo pogosto najti ponovitve vrednosti v odvisni spremenljivki. S posebno kondicijo lahko na podlagi predhodnega poznavanja teh funkcij omejimo domeno, da izpolnjuje pogoje injekcije.

Vam lahko služi: Coplanares Točke: enačba, primer in rešene vaje

Primer 3

Biti funkcija F: [ -π/2, π/2 ] → R definirano s F (x) = cos (x)

V intervalu [ -π/2 → π/2 ] Kosinusna funkcija spreminja svoje rezultate med ničlo in eno.

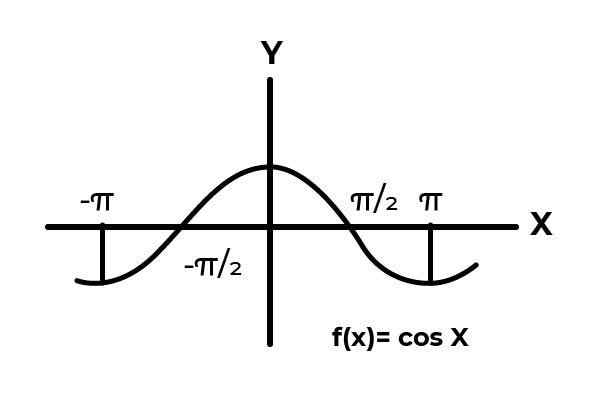Vir: Avtor.

Kot je razvidno iz grafike. Začnite iz nič x = -π/2 nato doseže največ nič. Je po x = 0 da se vrednosti začnejo ponavljati, dokler se ne vrnejo na nič x = π/2. Na ta način je znano, da F (x) = cos (x) ni injektiven Za interval [ -π/2, π/2 ] .

Pri preučevanju grafike funkcije F (x) = cos (x) Intervali opazimo, kjer se vedenje krivulje prilagaja kriterijem injekcije. Kot je interval

[0 , π ]

Kjer se funkcija razlikuje od 1 do -1, ne da bi v odvisni spremenljivki ponavljali kakršno koli vrednost.

Na ta način funkcija funkcija F: [0 , π ] → R definirano s F (x) = cos (x). Je injektivna

Obstajajo nelinearne funkcije, kjer so predstavljeni podobni primeri. Za racionalne izraze, v katerih je imenovalec vsaj ena spremenljivka, obstajajo omejitve, ki preprečujejo injektivnost razmerja.

Primer 4

Biti funkcija F: r → R definirano s F (x) = 10/x

Funkcija je opredeljena za vse realne številke, razen 0 ki predstavlja nedoločnost (ni mogoče razdeliti med ničlo).

Ko se približate ničli na levi strani, odvisna spremenljivka traja zelo velike negativne vrednosti in takoj po ničli vrednosti odvisne spremenljivke prevzamejo velike pozitivne številke.

Ta motnja naredi izraz F: r → R definirano s F (x) = 10/x

Ne bodite vbrizgani.

Kot je razvidno iz prejšnjih primerov, izključitev vrednosti v domeni služi za "popravilo" te nedoločene. Zero je izključena iz domene, pri čemer je nabor in nabor prihodov opredeljenih na naslednji način:

R - 0 → R

Kje R - 0 simbolizira resnično, razen nabora, katerega edini element je nič.

Na ta način izraz F: r - 0 → R definirano s F (x) = 10/x je injektivno.

 Primer 5

Biti funkcija F: [0 , π ] → R definirano s F (x) = greh (x)

V intervalu [0 , π ] Funkcija sinusa spreminja svoje rezultate med ničlo in eno.

Vam lahko služi: naključna spremenljivka: koncept, vrste, primeri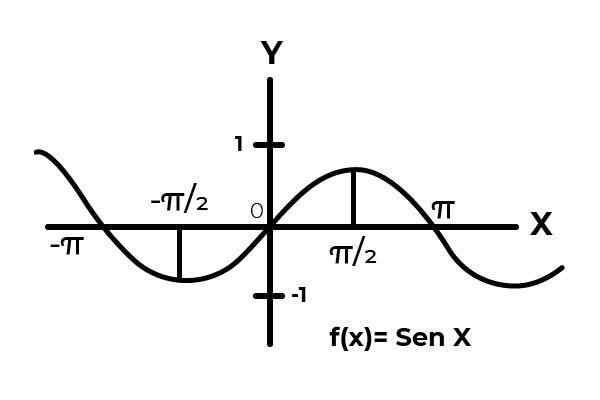Vir: Avtor.

Kot je razvidno iz grafike. Začnite iz nič x = 0 nato doseči največ v x = π/2. Je po x = π/2, da se vrednosti začnejo ponavljati, dokler se ne vrnejo na nič x = π. Na ta način je znano, da F (x) = sin (x) ni injektiven Za interval [0 , π ] .

Pri preučevanju grafike funkcije F (x) = greh (x) Intervali opazimo, kjer se vedenje krivulje prilagaja kriterijem injekcije. Kot je interval  [  π/2,3π/2  ]

Kjer se funkcija razlikuje od 1 do -1, ne da bi v odvisni spremenljivki ponavljali kakršno koli vrednost.

Na ta način je funkcija F: [  π/2,3π/2  ] → R definirano s F (x) = greh (x). Je injektivna

Primer 6

Preverite, ali je funkcija F: [0, ∞) → R definirano s F (x) = 3x² Je injektivna.

Ob tej priložnosti je domena izraza že omejena. Opažamo tudi, da se odvisne spremenljive vrednosti v tem intervalu ne ponavljajo.

Zato je mogoče sklepati, da F: [0, ∞) → R definirano s F (x) = 3x²   Je injektivna

Primer 7

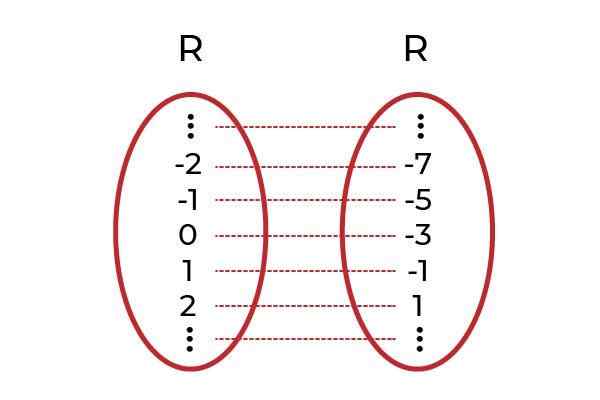
Ugotovite, katera od naslednjih funkcij je

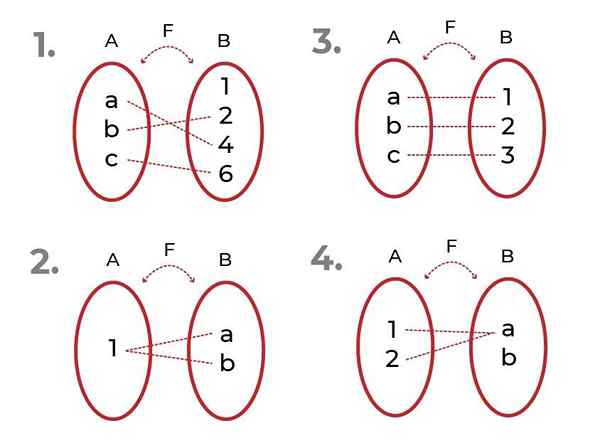Vir: Avtor

1. Je injektivna. Povezani elementi kodominija so edinstveni za vsako vrednost neodvisne spremenljivke.
2. Ni injektivno. Obstajajo elementi Co -ooMinium, povezani z več kot enim elementom začetnega niza.
3. Je injektivna
4. Ni injektivno

Predlagane vaje za razred/hišo

Preverite, ali so naslednje funkcije injektivne:

F: [0, ∞) → R definirano s F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R definirano s F (x) = tan (x)

F: [ -π,π  ] → R definirano s F (x) = cos (x + 1)

F: r → R definirana s črto F (x) = 7x + 2

Reference

1. Uvod v logiko in kritično razmišljanje. Merrilee h. Losos. Univerza v Pittsburghu
2. Težave v matematični analizi. Piotr Bilar, Alfred Witkowski. Univerza v Wroclawu. Palica.
3. Elementi abstraktne analize. Mícheál o'searcoid doktorat. Oddelek za matematiko. University College Dublin, Beldfield, Dublind 4.
4. Uvod v logiko in metodologijo deduktivnih znanosti. Alfred Tarski, New York Oxford. Oxford University Press.
5. Načela matematične analize. Enrique Linés Escardó. Uredništvo Reverté s. Do leta 1991. Barcelona, ​​Španija.