Lastnosti eksponentne funkcije, primeri, vaje

The eksponentna funkcija To je matematična funkcija, ki je zelo pomembna za številne aplikacije, ki jih ima. Opredeljen je na naslednji način:

f (x) = b^x, Z b> 0 in b ≠ 1

Kjer je B resnična konstanta vedno pozitivna in drugačna od 1, ki je znana kot baza. Upoštevajte, da je prava spremenljivka x je v eksponent, Na ta način je f (x) vedno resnično število.

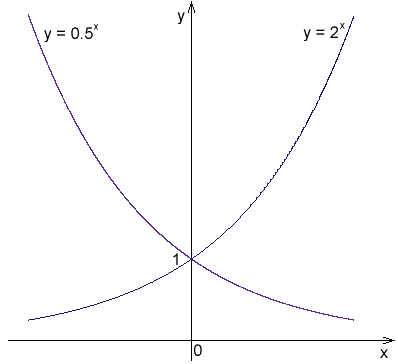Slika 1. Eksponentne funkcije z bazami 2 in 1/2

Primeri eksponentnih funkcij so naslednji:

-f (x) = 2^x

-g (x) = 5⋅E^-3x

-H (x) = 4⋅ (10^2x)

To so funkcije, ki v skladu z znakom eksponenta rastejo - ali se zmanjšujejo - zelo hitro, zato se govori o "eksponentni rasti", ko se nekaj hitro poveča. Zato so primerni za modeliranje rasti živih bitij, kot so bakterije.

Druga zelo zanimiva aplikacija je tista interesa. Več denarja imate na računu, več interesov in lahko izračunajo vsak določen časovni interval, tako majhen, kot želite.

S pomočjo logaritmične funkcije, ki je obratna funkcija eksponenta, je mogoče poznati po tem, kako dolgo se določen kapital poveča na določeno vrednost.

[TOC]

Lastnosti eksponentne funkcije

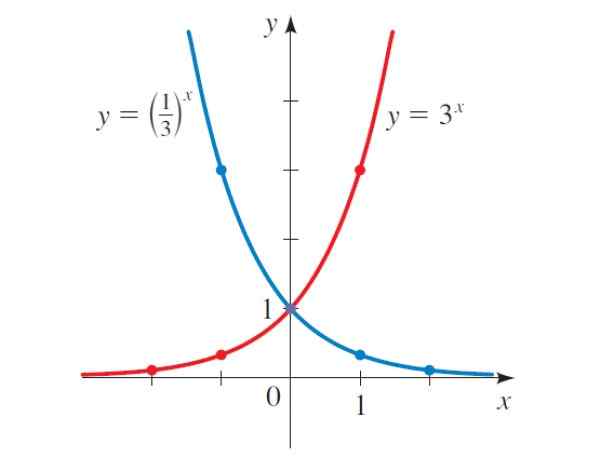
Slika 2. Primeri eksponentnih funkcij. Vir: f. Zapata.

Sledijo splošne lastnosti katere koli eksponentne funkcije:

-Graf katere koli eksponentne funkcije vedno seka navpične osi v točki (0,1), kot je razvidno iz slike 2. To je zato, ker B⁰ = 1 za katero koli vrednost B.

-Eksponentna funkcija se ne seka na osi x, pravzaprav je ta os vodoravna asimptota za funkcijo.

-Od b¹ = B, točka (1, b) vedno pripada grafiki funkcije.

Lahko vam služi: hepagonska prizma

-Domena eksponentne funkcije je niz realnih števil in f (x) = b^x V vsej svoji domeni je neprekinjen.

-Obseg eksponentne funkcije je vsa realna številka večja od 0, kar je opaziti tudi z grafiko.

-Eksponentna funkcija je ena za drugo, torej vsaka vrednost X, ki pripada domeni funkcije, ima edinstveno sliko v naboru prihoda.

-Inverzna eksponentna funkcija je logaritmična funkcija.

Posebne lastnosti eksponentne funkcije

Kot smo že povedali, se lahko eksponentna funkcija povečuje ali zmanjšuje.

Če je graf slike 2 skrbno preučen, je ugotovljeno, da če B> 1, funkcija raste, na primer y = 3^x, Toda v primeru y = (1/3)^x, z b < 1, la función decrece.

Imamo dve vrsti eksponentnih funkcij z naslednjimi določenimi lastnostmi:

Za b> 1

-Funkcija vedno raste.

-Ko se vrednost B poveča, funkcija raste hitreje, na primer y = 10^x raste hitreje kot y = 2^x.

-Ko je spremenljivka večja od 0, funkcija pridobi vrednosti, večje od 1, to je:

Za x> 0: y> 1

-In če x<0, entonces f(x) < 1.

Za b < 1

-Funkcija se vedno zmanjšuje.

-Z zmanjšanjem vrednosti B se funkcija še vedno zmanjšuje. Na primer y = (1/5)^x zmanjšuje hitreje kot y = (1/3)^x.

-Za vrednosti x nižje od 0 funkcija ima vrednosti večje od 1, to je:

Za x 1

-Končno, ko x> 0, potem in < 1.

Primeri eksponentnih funkcij

Eksponentna funkcija je zelo uporabna za modeliranje pojavov v znanosti in gospodarstvu, kot bomo videli spodaj:

Naravna eksponentna funkcija

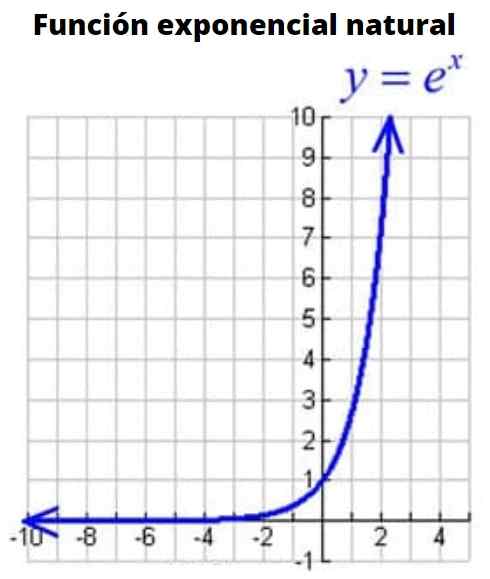Slika 3: Graf naravne eksponentne funkcije

To je funkcija, katere osnova je številka E ali Eulerjeva številka, iracionalna številka, katere vrednost je:

Vam lahko služi: dodatni koti: kaj so, izračun, primeri, vaje

E = 2.718181828…

Ta osnova, tudi če ni okrogla številka, deluje zelo dobro za številne aplikacije. Zato velja za najpomembnejšo osnovo vseh eksponentnih funkcij. Naravna eksponentna funkcija je izražena na matematičen način kot:

f (x) = e^x

Eksponentna funkcija se pogosto pojavlja v verjetnosti in statistiki, saj se lahko z eksponentnimi funkcijami izrazijo različne porazdelitve verjetnosti, kot so običajna porazdelitev, Poisson in druge.

Neprekinjeno sestavljeno zanimanje

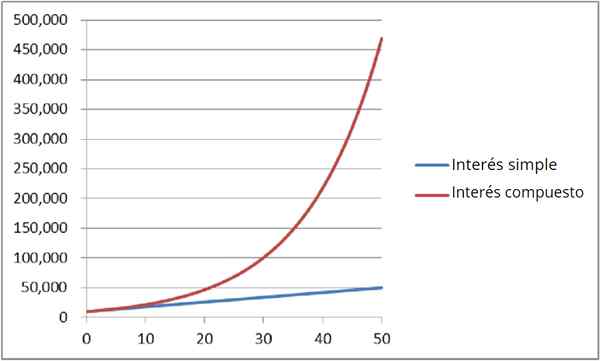Slika 4: Primerjava preprostega in sestavljenega zanimanja

Prav tako se imenuje Neprekinjena kapitalizacija. Vedeti, koliko denarja Do Imate po t Leta se uporablja eksponentni izraz:

A (t) = p ⋅ e^Rt

Kadar je P znesek denarja, ki je bil prvotno položen, je r obrestna mera na leto in končno t je število let.

Rast bakterij

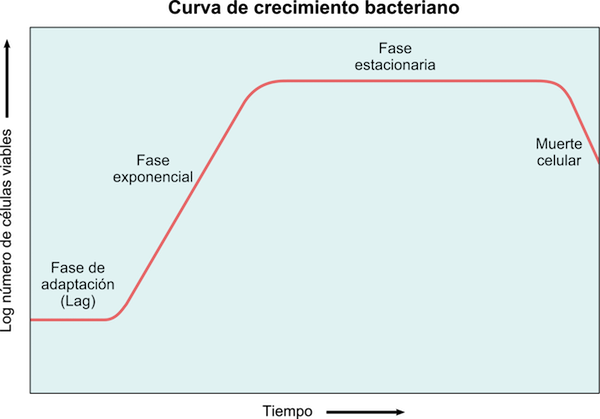Slika 5: Krivulja rasti bakterij, kjer opazimo faze zamud, eksponentnih, stacionarnih in smrti

Bakterije rastejo eksponentno, zato lahko rast modeliramo z:

N (t) = n_tudi ⋅ e ^Kt

Kjer je n (t) obstoječe prebivalstvo po času t (skoraj vedno v urah), n_tudi To je začetna populacija in K je konstanta, ki je odvisna od vrste bakterije in pogojev, pod katerimi so na voljo hranila.

Radioaktivno razpadanje

Določena jedra v naravi so nestabilna, zato se zavrnijo, da se preoblikujejo v bolj stabilne, postopek, ki je lahko zelo kratek ali traja več tisoč let, odvisno od izotopa. Med radioaktivnimi razpadnimi delci se oddajajo in včasih tudi fotoni.

Nekateri radioaktivni izotopi imajo medicinske aplikacije, na primer radioaktivni jod I-131, ki ga zdravniki uporabljajo pri diagnozi in zdravljenju nekaterih stanj ščitnice.

Radioaktivno razpadanje je modelirano z eksponentno funkcijo.

Vam lahko služi: koliko desetin je v enoti?

Rešene vaje

Enačbe, v katerih se neznano pojavlja kot eksponent, se imenujejo eksponentne enačbe. Za odstranjevanje vrednosti neznanih se uporabljajo različne algebrske manipulacije in uporaba funkcije logaritma, ki je obratna funkcija eksponenta.

Poglejmo nekaj rešenih vaj, ki ponazarjajo točko.

- Vaja 1

Rešite naslednje eksponentne enačbe:

do 5^x = 625

b) 5^x = 2^X-1

Rešitev

Številka 625 je v veljavi večkratna od 5, ko ga razgradimo, ugotovimo, da:

625 = 5⁴

Zato lahko pišemo:

5^x = 5⁴

Ker so baze enake levi in ​​desni, se lahko ujemamo z eksponenti in pridobimo:

x = 4

Rešitev b

Za to vajo se ne moremo zateči k prej uporabljeni tehniki, saj baze niso enake. Toda na ta način lahko na obeh straneh enakosti uporabimo logaritem:

5^x = 2^X-1

Dnevnik (5^x) = dnevnik (2^X-1)

Zdaj je uporabljena naslednja lastnost logaritmov:

Dnevnik mⁿ = n⋅log m

In ostane:

x⋅log 5 = (x-1) ⋅Log 2

x⋅ (log 5 - log 2) = -log 2

x = - dnevnik 2 ÷ (dnevnik 5 - dnevnik 2)

- Vaja 2

Navedite, v katero funkcijo vsaka od spodaj prikazanih grafov ustreza:

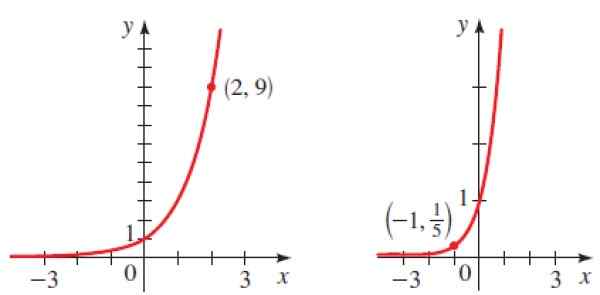Slika 6. Grafika Parasta Eksponentne funkcije rešene vaje 2. Vir: Stewart. J. Prekalenkulacija.

Rešitev

Ker gre za rastoči graf, je B večji od 1 in vemo, da točka (2.9) pripada grafu, torej:

y = b^x → 9 = b²

Vemo, da 3² = 9, torej b = 3 in funkcija je y = 3^x

Rešitev b

Spet nadomestimo dano točko (-1, 1/5) pri y = b^x dobiti:

1/5 = b^-1 = 1/b

Potem je B = 5 in iskana funkcija je:

y = 5^x

Reference

1. Figuera, j. 2000. Matematika 1. Raznovrstno. Co-Bo izdaje.
2. Gid Hoffmann, J. Izbira vprašanj matematike za 4. Leto. Ed. Sphinx.
3. Jiménez, r. 2008. Algebra. Dvorana Prentice.
4. Larson, r. 2010. Izračun spremenljivke. 9na. Izdaja. McGraw Hill.
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.