Zmanjšanje funkcije, kako jo prepoznati, primeri, vaje

A zmanjšanje funkcije F je tisti, katerega vrednost se zmanjšuje, ko se vrednost x povečuje. Pomeni, da v določenem intervalu upoštevamo dve vrednosti x₁ in x₂ takšen, da je x₁ < x₂, potem f (x₁)> f (x₂).

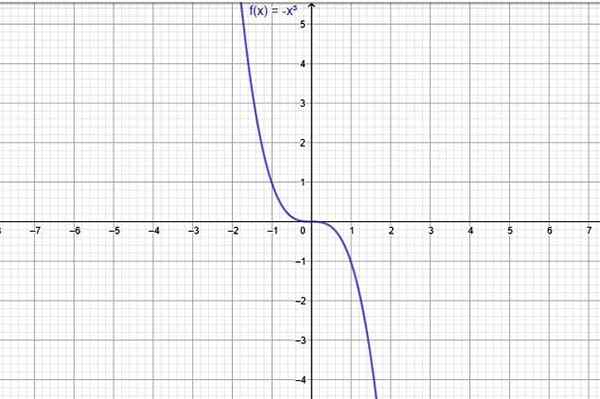
Primer funkcije, ki se vedno zmanjšuje, je f (x) = -x³, čigar graf prikazuje na naslednji sliki:

Slika 1. Funkcija, ki se v celotni domeni vedno zmanjšuje, je f (x) = -x^3. Vir: f. Zapata skozi Geogebro.

Čeprav je za nekatere funkcije, kot je ta, za vse svoje domene zmanjševanje, vse se ne obnašajo tako. Študija intervalov rasti in zmanjšanja se imenuje monotonost funkcije.

Prav tako se lahko na določeni domeni upošteva rast ali zmanjšanje funkcije. Toda vsaka funkcija, ki se v določenem intervalu zmanjšuje, je tudi na vsaki točki, ki ji pripada.

[TOC]

Kako prepoznati padajoče funkcijo?

Graf funkcije vizualno označuje, ali se zmanjšuje ali ne. Če se pri premikanju v naraščajočem smislu X funkcija "spušča", to pomeni, da se zmanjšuje.

In če imate intervale, v katerih se izmenično zmanjšuje in raste, kar je najbolj običajno, saj se to jasno razkriva z opazovanjem vedenja funkcije v celotni domeni, saj se bodo pojavili intervali, v katerih se funkcija "vzpenja" in drugi v ki se "spusti".

Če graf funkcije ni na voljo, je mogoče analitično ugotoviti, ali se v eni točki ali v intervalu zmanjšuje s prvim derivatom.

Merilo prvega izpeljanka

Upoštevajte vedenje zmanjšanja funkcije, prikazane na sliki 2. Segmenti roza črte so tangentni do točk, katerih koordinate so [a, f (a)in [A+H, F (A+H)] in imejte negativno naklon.

Vam lahko služi: Kako so informacije, pridobljene v anketi?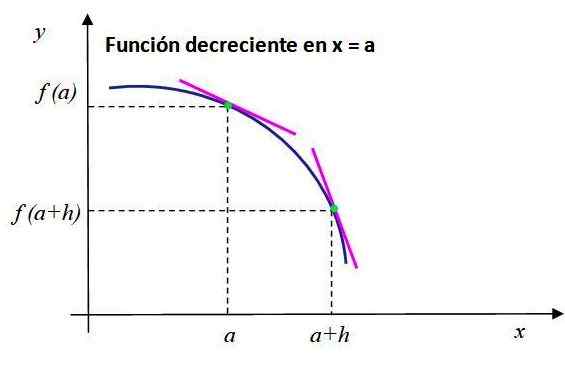Slika 2. Nagib tangentne črte na graf F (x) je negativen pri x = a, potem se funkcija v tej točki zmanjšuje. Vir: f. Zapata.

Za to funkcijo se izpolni naslednja:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Zato je mogoče misliti, da se funkcija zmanjšuje v x = a.

Vendar pa je prvi izpeljan iz funkcije f (x), ocenjeno pri x = a, ki je po definiciji naklon tangentne črte do krivulje pri x = a, podan z:

Omejitev kaže, da je vrednost H mogoče narediti tako majhno, kot želite, in nakazuje, da je znak fa), Uporablja se lahko za vedeti, ali se funkcija na določeni točki zmanjšuje ali ne, dokler v tem trenutku obstaja izpeljanka.

Potem ja fa) < 0, Lahko potrdimo, da se funkcija zmanjšuje, in nasprotno, če f '(a)> 0, Potem funkcija na tej točki raste.

Teorem za zmanjševanje in rastoče funkcije

Prej smo se sklicevali na obnašanje funkcije na neki točki. Zdaj naslednji izrek omogoča poznavanje intervalov, v katerih funkcija zmanjšuje, raste ali konstantna:

Naj bo F v intervalu različna funkcija (a, b). Res je, da:

-Da f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Če nasprotno f '(x)> 0 za vse x, ki pripada (a, b), se reče, da funkcija f (x) raste v (a, b).

-Končno, če je f '(x) = 0 za vse x, ki spada v interval (a, b), je f (x) v omenjenem intervalu konstanten.

Demonstracija

Recimo f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ in x₂ pripada omenjenemu intervalu in pogoju, da je x₁< x₂.

Teorem povprečne vrednosti navaja, da obstaja resnično število c, med x₁ in x₂, takšno, da:

Vam lahko služi: skupni dejavnik za razvrščanje izrazov: primeri, vaje

Kot je bilo ugotovljeno od x₁< x₂,  Δx je pozitiven. Torej, saj je f '(c) negativen, tako je tudi Δy. Zato f (x₁) je večji od f (x₂) In funkcija se v intervalu učinkovito zmanjša (a, b).

Koraki, da veste, ali se funkcija zmanjšuje

Za iskanje intervalov zmanjšanja in rasti funkcije z uporabo prejšnjega izrekanja sledimo tem korakom:

-Poiščite prvo, pridobljeno iz funkcije, in ga ujemajte z ničlo, pri čemer rešite tako. Določite tudi točke, na katerih derivat ne obstaja.

Vse te točke se imenujejo kritične točke In jih je treba najti, saj ima v njih derivat možnost spremeniti svoj znak, kar kaže na to, da funkcija prehaja iz rasti na zmanjšanje ali nasprotno.

-Domena funkcije je razdeljena na intervale, določene s točkami, na katerih je preklican prvi izpeljanka ali ne obstaja.

-Nazadnje se znak derivata preuči na poljubni točki, ki spada v vsakega od intervalov, pridobljenih v prejšnjem koraku.

Primeri zmanjšanja funkcij

Funkcije se ne zmanjšujejo z isto hitrostjo, nekatere to počnejo hitreje kot druge. Naslednje funkcije, ki se pogosto pojavljajo v praksi, se zmanjšujejo:

Eksponentna funkcija

Funkcija oblike f (x) = a^x, Z med 0 in 1, ki ne vključujejo teh, se hitro zmanjša v celotni njihovi domeni.

Funkcija 1/x

Preko spletnega grafičnega programa kot geogebre je zgrajen graf funkcije f (x) = 1/x, ki potrjuje, da se v celotni domeni zmanjšuje.

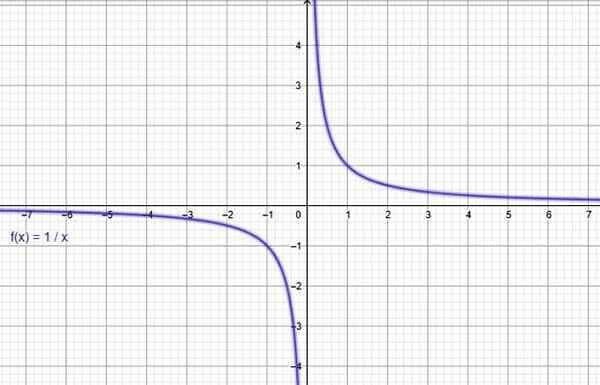Slika 3. Funkcija f (x) = 1/x se zmanjšuje. Vir: f. Zapata skozi Geogebro.

Povezana funkcija

Funkcije obrazca y = mx + b z m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Vam lahko služi: matematična enakost

Vaja rešena

Poiščite, če obstajajo, znižani intervali funkcije:

f (x) = x⁴ - 6x² - 4

Rešitev

Prvi korak je najti f '(x):

f '(x) = 4x³ - 12x

Prva derivat F (x) je neprekinjena funkcija, torej nima točk prekinitve, vendar je preklican v:

4x³ - 12x = 0 = 4x (x²-3) = 0

Rešitve te enačbe so: x₁ = 0, x₂ = - √3 in x₃ = √3. To so kritične točke, ki v intervalih delijo domeno f (x): (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Nato se oceni prvi izpeljan v poljubni vrednosti x, ki spada v vsak interval. Te vrednosti so bile izbrane:

Za (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Za (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Za (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Za (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Kot je več intervalov, je dobro narediti tabelo za organizacijo rezultatov. Puščica navzgor kaže, da funkcija raste in upada, kar se zmanjšuje:

Ugotovljeno je, da se funkcija v intervalih zmanjšuje (-∞,- √3) in (0, √3) in raste v preostalih intervalih. Prvotna funkcija v geogebri se zlahka preveri z grafikonom.

Reference

1. Ayres, f. 2000. Izračun. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Izračun z analitično geometrijo. Harla, s.Do.
3. Purcell, e. J., Varberg, d., & Rigdon, s. In. (2007). Izračun. Mehika: Pearson Education.
4. Matemobile. Funkcije, raste, zmanjšuje in konstantno. Okreval od: matemovil.com
5. Stewart, J. 2006. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.