Bijektivna funkcija Kaj je, kako je, primeri, vaje
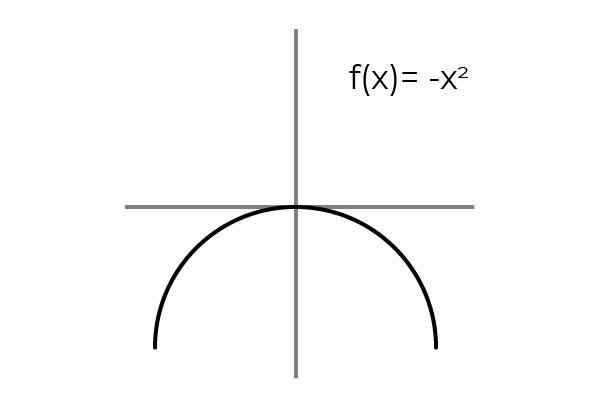
- 2939
- 648
- Cary Goyette
A Bijektivna funkcija To je tisti, ki izpolnjuje dvojni pogoj biti Injektivno in pretirano. To pomeni, da imajo vsi elementi domene eno samo sliko v kodominiju, zato je kodominium enak območju funkcije ( RF ).
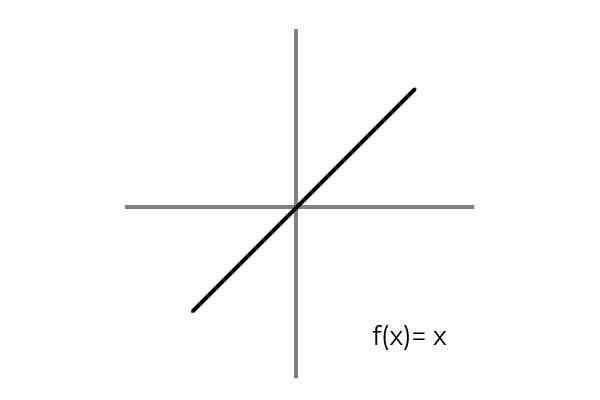
Izpolnjeno je, ko upošteva biunivokalno razmerje med elementi domene in kodominija. Preprost primer je funkcija F: r → R definirana s črto F (x) = x
 Vir: Avtor
Vir: Avtor Opažamo, da je za vsako vrednost domene ali nabora odhoda (oba izraza veljata enako) v kodominiju ali nastavitvi prihoda ena sama slika. Poleg tega ni elementa kodominija, ki ni slika.
Tako F: r → R definirana s črto F (x) = x je bijektiven
[TOC]
Kako je bijjektivna funkcija?
Če želite odgovoriti na to, je treba imeti jasne koncepte, povezane z Injektivnost in Prekomernost funkcije, Poleg meril za kondicioniranje funkcij, da jih prilagodimo zahtevam.
Injektivnost funkcije
Funkcija je Injektivno Ko je vsak element svoje domene povezan z enim samim elementom kodominija. Element kodominija je lahko le slika enega samega elementa domene, na ta način vrednosti odvisne spremenljivke ni mogoče ponoviti.
Razmisliti Injektivno Naslednje je treba izpolniti funkcijo:
∀ x1 ≠ x2 ⇒ F (x1 ) ≠ f (x2 )
Prekomernost funkcije
Funkcija je razvrščena kot Pretirano, Če je vsak element njegovega kodominija slika vsaj enega domenskega elementa.
Razmisliti Pretirano Naslednje je treba izpolniti funkcijo:
Vam lahko služi: nadomestno vzorčenjeBiti F: dF → CF
∀ B ℮ CF In do ℮ DF / F (a) = b
To je algebrski način, da ugotovimo, da za vsak "B", ki spada v CF Obstaja "A", ki pripada DF tako, da je funkcija, ocenjena v "a", enaka "B".
Kondicioniranje funkcij
Včasih funkcija, ki ni Bijective, lahko podvrže določeni kondiciji. Ti novi pogoji lahko to spremenijo v Bijektivna funkcija. Vse vrste sprememb domene in kodominija funkcije so veljavne, kjer je cilj izpolniti injektivnost in prekomerne lastnosti v ustreznem razmerju.
Primeri: rešene vaje
Vaja 1
Biti funkcija F: r → R definirana s črto F (x) = 5x +1
O: [Vse resnične številke]
Opazimo, da za katero koli vrednost domene obstaja slika v kodominiju. Ta slika je edinstvena, kar naredi F biti eden Injektivna funkcija. Na enak način opažamo, da je kodominium funkcije enak njegovemu območju. Tako izpolnjevanje pogoja Pretiranost.
Ker smo injektivni in pretirani, hkrati lahko sklepamo
F: r → R definirana s črto F (x) = 5x +1 je Bijektivna funkcija.
To velja za vse linearne funkcije (funkcije, katerih večja stopnja spremenljivke je ena).
Vaja 2
Biti funkcija F: r → R definirano s F (x) = 3x2 - 2
Pri risanju vodoravne črte opazimo, da graf najdemo večkrat. Zaradi tega je funkcija F Ni injektiven in zato ne bo Bijective Medtem ko je opredeljen v R → R
Na enak način obstajajo vrednosti kodominija, ki niso slike nobenega elementa domene. Zaradi tega funkcija ni prekomerna, kar je tudi zaslužno za pogoj nabora prihoda.
Vam lahko služi: teorija nastavitve: značilnosti, elementi, primeri, vajeDomena in kodominium funkcije je pogojena
F: [0 , ∞] → [ - 2 , ∞ ]
Kjer opazimo, da nova domena pokriva vrednosti od nič do pozitivne neskončnosti. Izogibanje ponovitvi vrednosti, ki vpliva na injektivnost.
Tako je bil kodominium spremenjen, odšteva se od "-2" v pozitivno neskončnost, ki iz kodominija izloči vrednosti, ki niso ustrezale nobenemu domenskemu elementu
Na ta način je mogoče zagotoviti F : [0 , ∞] → [ - 2 , ∞ ] definirano s F (x) = 3x2 - 2
Je bijektivno
Vaja 3
Biti funkcija F: R → R definirano s F (x) = greh (x)
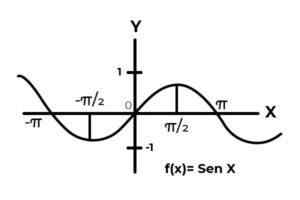
V intervalu [ -∞ , +∞ ] Funkcija sinusa spreminja svoje rezultate med ničlo in eno.
 Vir: Avtor.
Vir: Avtor. Funkcija F Ne ustreza kriterijem injekcije in prekomernosti, ker se odvisne spremenljive vrednosti ponavljajo vsak π interval. Poleg tega pogoji kodominija zunaj intervala [-eleven] Niso podoba nobenega domenskega elementa.
Pri preučevanju grafike funkcije F (x) = greh (x) intervali opazimo, kjer vedenje krivulje izpolnjuje merila Bijektivnost. Kot je interval DF = [ π/2,3π/2 ] Za domeno. In CF = [-1, 1] Za kodominium.
Kjer se funkcija razlikuje od 1 do -1, ne da bi v odvisni spremenljivki ponavljali kakršno koli vrednost. In hkrati je co -oominium enak vrednostim, ki jih je sprejel izraz Greh (x)
Na ta način je funkcija F: [ π/2,3π/2 ] → [-1, 1] definirano s F (x) = greh (x). Je bijektivno
Vaja 4
Povečati potrebne pogoje za DF in cF. Tako da je izraz
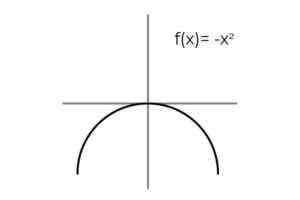
Lahko vam služi: Napaka vzorčenja: formule in enačbe, izračun, primeriF (x) = -x2 Biti bikcije.
 Vir: Avtor
Vir: Avtor Ponavljanje rezultatov opazimo, ko spremenljivka prevzame nasprotne vrednosti:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = f (-4) = -16
Domena je kondicionirana in jo omejuje na desno stran prave črte.
DF = [0 , +∞ ]
Na enak način je opaziti, da je obseg te funkcije interval [ -∞ , 0, ki s kodominijem izpolnjuje pogoje prekomernosti.
Na ta način lahko to sklepamo
Izraz F: [0 , +∞ ] → [ -∞ , 0 definirano s F (x) = -x2 Je bijektivno
Predlagane vaje
Preverite, ali so naslednje funkcije Bijective:
F: [0 , ∞) → R definirano s F (x) = 3 (x + 1)2 +2
F: [ 3π/2,5π/2 ] → R definirano s F (x) = 5ctg (x)
F: [ -π,π ] → R definirano s F (x) = cos (x - 3)
F: r → R definirana s črto F (x) = -5x + 4
Reference
- Uvod v logiko in kritično razmišljanje. Merrilee h. Losos. Univerza v Pittsburghu
- Težave v matematični analizi. Piotr Bilar, Alfred Witkowski. Univerza v Wroclawu. Palica.
- Elementi abstraktne analize. Mícheál o'searcoid doktorat. Oddelek za matematiko. University College Dublin, Beldfield, Dublind 4
- Uvod v logiko in metodologijo deduktivnih znanosti. Alfred Tarski, New York Oxford. Oxford University Press.
- Načela matematične analize. Enrique Linés Escardó. Uredništvo Reverté s. Do leta 1991. Barcelona, Španija.
- « Glikogenska struktura, sinteza, razgradnja, funkcije
- Značilne značilnosti encimov, mehanizmi akcije, primeri »

