Faktoring

Kaj je faktorizacija?

Faktorizacija je metoda, s katero se izraža polinom v obliki množenja dejavnikov, ki so lahko številke, črke ali oboje. Za dejavnik so dejavniki, ki so skupni izrazom, razvrščeni in na ta način se polinom razgradi v več polinomov.

Torej, ko se dejavniki med seboj pomnožijo, je rezultat prvotni polinom. Faktorizacija je zelo uporabna metoda, kadar obstajajo algebrski izrazi, saj lahko postane množenje več preprostih izrazov; Na primer: 2² + 2ab = 2a _* (A + B).

Obstajajo primeri, v katerih polinoma ni mogoče upoštevati, ker med njegovimi izrazi ni skupnega dejavnika; Tako so ti algebrski izrazi deljivi le med seboj in 1. Na primer: x + y + z.

V algebrskem izrazu je skupni faktor največji skupni delilnik izrazov, ki ga sestavljajo.

Metode faktorizacije

Obstaja več faktorizacijskih metod, ki se uporabljajo odvisno od primera. Nekateri od teh so naslednje:

Skupna faktorizacija

V tej metodi so opredeljeni tisti dejavniki, ki so običajni; torej tisti, ki se ponavljajo v izrazu. Nato se uporabi distribucijska lastnost, največji skupni delitelj se odstrani in faktorizacija zaključi.

Z drugimi besedami, identificiran je skupni dejavnik izraza in vsak izraz je razdeljen med to; Nastali izrazi bo pomnožen z največjim skupnim delilnikom za izražanje faktorizacije.

Primer 1

Faktorizira (b²x) + (b²in).

Rešitev

Prvi je skupni dejavnik vsakega izraza, ki je v tem primeru b², In potem so izrazi razdeljeni med skupni faktor na naslednji način:

(b²x) / b² = x

(b²y) / b² = y.

Faktorizacija je izražena in pomnoži skupni dejavnik z dobljenimi izrazi:

(b²x) + (b²y) = b² (x + y).

Primer 2

Faktorizirajte (2. mesto²b³) + (3ab²).

Rešitev

V tem primeru imamo dva dejavnika, ki se ponavljata v vsakem izrazu, ki sta "A" in "B", in ki sta dvignjeni na oblast. Da bi jih najprej upoštevali, sta dva izraza razčlenjena v dolgi obliki:

2_*do_*do_*b_*b_*B + 3a_*b_*b

Vidimo, da se faktor "a" ponavlja samo enkrat v drugem mandatu, faktor "B" pa se v tem ponovi dvakrat; Torej je v prvem mandatu le 2, faktor "a" in en "b"; Medtem ko v drugem mandatu ostane le še 3.

Zato je napisan tolikokrat, kolikor se "A" in "B" ponavljajo in pomnožijo s dejavniki, ki so ostali iz vsakega izraza, kot je opaziti na sliki:

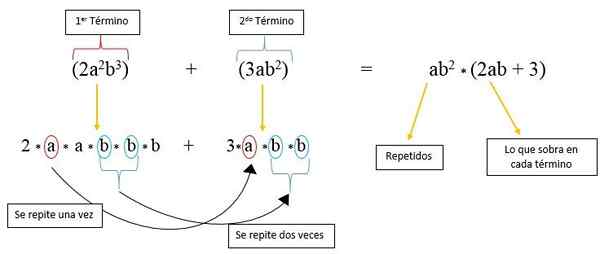
Faktorizacija združevanja

Ker ni v vseh primerih najvišji skupni delitev polinoma, je jasno izražen, je treba narediti druge korake, da lahko prepišete polinom in tako faktoriziramo.

Vam lahko služi: stožčasti odseki: vrste, aplikacije, primeri

Eden od teh korakov je razvrstitev izrazov polinoma v več skupin in nato uporabiti metodo skupne faktorje.

Primer 1

Faktorizirajte AC + BC + AD + BD.

Rešitev

Obstajajo 4 dejavniki, pri katerih sta dva pogosta: v prvem mandatu je "C", v drugem pa "D". Tako sta oba izraza združena in ločena:

(AC + BC) + (AD + BD).

Zdaj je mogoče uporabiti skupno faktorsko metodo, ki vsak izraz deli po skupnem faktorju in nato pomnoži ta skupni faktor z dobljenimi izrazi, kot je ta:

(AC + BC) / C = A + B

(ad + bd) / d = a + b

C (A + B) + D (A + B).

Zdaj dobimo binom, ki je pogost za oba izraza. Za faktor ga pomnoži preostali dejavniki; Tako morate:

AC + BC + AD + BD =  (C + D) _* (A + B).

Inšpekcijska faktorizacija

Ta metoda se uporablja za faktor kvadratnih polinomov, imenovanih tudi trinomiji; torej tisti, ki so strukturirani kot sekira² ± BX + C, kjer je vrednost "A" drugačna od 1. Ta metoda se uporablja tudi, kadar ima trinomial obliko x² ± bx + c in vrednost "a" = 1.

Primer 1

Faktor x² + 5x + 6.

Rešitev

Imate kvadratni trinomial oblike x² ± bx + c. Najprej je treba ugotoviti dve številki, ki pri pomnožitvi povzroči vrednost "C" (to je 6) in da je njegova vsota enaka koefiku "B". Te številke sta 2 in 3:

2 _* 3 = 6

2 + 3 = 5.

Na ta način je izraz poenostavljen na naslednji način:

(x² + 2x) + (3x + 6)

Vsak izraz je dejavnik:

• Za (x² + 2x) Skupni izraz se odstrani: x (x + 2)
• Za (3x + 6) = 3 (x + 2)

Tako izraz ostane:

x (x +2) +3 (x +2).

Ker imate skupni binom, da zmanjšate izraz, to pomnoži z ostanki in mora:

x² + 5x + 6 = (x + 2) _* (x + 3).

Primer 2

Faktorizirajte 4a² + 12A +9 = 0.

Rešitev

Imate kvadratni trinomial oblike sekire² ± bx + c in za upoštevanje pomnoži ves izraz s koeficientom x²; V tem primeru 4.

4² + 12A +9 = 0

4² (4) + 12A (4) + 9 (4) = 0 (4)

16 a² + 12A (4) + 36 = 0

4² do² + 12A (4) + 36 = 0

Zdaj je treba ugotoviti dve številki, da pri množitvi med seboj povzroči vrednost "C" (kar je 36) in da pri združevanju koeficienta izraza "A", ki je 6.

6 _* 6 = 36

6 + 6 = 12.

Tako je izraz prepisan, ob upoštevanju tega 4² do² = 4a _* 4. Zato se za vsak izraz uporablja distribucijska lastnost:

Vam lahko postreže: Mackinder Box

(4A + 6) _* (4A + 6).

Končno je izraz razdeljen s koeficientom a²; to je 4:

(4A + 6) _* (4A + 6) / 4 = ((4A + 6) / 2) _* ((4A + 6)/ 2).

Izraz je naslednji:

4² + 12A +9 = (2A +3) _* (2A + 3).

Faktorizacija z pomembnimi izdelki

Obstajajo primeri, v katerih v celoti upoštevamo polinome s prejšnjimi metodami, postane zelo dolg proces.

Zato je mogoče razviti izraz s formulami pomembnih izdelkov, zato postopek postane enostavnejši. Med najbolj uporabljenimi pomembnimi izdelki so:

• Razlika dveh kvadratov: (a² - b²) = (a - b) _* (A + B)
• Popoln kvadrat vsote: a² + 2ab +b² = (A + B)²
• Popoln kvadrat razlike: a² - 2ab + b² = (A - B)²
• Razlika dveh kock: a³ - b³ = (A-B)_*(do² + AB + b²)
• Vsota dveh kock: a³ - b³ = (A + B) _* (do² - AB + b²)

Primer 1

Faktorizira (5² - x²)

Rešitev

V tem primeru obstaja razlika dveh kvadratov; Zato se uporablja formula pomembnega izdelka:

(do² - b²) = (a - b) _* (A + B)

(5² - x²) = (5 - x) _* (5 + x)

Primer 2

Faktorizirajte 16x² + 40x + 25²

Rešitev

V tem primeru je popoln kvadrat vsote, ker je mogoče prepoznati dva kvadratna izraza, in izraz, ki je ostal, je rezultat pomnoževanja dveh s kvadratnim korenom prvega mandata s kvadratnim korenom drugega mandata.

do² + 2ab +b² = (A + B)²

Za faktor se izračunajo samo kvadratne korenine prvega in tretjega izraza:

√ (16x²) = 4x

√ (25²) = 5.

Nato sta oba nastala izraza izražena ločena z znakom operacije in ves kvadratni polinom je povišan:

16x² + 40x + 25² = (4x + 5)².

Primer 3

Faktorizirajte 27A³ - b³

Rešitev

Izraz predstavlja odštevanje, v katerem sta dva dejavnika povišana na kocko. Če jih želite upoštevati, se uporablja formula pomembnega izdelka razlike v kockah, kar je:

do³ - b³ = (A-B)_*(do² + AB + b²)

Tako se za faktor kubični koren odstrani iz vsakega izraza binoma in pomnoži s kvadratom prvega mandata, skupaj z izdelkom prvega do drugega mandata, plus drugi izraz kvadrat.

27a³ - b³

³√ (27a³) = 3a

³√ (-b³) = -b

27a³ - b³ = (3a - b) _* [(3a)² + 3ab + b²)

27a³ - b³ = (3a - b) _* (9a² + 3ab + b²)

Faktorizacija s pravilom Ruffini

Ta metoda se uporablja, če imate polinom stopnje večje od dveh, da se izraz poenostavi na več manjših polinomov.

Primer 1

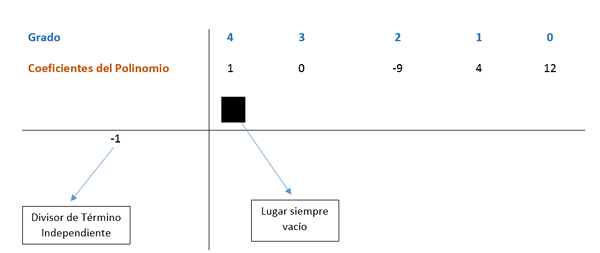
Faktorice q (x) = x⁴ - 9x² + 4x + 12

Rešitev

Najprej se iščejo številke, ki so delitve 12, kar je neodvisen izraz; Ti so ± 1, ± 2, ± 3, ± 4, ± 6 in ± 12.

Vam lahko služi: večkratniki 2: kaj so in razlaga

Potem se X nadomesti s temi vrednosti, od najmanj do največjih, in tako je določeno s tem, katero od vrednosti bo delitev natančna; Se pravi, ostalo mora biti 0:

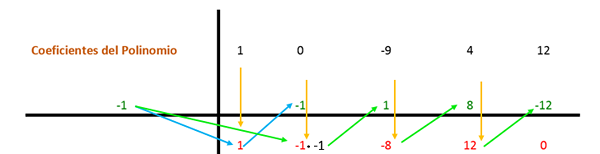
x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

In tako naprej za vsakega delilnika. V tem primeru so najdeni dejavniki za x = -1 in x = 2.

Zdaj se uporablja metoda Ruffini, v skladu s katero bodo koeficienti izražanja razdeljeni z najdenimi dejavniki, tako da je delitev natančna. Polinomni izrazi so naročeni od večjega do nižjega eksponenta; V primeru, da izraz manjka s stopnjo, ki sledi v zaporedju, je 0 postavljen.

Koeficienti se nahajajo v shemi, kot je prikazano na naslednji sliki.

Prvi koeficient zniža in pomnoži delitelj. V tem primeru je prvi delilnik -1, rezultat pa je postavljen v naslednji stolpec. Nato se vrednost koeficienta s tem dobljenim rezultatom doda navpično in rezultat je postavljen spodaj. Tako se postopek ponovi do zadnjega stolpca.

Potem se isti postopek ponovi, vendar z drugim delilnikom (ki je 2), ker je izraz še vedno mogoče poenostaviti.

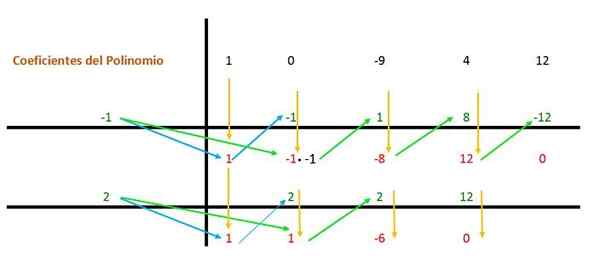
Tako bo imel za vsak koren, ki je bil dosežen, polinom izraz (x - a), kjer je "a" vrednost korena:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Po drugi strani bi morali te izraze pomnožiti ostali, ki so ostali iz pravila Ruffini 1: 1 in -6, ki so dejavniki, ki predstavljajo diplomo. Na ta način je izraz: (x² + X - 6).

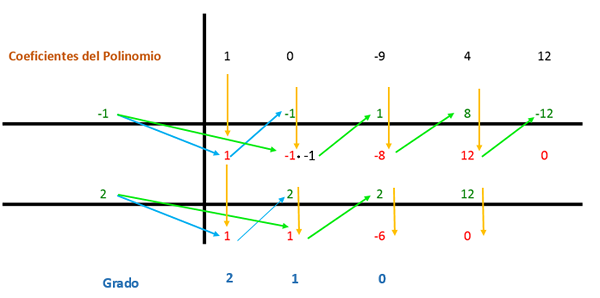
Pridobivanje rezultata polinomne faktorizacije z Ruffinijevo metodo je:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Končno je polinom stopnje 2, ki se pojavi v prejšnjem izrazu, napisati kot (x+3) (x-2). Zato je končna faktorizacija:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Reference

1. Arthur Goodman, L. H. (devetnajst devetdeset šest). Algebra in trigonometrija z analitično geometrijo. Pearson Education.
2. J, v. (2014). Kako učiti otroke o faktorju polinoma.
3. Manuel Morillo, a. S. (s.F.). Osnovna matematika z aplikacijami.
4. Roelse, str. L. (1997). Linearne metode za polinomno faktorizacijo na končnih poljih: teorija in izvedbe. University Essen.
5. Sharpe, d. (1987). Obroči in faktorizacija.