Konveksno ogledalo

Kaj je konveksno ogledalo?

On Konveksno ogledalo Ali Divergent je ukrivljeno ogledalo, skoraj vedno sferično in z odsevno površino na zunanji strani krogle, kot so okraski božičnega drevesa. Zahvaljujoč konveksnim ogledalom je mogoče.

Na primer, ogledala, ki so nameščena na ulicah, da olajšajo prehod vozil v ozkih križih.

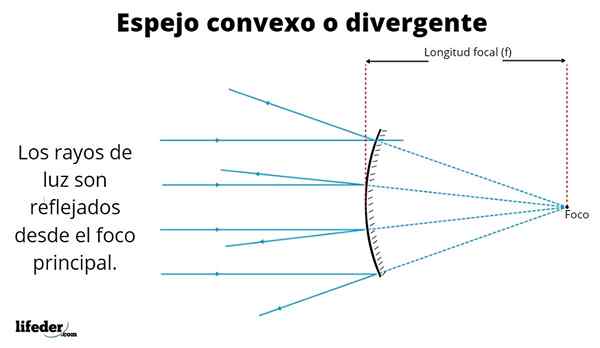
Ilustracija konveksnega ogledala

Tako oblikovane slike so raznolike, odvisno od mesta, kjer je predmet postavljen. Vrhunska slika prikazuje vzporedne žarke iz oddaljenega vodnjaka, kot je sonce.

Žarki se odražajo v skladu z refleksnim zakonom, kar kaže, da je kot pojavnost strele enaka, s katero se odraža. Kot lahko vidimo, so odsevni žarki ločeni - ne prečkajo - ko zapustijo spekularno površino, zato je tovrstno ogledalo znano tudi kot divergentno.

Ko se odsevi razširijo od ogledala - prekinitvene črte na sliki - te sekajo v točki, imenovani fokus.

Značilnosti konveksnih ogledal

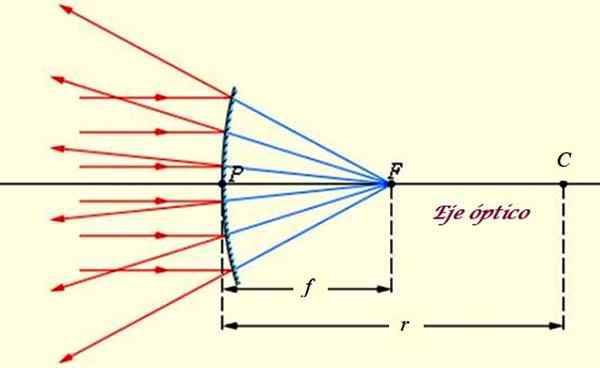Konveksno ali divergentno ogledalo, na katerem vplivajo žarki oddaljenega vodnjaka, kot je sonce. Vir: f. Zapata.

Konveksno ogledalo ima naslednje značilnosti (glej vrhunsko sliko):

-Pomembne točke ogledala so:

• C Središče, ki sovpada s sredino sfere, kamor spada ogledalo.
• F Osredotočenost, kjer se žarki odražajo za ogledalom.
• Vertex p istega, ki ustreza središču sferične površine in je kolinealno s C in F.

Vam lahko služi: ío (satelit)

-Ima Optična os tudi glavna os, ki je črta, pravokotna na spekularno površino. Žarki, ki vplivajo na optično osi, se odražajo v isti smeri.

-Središče sfere, ki ji pripada ogledalo, je v točki C in R je njegov polmer. A C je znan kot Ukrivljenost, medtem r Je on Polmer ukrivljenosti in označuje, kako ukrivljeno je ogledalo: mladoletnik r, bolj poudarjena je konveksna oblika.

-Presečiščena točka odsevnih žarkov je znana kot Žariščna točka ogledala. Razdalja med F in P je približno r/2:

F = r/2

Ta izraz velja za ogledala, katerih velikost je precej nižja od polmera ukrivljenosti.

-Slika, ki se oblikuje, je manjša in tudi virtualna, saj se nahaja za ogledalom, kot bomo videli naslednje.

Oblikovanje slike v konveksnem ogledalu

Vedeti, kako je slika, ki je nastala v konveksnem ogledalu, obdelava žarkov, ki je sestavljena iz predstavitve svetlobnih žarkov.

Ti žarki se odražajo na površini ogledala in narisani so tudi odsevni žarki. Metoda žarkov je uporabna za kakršno koli ogledalo, ne le izbokline.

S podaljšanjem odsevnih žarkov se sekajo v določeni točki in prav tam, kjer se slika oblikuje. Razširitev odsevnih žarkov, ki prihajajo iz razširjenega predmeta kot drevo.

Na spodnji sliki so narisani trije žarki iz predmeta, zelo posebne in enostavne za risanje, pa tudi njegove odseve:

Vam lahko služi: toplotna dilatacija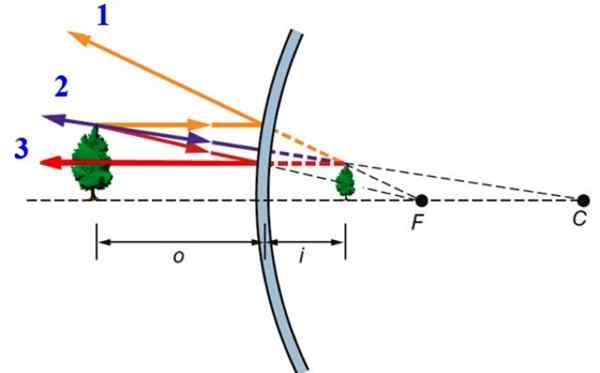 Slika 2.- Oblikovanje slike v konveksnem ogledalu. Vir: f. Zapata.

-Ray 1, ki vpliva vzporedno z optično osi.

-Ray 2, ki vpliva na eksolitacijo odsevnega žarka, prehaja natančno skozi žarišče ogledala, torej točka F. Ta žarek se odraža vzporedno z optično osi.

-Končno Ray 3, ki pravokotno sega na sferično površino, zato se odraža v isti smeri.

Načeloma ta postopek velja za vsako točko drevesa, toda s podatki, pridobljenimi iz treh narisanih žarkov.

Primeri in uporabe konveksnih ogledal

Številne zelo vlečene sferične površine delujejo kot konveksna ogledala, na primer svetle in srebrne božične okraske, pa tudi nove in svetle jeklene žlice.

Tudi konveksna ogledala imajo veliko praktičnih aplikacij, na primer:

Ogledala za preprečevanje prometnih nesreč

Konveksna ogledala na ulicah in avenijah pomagajo preprečiti nesreče, saj vam omogočajo, da vidite promet, ki prihaja iz kotičkov.

Nadzorna ogledala

V trgovinah in bankah so običajno konveksna ogledala za odkrivanje tatov, pa tudi, da se izognemo trkom med ljudmi in vozili za viličarje, ki krožijo v dvoranah in med policami.

Ogled vzvratnih ogledal

Avtomobili in motocikli imajo konveksna ogledala, ki proizvajajo nekoliko manjše slike, vendar pokrivajo več vidnega polja kot ravna ogledala.

Cassegrain teleskop

Eno od ogledal reflektorja Cassegraina, sekundarnega ogledala, je izbočen, čeprav ni sferičen in služi za odsev slike proti glavnemu ogledalu teleskopa.

Vam lahko služi: gravitacijska energija: formule, značilnosti, aplikacije, vaje

Konveksne zrcalne enačbe

Razmislite o pravokotnikih naslednje slike, ki ga določa Ray 1, ki prihaja z vrha puščice, njegovega odseva in razširitve tega.

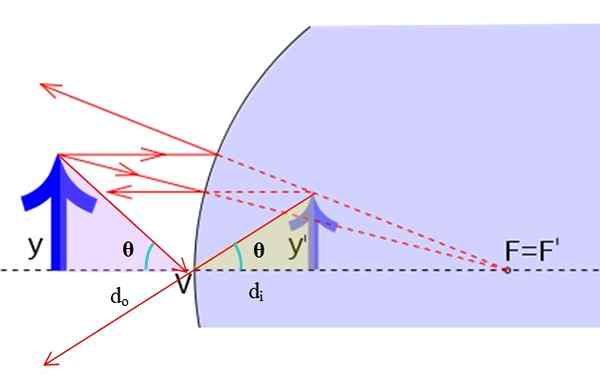Geometrija, da bi našli povečavo ogledala. Vir: f. Zapata.

Prvotna slika ima višino in, medtem ko je višina virtualne slike in ' . Res je, da:

Tan θ = y/d_tudi = Y '/d_Yo

Povečanje ogledala

Razlog med višino slike in višino predmeta je Povečanje ogledala, To se imenuje, tudi če je pridobljena slika manjša od pravega predmeta. Označujemo ga m:

M = y '/ y = d_Yo /d_tudi

Razmerje med predmetom in njegovo sliko v konveksnem ogledalu

Zdaj pa razmislimo o tej drugi številki, kjer lahko območje AVF približno obravnavamo kot pravi trikotnik, saj ukrivljenost ogledala ni zelo izrazita. Zato:

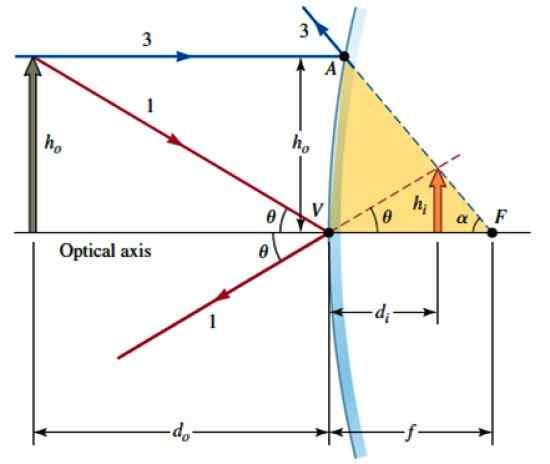Geometrija za iskanje matematičnega odnosa med predmetom in njegovo podobo. Vir: Katz, D. Fizika za znanstvenike in inženirje.

Av ≈ h_tudi

Tako:

Tan α = h

Zato:

Inverzno od tega izraza je povečava, potem pa:

Zato:

1- (d_Yo /f) = D_Yo /d_tudi

Z delitvijo vsega med D_Yo:

Končno:

 Zdaj za ogledala veljajo nekateri znaki. Čeprav vemo, da je razdalja vedno pozitivna, se na vseh razdaljah za ogledalom loči z negativnim znakom.

Zato kot F in d_Yo So za ogledalom, postavljeni so manjši, medtem ko za razdaljo d_tudi To ni potrebno, saj je pred ogledalom. Tako ostaja prejšnja enačba:

Lahko je dokazano, da ta enačba velja tudi za konkavno ogledalo.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 2. MC Graw Hill.
2. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
3. Katz, d. 2017. Fizika za znanstvenike in inženirje. Cengage učenje.
4. Thomas, w. 2008. Konceptualna fizika. McGraw Hill.
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.