Formula in enačbe napetostni napor, izračun, vaje

On Napetostni obremenitev Opredeljen je kot sila, pravokotna na območje na območju enote, ki se na njenem konci. Njegove dimenzije so sile / območja in v matematični obliki ga lahko izrazimo na naslednji način:

τ = f / a

Enotnost truda v mednarodnem sistemu enot je enaka, ki se uporablja za pritisk: Pascal, skrajšana PA, ki je enakovredna 1 Newtonu/ M².

Slika 1. Če napetostni napor presega določeno vrednost, se vrv poruši. Vir: pxhere.

V napetostnih prizadevanjih obstajata dve sili, ki se uporabljata v isti smeri in nasprotna čutila, ki raztegnejo telo. Če je bila prvotno dolžina predmeta l_tudi, Pri uporabi napetosti je nova dolžina L, raztezanje ΔL pa se izračuna z:

Δl = l - l_tudi

Trdni predmeti imajo elastičnost v večji ali manjši meri, kar pomeni, da se, ko napetostni napori izginejo, vrnejo v svoje prvotne dimenzije.

To se zgodi pod pogojem, da trud ni tako velik, da bi povzročil trajno deformacijo. Gumijasti, gumijasti ali gumijasti materiali so dobri za elastične predmete in imajo tudi to kakovostne lase in kožo.

[TOC]

Enotna deformacija

Pri preučevanju, kako so telesa deformirana pod napetostjo, je zelo priročno določiti koncept Enotna deformacija, Sproščena količina. Enotno deformacijo je označena z grško črko δ (mala črka "delta") in se izračuna na naslednji način:

Δ = ΔL /L_tudi

Enotna deformacija služi za primerjalno oceno deformacije predmeta pod napetostjo. Poglejmo ga na ta način: ni enako raztezanju 1 cm palice dolge 1 metra, da se raztegne 1 cm do še 10 m dolge. V prvem primeru je deformacija veliko pomembnejša kot v drugem.

Lahko vam služi: ohm: Odpornost, primeri in rešeni vaja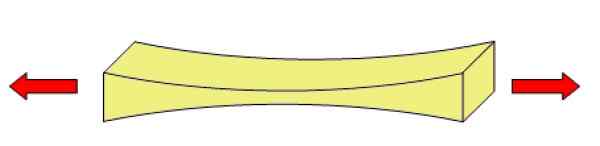Slika 2. Predmet, ki je podvržen napetosti ali oprijemanju, je deformiran. Vir: Wikimedia Commons.

Kako se izračuna napetost? (Primeri)

Newtonov angleški in sodobni fizik z imenom Robert Hooke (1635-1703), raziskal elastične lastnosti teles in vzpostavil zakon, ki nosi njegovo ime. Z njim je napor, ki se uporablja za deformacijo, ko je napor majhen, povezan:

Napor ∝ deformacija (Unital)

Logično je pričakovati, da bo večji stresni napori, večje podaljšanje. Uporaba zgoraj navedenih definicij:

τ ∝ δ

Konstanta sorazmernosti, potrebna za določitev enakosti, je označena in je znana kot mladi modul ali elastičnost, značilen za materiale:

τ = y⋅δ

Young's modul ima enake enote napetosti, saj je deformacija enote brezdimenzionalna.

Torej, način za izračun stresnega truda v telesu z elastičnimi lastnostmi, merjenje deformacije in poznavanja njegovega mladega modula. Ta znesek je bil eksperimentalno določen za številne materiale in je tabela.

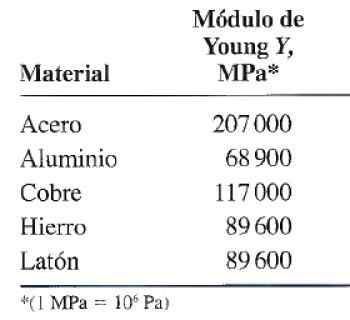Slika 3. Tabela Young's Elastity ali Modul Modul za nekaj običajnih materialov. Vir: Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne.

Primer izračuna

Recimo, da je jeklo s kaljenim premerom 3 mm podvrženo napetosti, ki od njega obesi težo 250 n, kakšna bi bila velikost omenjenega truda?

No, definicijo napetosti lahko uporabimo kot količnik med silo, pravokotno na površino in območjem omenjene površine. Najprej izračunajmo območje, ob predpostavki krožne žice prereza:

Lahko vam služi: masna številka: kaj je to in kako ga dobiti (s primeri)

A = π . (D/2)² =  π . (d² /4)

Premer žice je 3 mm in te enote morajo biti preoblikovane v števce:

D = 3 x 10^-3 m.

A = π . (3 x 10^-3 m)² / 4 = 7.07 x 10^-6 m².

Napeto na napetosti nastane s težo, ki visi iz žice, ki se uporablja pravokotno na svoj presek, zato:

τ = 250 n / 7.07 x 10^-6 m² = 3.5 x 10 ⁷ Pa

Pascal je dokaj majhna enota, zato množice niso nenavadne. Vedeti, da je 1 mega-Pascal (MPA) 10⁶ Pascal, napetostni napori ostajajo:

τ = 35 MPa

Rešene vaje

- Vaja 1

Modul elastičnosti palice je 4 x 10^enajst Pa. Katera enota deformacija dobimo z uporabo napetostnega napora 420 MPA?

Rešitev

Enačba, ki jo je treba uporabiti, je:

τ = y⋅δ

Z njim izračunamo enotno deformacijo:

Δ = τ / y = 420 x 10⁶ PA/ 4 x 10^enajst Pa = 0.00105

Δ = ΔL /L_tudi

Zato je deformacija ΔL:

ΔL = 0.00105 l_tudi

Če je bila na primer palica prvotno dolga 1 meter, s tem napetostjo se razteza le 0.00105 M = 1.05 mm.

- Vaja 2

Jeklena žica ima 1.50 m dolg in premer 0.400 mm. Eden od koncev je pritrjen na streho, na drugo pa je nameščen množični reflektor m = 1.50 kg, ki je sproščeno. Izračunati:

a) Raztezanje žice.

b) enotna deformacija in odstotek enotne deformacije. Ali je mogoče, da je žica prekinjena s težo reflektorja?

Rešitev

Žica se bo raztegnila, saj je reflektor podvržen napetosti. Sila, ki jo povzroči ta prizadevanje, je teža reflektorja.

Lahko vam služi: fizika pred Grki (Antigua Grčija)

Teža masnega predmeta je produkt mase z vrednostjo pospeška gravitacije:

F = 1.50 kg x 9.8 m/s² = 14.7 n

Potreben je prerez odseka žice:

A =  π . (d² /4) = π x (0.4 x 10-3 m) 2 /4 = 1.26 x 10^-7 m².

S temi rezultati se izračuna napor na žici:

τ = 14.7 N / 1.26 x 10^-7 m² = 1.17 x 10⁸ Pa

Žica ima elastično vedenje, zato je veljavno domnevati, da je Hookejev zakon izpolnjen:

τ = y⋅δ

Iz tabele modula Elastity ugotovimo, da je za jeklo y = 207 x 10⁹ Pa. Poleg tega je enotna deformacija:

Δ = ΔL /L_tudi

Zamenjava v enačbi za trud:

τ = y⋅Δ = y⋅ (Δl /l_tudi)

Zato je raztezanje:

Δl = l_tudi τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ Pa = 8.5 x 10^-4 M = 0.849 mm.

Enotna deformacija žice je:

Δ = ΔL /L_tudi = 8.5 x 10^-4 m / 1.5 m = 5.652 x 10^-4

Če ga izrazimo kot odstotek, je odstotna enotna deformacija 0.0565 %, manj kot 0.1 %, zato se pričakuje, da se žica upira teži reflektorja brez zloma, saj deformacija, ki jo doživlja, ni prevelika v primerjavi s prvotno dolžino.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Pivo, f. 2010. Mehanika materialov. McGraw Hill. 5. Izdaja.
3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
5. Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne.