Določitev translacijskega stanja, aplikacije, primeri

On Translacijsko ravnovesje To je stanje, v katerem je predmet kot celota, ko so vse sile, ki delujejo nanj. Matematično je enakovredno reči, da je F₁+ F₂ +  F₃ +.. . = 0, biti f₁, F₂,  F₃... vpletene sile.

Dejstvo, da je telo v translacijskem ravnovesju, še ne pomeni, da je nujno v mirovanju. To je poseben primer prejšnje opredelitve. Predmet je lahko v gibanju, vendar v odsotnosti pospeška bo to enotno pravokotno gibanje.

Slika 1. Prevodno ravnovesje je pomembno za veliko število športov. Vir: Pixabay.

Torej, če se telo v mirovanju nadaljuje. In če že imate gibanje, bo imela konstantno hitrost. Na splošno je gibanje katerega koli predmeta sestava prevodov in rotacij. Prevodi so lahko prikazani na sliki 2: linearni ali krivo.

Če pa je ena od točk predmeta pritrjena, potem je edina možnost premika. Primer tega je CD, katerega središče je pritrjeno. CD se lahko vrti okoli osi, ki poteka skozi to točko, vendar se ne premikati.

Ko imajo predmeti fiksne točke ali so podprti na površinah, se govori povezave. Povezave medsebojno omejujejo gibe, ki jih je predmet sposoben narediti.

[TOC]

Določitev translacijskega ravnovesja

Za delček v ravnovesju je veljavno zagotoviti:

F_R = 0

Ali povzetek zapisa:

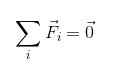
Jasno je, da mora biti telo v translacijskem ravnovesju, sile, ki delujejo nanj.

Na ta način objekt ne bo doživel pospeška in vsi njeni delci so v mirovanju ali eksperimentirajo pravokotne prevode s konstantno hitrostjo.

Lahko vam služi: Teorija velikega poka: značilnosti, stopnje, dokazi, problemi

Če se lahko predmeti obrnejo, bodo to na splošno storili. Zato večina gibov sestavlja kombinacije prevajanja in vrtenja.

Vrtenje predmeta

Ko je rotacijsko ravnovesje pomembno, bo morda treba zagotoviti, da se predmet ne obrne. Potem se morate preučiti, ali na to delujejo navori ali trenutki.

Navor je vektorska velikost, od katere so odvisne rotacije. Zahteva, da se uporabi sila, vendar je pomembna tudi uporaba tega. Če želite razjasniti idejo, razmislite o razširjenem predmetu, na katerem deluje sila F In poglejmo, ali lahko ustvarite rotacijo glede na neko osi oz.

Že je intuitirano, da s potiskanjem predmeta v točki P s silo F, Možno je obrniti točko O, s protiročno smerjo. Pomembna pa je tudi smer, v katero se uporablja sila. Na primer sila, uporabljena na sliki medija, predmeta ne bo mogla obrniti, čeprav ga zagotovo lahko premakne.

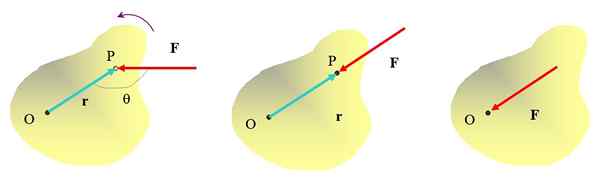Slika 2. Dobimo različne načine uporabe sile na obsežnem predmetu, le na sliki skrajnega levega učinka rotacije se dobijo. Vir: Self Made.

Uporabite silo neposredno na točki ali ne bo uporabljeno tudi za obračanje predmeta. Potem je jasno, da je treba za dosego rotacijskega učinka uporabiti na določeni razdalji od osi vrtenja in njene linije delovanja ne bi smelo iti skozi to osi.

Opredelitev navora

Navor ali trenutek sile, označen kot τ vektorska magnituda, ki je odgovorna za sestavljanje vseh teh dejstev, je opredeljen kot:

τ = r x f

Vektor r Usmerjena je od osi vrtenja do točke uporabe sile in udeležba kota med R in F je pomembna. Zato je velikost navora izražena kot:

Vam lahko služi: Newtonov prvi zakon: formule, poskusi in vaje

τ = r.F.Sen q

Najučinkovitejši navor se zgodi, ko r in F So pravokotne.

Če je zaželeno, da ni rotacij ali teh prehodov s konstantnim kotnim pospeševanjem, je potrebno, da je vsota navora, ki delujejo na objekt, nična, analogen tistemu, kar je bilo obravnavano za sile:

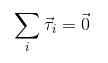
Ravnotežni pogoji

Ravnovesje pomeni stabilnost, harmonijo in ravnotežje. Za gibanje predmeta, ki ima te značilnosti, je treba uporabiti pogoje, opisane v prejšnjih razdelkih:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

Prvi pogoj zagotavlja translacijsko ravnovesje, drugi pa rotacijski. Oba je treba izpolniti, če želi predmet ostati v statično ravnovesje (odsotnost kakršnega koli gibanja).

Prijave

Ravnotežni pogoji so uporabni za številne strukture, saj se pri gradnji stavb ali raznolikih predmetov izdelamo z namenom, da se njihovi deli vzdržujejo v istih relativnih položajih drug z drugim. Z drugimi besedami, da predmet ni razorožen.

To je pomembno na primer pri gradnji mostov, ki ostanejo čvrsti pod nogami, ali pri oblikovanju bivalnih struktur, ki ne spreminjajo položaja ali imajo nagnjenost k odlaganju.

Medtem ko se verjame, da je enotno pravokotno gibanje izjemno poenostavitev gibanja, ki se običajno pojavi malo v naravi, je treba zapomniti, da je hitrost svetlobe v praznini konstantna, in tudi zvok v zraku, če, če meni, da je okolje homogen.

V mnogih mobilnih strukturah, ki jih je ustvaril človek, je pomembno, da se vzdržuje stalna hitrost: na primer na mehanskih stopnicah in montažnih linijah.

Lahko vam služi: drugi zakon termodinamike: formule, enačbe, primeri

Primeri translacijske ravnotežja

To je klasična vaja napetosti, ki držijo svetilko v ravnovesju. Znano je, da svetilka tehta 15 kg. Poiščite veličine potrebnih napetosti, da jih ohranite v tem položaju.

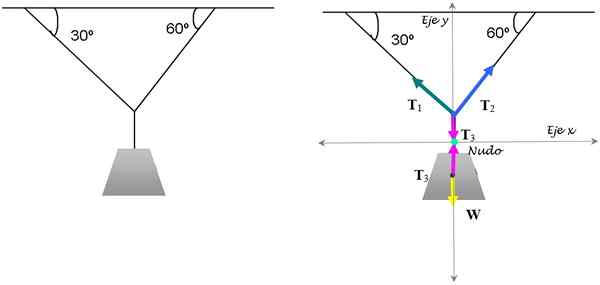Slika 3. Stanje svetilke je zagotovljeno z uporabo stanja translacijskega stanja. Vir: Self Made.

Rešitev

Da bi ga rešili, se osredotočimo na vozel, kjer se tri strune združijo. Ustrezni diagrami prostih telesa za vozel in svetilko so prikazani na zgornji sliki.

Teža svetilke je W = 5 kg . 9.8 m/s² = 49 n. Da je svetilka v ravnovesju, je dovolj, da je izpolnjeno stanje prvega ravnotežja:

T₃ - W = 0

T₃ = W = 49 n.

Napetosti T₁ in T₂ Se morajo razgraditi:

T_1y + T_{2 in} - T₃ = 0 (Poletje sil vzdolž osi y))

-T_1x +T_2x = 0 (Poletje sil vzdolž osi x)

Uporaba trigonometrije:

T₁.Cos 60 ° +t₂ .Cos 30 ° = 49

- T₁.Sen60º +t₂.Sen30º = 0

Gre za sistem dveh enačb z dvema neznankama, katerih odgovor je: T₁ = 24.5 n in T₂ = 42.4 n.

Reference

1. Rex, a. 2011. Osnove fizike. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Ed. Cengage učenje. 120 - 124.
3. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Ed. Cengage učenje. 99-112.
4. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Fizika. Addison Wesley. 332 -346.