Prevod pogojev, primeri, vaje

Navedeno je, da je predmet v Prevodno ravnovesje Ko je vsota sil, ki delujejo nanj. To ne pomeni, da je ostalo nujno, vendar bi bilo gibanje, če bi bilo obstoječe, enotno ali izključno rotacijsko pravokotno, v primeru obsežnega predmeta.

Mehanski ravnotežni pogoji temeljijo na Newtonovih zakonih o mehaniki. Dejansko nam prvi zakon pove, da je predmet v mirovanju ali premika z enotnim pravokotnim gibanjem MRU, pod pogojem.

Ta svetilka je v prevajalskem ravnovesju

Zdaj je posledična neto sila ali sila preprosto vektorska vsota vseh sil, ki delujejo na objekt. Po Newtonovem drugem zakonu mora biti ta vsota enaka izdelku med maso in pospeševanjem, če pa se predmet ne pospeši, se ta vsota razveljavi.

In ker ni pospeška, sta omenjeni dve možnosti: telo je v mirovanju, torej se ne premika ali če je, mora biti z MRU. V prvem primeru govori o statičnem nadnacionalnem ravnovesju, v drugem pa dinamični.

Prevajanje prevoda je pomemben dejavnik v mnogih vidikih inženiringa, na primer v gradbeništvu. Elementi, ki sestavljajo stavbo: tramovi, kabli, okvirji in drugo, morajo biti v ravnovesju, da bi zagotovili stabilnost ograjenega prostora.

Prevajanje ravnotežja se išče tudi v mobilnih strukturah, kot so mehanske stopnice, prometni pasovi in ​​v praksi številnih športov.

[TOC]

Prevod stanje ravnotežja

Recimo, da več sil deluje na telo, ki ga označujemo kot F₁, F₂, F₃.. . F_n, Uporaba krepke črke za poudarjanje dejstva, da so sile vektorji in jih je treba dodati kot take.

Vektorska vsota vseh teh sil se imenuje posledična sila tudi Neto sila. Če ta povzetek povzroči ničelni vektor, je izpolnjen pogoj za prevod:

Vam lahko služi: zaprto električno vezje

F₁+ F₂+ F₃.. .+ F_n = 0

Ta pogoj je mogoče kompaktno zapisati s seštevanjem:

∑ F_Yo = 0

Glede na komponente nastale sile lahko prejšnjo enačbo, ki je vektor, razčleniti na tri skalarne enačbe, po eno za vsako komponento nastale sile:

∑ f_Ix = 0; ∑ f_in = 0 in ∑ f_z = 0

V praksi ni enostavno.

To je razlog, da resnični predmeti skoraj nikoli niso izvzeti iz zunanjih sil, zato je težko pridobiti ravnovesje prevajanja.

Tako inženirji uporabljajo mehanizme za zmanjšanje drgnjenja, kot so ležaji in uporaba mazivnih olj.

Brezplačni diagrami telesa

Diagram prostega telesa je shema, v kateri so sile, ki delujejo na telo. Ko se zahteva prevod prevoda, morajo biti te sile uravnotežene. Na primer, če igrate navpično silo, usmerjeno navzdol, na primer teža, potem mora biti navpična sila, ki ima popolnoma enako velikost.

To silo lahko dobavi z roko, ki zdrži predmet, tako da ne pade, vrvi ali preprosto površine mize.

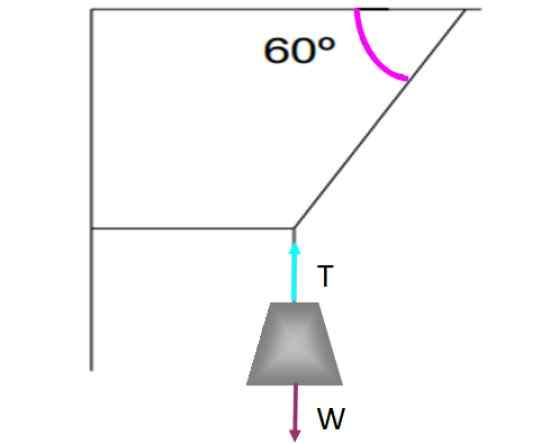
Če je na površini tangencialna sila, na primer kinetično ali statično trenje, mora obstajati še ena nasprotna sila, tako da ravnovesje obstaja. Na primer, opazujmo težo, ki visi iz strun, prikazanih na naslednji sliki.

Primer predmeta, ki je v ravnovesju prevajanja, je to tehtanje, ki je podvržena strehi s pomočjo strun, razporejenih, kot je prikazano na sliki. Vir: f. Zapata.

Teža ostaja v ravnovesju v prevodu in brez premikanja, zahvaljujoč navpični vrvi, ki jo drži z izvajanjem napetosti T ki kompenzira težo W. Vsaka sila je bila predstavljena na zahodu skozi puščico, vsake enake velikosti in z isto smerjo, vendar nasprotno smer.

Vam lahko služi: izobarični postopek: formule, enačbe, poskusi, vaje

Ravnotežna sila

Recimo, da niz sil deluje na predmet. To se imenuje a Sistem sil od tega je mogoče najti, kot je razloženo zgoraj: dodajanje vsakega sistema sili vektorsko.

No, s silo nasprotno od tega rezultata se imenuje izravnalna sila. Če je nastala sila F_R In uravnoteženje je In, tako:

In + F_R = 0

Zato:

In = - F_R

Primeri prevajanja ravnotežja

Številni predmeti, ki jih najdemo vsak dan, znotraj in zunaj doma, so v prevodnem ravnovesju:

Stavbe in ceste

Stavbe in ceste so zgrajene tako, da ostanejo stabilne in se ne obračajo ali propadajo. Vendar pa je v nebotičnikih in na splošno zelo visoki zgradbi potrebna nekaj prožnosti, da se upirajo vetru.

Knjige in predmeti na policah

Knjige v knjižnici in izdelki v trgovinah so predmeti, ki ostanejo v prevodnem ravnovesju in brez premikanja.

Pohištvo

Pohištvo, televizor z ravnim zaslonom in slike na steni, pa tudi svetilke, ki visijo s stropa, če omenimo nekatere predmete, so v prevodu.

Semafor

Semaforji so pritrjeni s objavami in kabli, tako da ne padejo. Vendar vemo, da jih veter niha.

Javna razsvetljava

Javne osvetlitvene luči so tudi v prevodnem ravnovesju, pritrjene na svetlobnih objavah, kot je glavna slika glavne slike.

Vaja rešena

Kakšno velikost naj ima moč F_s statično trenje za škatlo na sliki ostane v mirovanju na sredini nagnjene ravnine kot kot α 37 °? Masa škatle je m = 8 kg.

Vam lahko služi: Gravitacija API: lestvica in klasifikacija surove nafte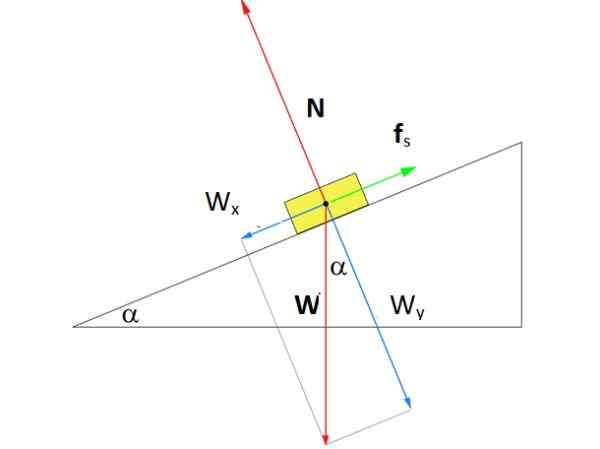Brezplačni karoserijski diagram za objekt za počitek na nagnjeni ravnini. Vir: f. Zapata.

Rešitev

Slika prikazuje diagram prostega telesa na ravnini. Nanjo delujejo tri sile: teža W, usmerjeno navpično navzdol, normalno N, ki je pravokotna sila, ki jo ima površina ravnine nad škatlo, in na koncu statično trenje F_s ki nasprotuje škatli, da zdrsne navzdol.

Pogoj prevoda ravnotežja določa, da:

W + N + F_s = 0

Morate pa se spomniti, da je to vektorska vsota in da jo izvedemo.

Na sliki je bil narisan koordinatni sistem, v katerem se osi X poteka vzporedno s površino nagnjene ravnine. S to izbiro statično trenje pade na tej osi, medtem ko je normalno na osi in. Teža je edina sila, ki je nagnjena in moramo s pomočjo trigonometrije razgraditi:

W_x = W. greh α
W_in = W. cos α

Vsota sil na vsaki osi je:

∑ f_in = N - w_in = 0
∑ f_x = f_s - W_x = 0

Iz te zadnje enačbe sledi:

F_s = W_x

In kot w_x = W. sin α in velikost teže je w = m.G, ki je G vrednost gravitacije, zato je velikost statičnega dotika preprosto:

F_s = m⋅G⋅sen α = 8 kg × 9.8 m/s² × Sen 37 ° = 47.2 n.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 2. Dinamično. Uredil Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Ed. Cengage učenje.
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.