Koncept in primeri nestabilnega ravnovesja

V mehaniki je predmet v Nestabilno ravnovesje Ko ga s silo premika samo iz svojega položaja, se ne vrne vanj. Na primer, kroglica naslednje slike, ko je nad nasipom, je v nestabilnem ravnovesju, ker se bo najmanjša motnja postavila na glavo, brez možnosti, da se vrne s svojimi sredstvi.

Slika 1. Žoga je v nestabilnem ravnovesju v položaju leve, v ravnodušnem ravnovesju v središču in v stabilnem ravnovesju na desni. Vir: Wikimedia Commons.

Po drugi strani pa je, ko je kroglica na ravni površini, kot v položaju središča, govorila, da je v brezbrižno ravnovesje ali nevtralno. Sila, ki jo moti, ga lahko nanesete, premaknete na drugo stran, če pa sila izgine, bo žoga spet stabilna.

Končno je na desni žoga na dnu konkavne sklede. Tudi ta položaj je uravnotežen, vendar stabilno ravnovesje. Sila, ki moti žogo, jo bo le nekoliko nihala okoli prvotnega položaja, da se nanjo vrne k njej.

[TOC]

Vzroki izgube ravnotežja

Skupni predmeti (in ljudje in živali) izgubijo ravnovesje in padejo zaradi navora, ki izvira s težo, silo, ki jo je zemlja izvajala nad vsemi predmeti blizu njegove površine. Ko imate podaljšano telo, se imenuje točka, kjer se imenuje teže Gravitacijski center.

Teža je mogoče uravnotežiti zahvaljujoč podpori, kot je tisto, ki zagotavlja površino, in na ta način se objekt ne bo premaknil. A še vedno se lahko obrne v zvezi z neki točki, saj v razširjenih predmetih ravnovesje sil ni edini dejavnik, ki jih ohranjajo še vedno, ampak tudi kraj, kjer se te sile uporabljajo.

Spodaj je številka z uravnoteženim svinčnikom na konici, v nestabilnem ravnovesju. Vsak zračni tok se bo izkazal, medtem pa se kompenzirata običajna teža in sila, ki se podpira. Poleg tega imata obe sili enako delovno linijo in to poteka skozi vrh svinčnika, kar zagotavlja ravnovesje.

Vam lahko služi: ne -koplanarni vektorji: definicija, pogoji, vaje

Če pa se svinčnik nagiba le malo, kot je prikazano na desni, se linija delovanja teže ustavi skozi konico, ki deluje kot vrtenje. Potem teža povzroči neuravnotežen navor in svinčnik se vrti v smeri rok ure.

Slika 2. Svinčnik, podprt na njegovem konici, je v nestabilnem ravnovesju, majhna motnja bo povzročila, da teža povzroči navor glede na konico in svinčnik bo padel. Vir: f. Zapata.

Dejavniki, ki zagotavljajo stabilnost

Skoraj vedno tisto, kar iščemo, je stabilno ravnovesje, saj je nestabilno ravnovesje, kot že ime pove, precej negotovo. Nadaljuje s primerom svinčnika, ko pade in ostane vodoravno na površini, je nov položaj veliko bolj stabilen kot takrat, ko je bil ustavljen na konici.

To je zato, ker je na eni strani težišče bližje površini, na drugi pa je podporna površina svinčnika veliko večja.

Ko je podporna površina LAR. In če je razdalja od središča gravitacije do površine nižja, je ročica ročice manjša, zato je tudi navor tudi.

Za zaključek, večja kot je osnova za podporo predmeta in bližje njenemu težišču do tal, manj je verjetnost prevračanja in ravnovesje je stabilna. Dojenčki to vedo in zato običajno najprej pokvarijo, preden tvegajo, da stojijo.

In če je telo namesto podprt, je telo suspendirano s točke, ima tudi lokacija težišča vidno vlogo pri vzpostavljanju ravnotežja, kot bo razvidno v naslednjih primerih.

Vam lahko postreže: Mount Olympus (Mars)

Primeri ravnotežja

Ravnotežje v podprtih telesih

Ravnotežje v podprtih telesih je odvisno od:

-Kako blizu težišče površine.

-Velikost osnove predmeta.

Razmislite o stožcu na ravni mizi. Najbolj stabilen položaj brez dvoma je z osnovo stožca, ki je v celoti podprt na mizi. To je stabilen ravnotežni položaj, saj je težišče stožca na osi simetrije in bližje njegovi bazi kot na konico.

Ravno ravnovesje dosežemo tako, da stožec položi in nestabilno ravnovesje ustreza stožcu na njegovem konici, kot je svinčnik, kar morda ni lahka naloga, glede na to, da najmanjše gibanje stožec obrne.

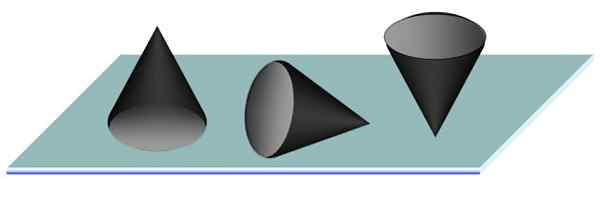Slika 3. Stabilno, ravnodušno in nestabilno ravnovesje stožca, podprtega na mizi. Vir: f. Zapata.

Ravnotežje v suspendiranih telesih

Običajno je najti suspendirana telesa, ki visijo vsaj eno točko, na primer slike in svetilke. Pri vzpostavljanju ravnotežja je treba razmisliti o lokaciji težišča in točke vzmetenja.

Situacijo je enostavno vizualizirati s pomočjo pravokotnega kartonskega lista ali homogenega pravila materiala. Tukaj težišče sovpada z geometrijskim središčem slike, da predpostavljamo, da je masa predmeta enakomerno razporejena.

Za postavitev lista v nestabilno ravnovesje je suspendiran iz točke, ki jo najdemo Spodaj S središča težišča celo drži list med prsti, ne da bi se preveč zategnil, da bi mu pustil svobodo gibanja.

Majhna sila je dovolj, da se list nemudoma vrti v takšnem ali drugačnem smislu. Razlog za zavoj je enak kot v primeru podprtega predmeta: teža izvaja brezkomprodusiran navor, ki olajša vrtenje telesa.

Lahko vam služi: Rešitev toplote: kako se izračuna, aplikacije in vaje

Ko se obračate, list prehaja skozi položaj, ki je stabilnega ravnovesja, v katerem ostane točka vzmetenja od zgoraj od središča teže. Okoli tega položaja se nekoliko giblje in se končno ustavi.

Če se sila ponovno nanese, se lamina spet giblje, vendar se spet vrne v ta položaj, v katerem sta točka vzmetenja in težišče poravnana z navpično.

Končno se ravnodušno ravnovesje preveri tako, da zatič prenesemo natančno skozi težišče. Če je list obrnjen, da ostane v različnih položajih, je razvidno, da med njimi ne bo večje razlike.

Za zaključek je za trupla, suspendirana v nestabilnem ravnovesju, vzmetena točka pod središčem gravitacije. In nasprotno za stabilno ravnovesje.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
3. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5. Ed. Pearson.
4. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
5. Rex, a. 2011. Osnove fizike. Pearson.
6. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.