Mehanske energijske formule, koncept, vrste, primeri, vaje

The Mehanska energija predmeta ali sistema je opredeljen kot vsota njegove potencialne energije in njegove kinetične energije. Kot že ime pove, sistem pridobi mehansko energijo zahvaljujoč delovanju mehanskih sil, kot sta teža in elastična sila.

Glede na količino mehanske energije, ki jo ima telo, bo lahko tudi opravljal mehansko delo.

Slika 1. Gibanje avtomobilov z valjskim gorskim avtomobilom je mogoče opisati z ohranjanjem mehanske energije. Vir: Pixabay.

Energija - vrsta, ki je - je skalarna količina, zato primanjkuje smeri in pomena. Biti In_m Mehanska energija predmeta, Ali njegova potencialna energija in K Njegova kinetična energija, formula za izračun je:

In_m = K + U

Vsaka enota v mednarodnem energetskem sistemu je Joule, ki je skrajšana kot J. 1 j je enakovreden 1 n.m (Newton na meter).

Kar zadeva kinetično energijo, se izračuna na naslednji način:

K = ½ m.v²

Kje m Je masa predmeta in v Njegova hitrost. Kinetična energija je vedno pozitivna količina, saj sta masa in kvadrat hitrosti. Kar zadeva potencialno energijo, če gre za gravitacijsko potencialno energijo, imate:

U = m.g.h

Tukaj m Še vedno je testo, g Je pospešek gravitacije in h To je višina glede na referenčno raven ali če je prednostna, tla.

Če ima zadevno telo elastično potencialno energijo -bi lahko bila vzmet -to je zato, ker je stisnjen ali morda podolgovat. V tem primeru je povezana potencialna energija:

U = ½ kx²

Z k kot vzmetna konstanta, ki kaže, kako enostavno ali težko jo je deformirati in x Dolžina omenjene deformacije.

[TOC]

Koncept in značilnosti mehanske energije

Poglobitev definicije, ki je bila prej, je mehanska energija odvisna od energije, povezane z gibanjem telesa: kinetična energija, plus prispevek potencialne energije, kar je, kot smo rekli spoštovanje tal ali referenčne ravni.

To ponazorimo s preprostim primerom: predpostavimo, da imate lonec na tleh in v mirovanju. Ker je še vedno, nima kinetične energije in je tudi na tleh, kjer ne more padati; Zato nima gravitacijske potencialne energije in njegova mehanska energija je 0.

Recimo zdaj, ko nekdo postavi lonec tik ob robu strehe ali okna, ob 3.Visok 0 metrov. Za to je morala oseba opraviti delo proti gravitaciji. Lonec ima zdaj gravitacijsko potencialno energijo, lahko pade s te višine in njena mehanska energija ni več praznina.

Slika 2. Pot na vrhu okna ima gravitacijsko potencialno energijo. Vir: Pixabay.

V teh okoliščinah ima lonec In_m = U In ta količina je odvisna od višine in teže lonca, kot je navedeno prej.

Recimo, da lonec pade, ker je bil v negotovem položaju. Ko se njegova hitrost povečuje in s seboj njegova kinetična energija, medtem ko se gravitacijska potencialna energija zmanjšuje, ker izgubi višino. Mehanska energija v vsakem trenutku padca je:

Vam lahko služi: kakšne so izpeljane velikosti?

In_m = U + k = ½ m.v² + m.g.h  

Konzervativne in nekonservativne sile

Ko je lonec na določeni višini, ima gravitacijsko potencialno energijo, ker je kdo plezal, je opravil delo proti gravitaciji. Obseg tega dela je vreden enaka tistim, ki pri loncu naredi gravitacijo odpade Z iste višine, vendar ima nasprotni znak, saj je bil narejen proti njej.

Delo, ki sili, kot sta gravitacija in elastičnost, je odvisno le od začetnega položaja in končnega položaja, ki ga je objekt pridobil. Ne glede na to, da je sledila usmeritev, da bi šla od enega do drugega, so pomembne le same vrednosti. Sile, ki se na ta način obnašajo Konzervativne sile.

In ker so konzervativni, omogočajo, da se delo, ki ga opravijo, shranijo kot potencialno energijo v konfiguraciji predmeta ali sistema. Zato je imel lonec na robu okna ali strehe, ki je imel možnost padca in z njim, da bi razvil gibanje.

Po drugi strani pa obstajajo sile, katerih dela so odvisna od poti, ki ji sledi predmet, od katere delujejo. Trenje pripada tej vrsti sil. Podplate čevljev bodo porabljene več, ko boste z enim krajem na cesto s številnimi krogi, kot ko greste za še enega več neposrednega.

Trenje sile opravijo delo, ki zmanjšuje kinetično energijo teles, ker jih upočasni. In zato se mehanska energija sistemov, v katerih deluje trenje.

Del dela, opravljenega s silo, se na primer izgubi s toploto ali zvokom.

Vrste mehanske energije

Mehanska energija je, kot rečeno, vsota kinetične energije in potencialne energije. Zdaj lahko potencialna energija izhaja iz različnih konzervativnih sil: teža, elastična trdnost in elektrostatična sila.

- Kinetična energija

Kinetična energija je skalarna količina, ki vedno postane gibanje. Kateri koli delček ali premični objekt ima kinetično energijo. Predmet, ki se premika v ravni črti, ima kinetično energijo prevajanja. Enako se zgodi, če se vrti, v tem primeru govori o rotacijski kinetični energiji.

Na primer avtomobil, ki se premika po cesti, ima kinetično energijo. Tudi nogometna žoga med premikanjem po igrišču ali oseba, ki hitro hodi, da pride do pisarne.

- Potencialna energija

Vedno je mogoče povezati skalarno funkcijo, imenovano potencialna energija na konzervativno silo. Odlikovani so:

Gravitacijska potencialna energija

Tistega, ki ga imajo vsi predmeti glede na svojo višino glede na tla ali referenčno raven, ki je bila izbrana kot taka. Kot primer ima nekdo, ki je v mirovanju na terasi 10 -zgornje stavbe, potencialno energijo 0 glede na tla terase, vendar ne glede na ulico, ki je 10 nadstropij spodaj.

Elastična potencialna energija

Običajno je shranjen v predmetih, kot so lige in vzmeti, povezane z deformacijo, ki jo doživljajo pri raztezanju ali stiskanju.

Elektrostatična potencialna energija

Shranjen je v sistemu električnih obremenitev v ravnotežju zaradi elektrostatične interakcije med njimi. Recimo, da obstajata dva električna naboja istega ločenega znaka na majhni razdalji; Ker se električni naboji istega znaka odvrnejo, se pričakuje, da je zunanji agent opravil, da bi jih zbližal.

Vam lahko služi: izmenična tokostna vezja: vrste, aplikacije, primeri

Ko je postavljen, sistem uspe shraniti delo, ki ga je agent storil, da jih je konfiguriral v obliki elektrostatične potencialne energije.

Ohranjanje mehanske energije

Vrnitev v padajoči lonec se gravitacijska potencialna energija, ki jo je imela, ko je bila na robu strehe, spremeni v kinetično gibanje gibanja. To se poveča na račun prvega, vendar vsota obeh ostane konstantna, saj padec lonca aktivira gravitacija, ki je konzervativna sila.

Obstaja izmenjava med eno vrsto energije in drugo, vendar je prvotna količina enaka. Zato je veljavno potrditi, da:

Začetna mehanska energija = končna mehanska energija

In_{Začetni m} = E_{M finale}

Druga možnost:

K_začetno + Ali_začetno = K _finale + Ali_finale

Z drugimi besedami, mehanska energija se ne spreminja in ∆E_m = 0. Simbol "∆" pomeni spreminjanje ali razliko med končnim zneskom in začetnim.

Za pravilno uporabo načela ohranjanja mehanske energije za reševanje problemov je potrebno:

-Uporablja se le, kadar so sile, ki delujejo na sistem, konzervativne (resnost, elastična in elektrostatična). V tem primeru: ∆E_m = 0.

-Študijski sistem mora biti izoliran. Nikakor ni prenosa energije.

-Če se pojavi v težavi, potem ∆E_m ≠ 0. Kljub temu bi lahko problem rešili z iskanjem dela konzervativnih sil, saj je vzrok za zmanjšanje mehanske energije.

Odbitek mehanskega ohranjanja energije

Recimo, da konzervativna sila deluje na sistem, ki opravi delo W. To delo povzroča spremembo kinetične energije:

W = ∆K (Cinetic Work-Energy Teorem)

Pomembno je opozoriti, da je kinetika teorema delovne energije uporabna tudi v primeru nekonzervativnih sil.

Po drugi strani je delo odgovorno tudi za spremembo potencialne energije, v primeru konzervativne sile pa je sprememba potencialne energije opredeljena kot negativna od tega dela:

W = -∆U

Ujemanje teh enačb, saj se oba sklicujeta na delo, opravljeno na predmetu:

∆K = -∆U 

K_F - K_tudi = -(u_F - Ali_tudi)

Naročniki simbolizirajo "končno" in "začetno". Združevanje:

K_F + Ali_F = K_tudi + Ali_tudi                                                    

Primeri mehanske energije

Številni predmeti imajo zapletene gibe, v katerih je zapleteno najti izraze za položaj, hitrost in pospešek kot funkcija časa. V takšnih primerih je uporaba načela mehanske energije učinkovitejši postopek kot poskušati neposredno uporabiti Newtonove zakone.

Poglejmo nekaj primerov, v katerih se ohrani mehanska energija:

-Smučar, ki drsi navzdol po snežnih hribih, pod pogojem, da naj bi bila odsotnost trenja. V tem primeru je teža vzročna sila gibanja po celotni poti.

-Ruski gorski vozički, Je eden najbolj značilnih primerov. Tu je tudi teža, ki opredeljuje gibanje in mehanska energija se ohrani, če ni trenja.

Vam lahko služi: ionizacijska energija

-Preprosto nihalo Sestavljen je iz mase, ki je podvržena neiztegljivi vrvi -ne spremeni dolžine -ki se na kratko loči od navpične in je dovoljena za nihanje. Vemo, da se bo sčasoma ustavila zaradi trenja, toda ko se trenje ne upošteva, se ohrani tudi mehanska energija.

-Blok, ki vpliva na pomlad pritrjen na en konec na steno, vse postavljeno na zelo gladko mizo. Blok stisne vzmet, potuje na določeno razdaljo in se nato izstreli v nasprotno smer, ker se vzmet razteza. Tu blok pridobi svojo potencialno energijo zahvaljujoč delu, ki na njem izvira.

-Pomlad in žoga: Ko je vzmet stisnjena z žogo, to odskoči. To je zato, ker ko se pomlad sprosti, potencialna energija postane kinetična energija v žogi.

-Trampolinski skok: Deluje podobno kot pomlad, elastično promovira osebo, ki skoči nanj. To izkorišča svojo težo med skakanjem, s katerim deformira trampolin, vendar ta, ko se vrne v prvotni položaj, daje impulz skakalcu.

Slika 3. Odskočna deska deluje kot pomlad in promovira ljudi, ki skačejo po njej. Vir: Pixabay.

Rešene vaje

- Vaja 1

Predmet mase M = 1 kg se spusti z rampo z višine 1 m. Če je klančina izjemno gladka, izračunajte hitrost telesa ravno takrat, ko vzmet trči.

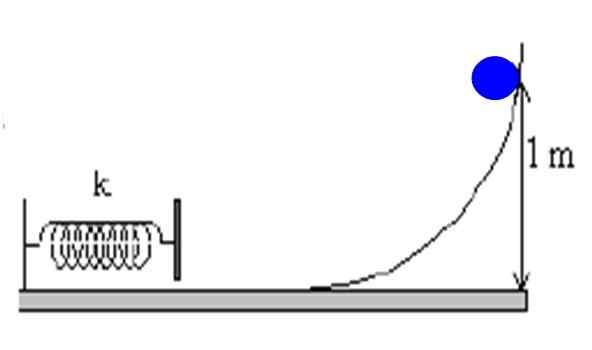Slika 4. Predmet se spusti na klančini brez trenja in stisne vzmet, ki je pritrjena na steno. Vir: f. Zapata.

Rešitev

Izjava poroča, da je rampa gladka, kar pomeni, da je edina sila, ki deluje na telo, njegova teža, konzervativna sila. Tako je navedeno, da uporabimo ohranitev mehanske energije med katerim koli točkami poti.

Razmislite o točkah, označenih na sliki 5: a, b in c.

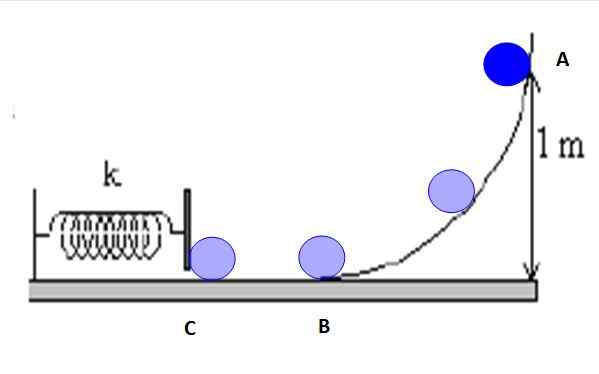Slika 5. Pot, ki sledi predmetu, je trenje in mehanska energija je ohranjena med katerim koli parom točk. Vir: f. Zapata.

Možno je vzpostaviti ohranjanje energije med A in B, B in C ali A in C ali katero koli vmesno točko na klančini. Na primer, med A in C imate:

Mehanska energija pri A = mehanska energija v C

In_ma = E_MC

K_Do + Ali_Do = K_C + Ali_C

½ m.v_Do² + m.g.h_Do = ½ m v_C² + m.g.h_C

Kot je izdano iz točke A, hitrost V_Do = 0, na drugi strani h_C = 0. Poleg tega je masa preklicana, ker je skupni dejavnik. Tako:

g.h_Do = ½ v_C²

v_C²= 2 g.h_Do

- Vaja 2

Poiščite največjo stiskanje, ki ga bo doživela vzmet vaje 1, če je elastična konstanta istega 200 n/m.

Rešitev

Elastična konstanta vzmeti kaže na silo, ki jo je treba uporabiti za deformiranje enote dolžine. Ker je konstanta te pomladi vredna k = 200 n/m, to kaže, da je 200 n potrebno, da jo stisne ali raztegne 1 m.

Biti x Razdalja, ki jo objekt stisne vzmet, preden se ustavi v točki D:

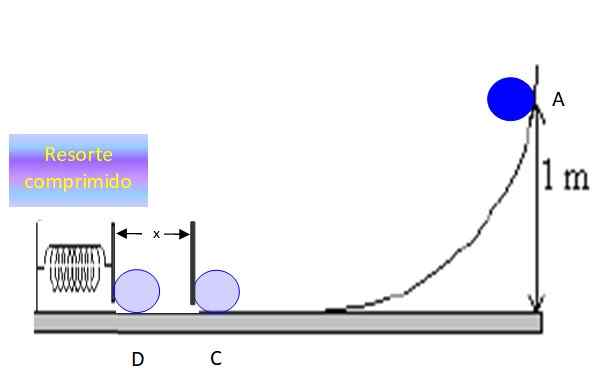Slika 6. Objekt stisne vzmet na x razdaljo in se v trenutku ustavi. Vir: f. Zapata.

Ohranjanje energije med točkami C in D ugotovi, da:

K_C + Ali_C = K_D + Ali_D

V točki C nima gravitacijske potencialne energije, saj je njegova višina 0, vendar ima kinetično energijo. V D se je popolnoma ustavil, zato je tam k_D = 0, namesto tega pa imate na razpolago potencialno energijo stisnjene vzmeti u_D.

Ohranjanje mehanske energije ostaja:

K_C = U_D

½ mV_C² = ½ kx²

 

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
3. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
5. Wikipedija. Mehanska energija.Okrevano od: je.Wikipedija.org.