Helmholtz brez energetskih enot, kako se izračuna, rešene vaje

The Helmholtz brezplačna energija To je termodinamični potencial, ki meri koristno delo zaprtega sistema v pogojih s konstantno temperaturo in prostornino. Helmholtzova prosta energija je označena kot F In je opredeljen kot razlika od notranje energije Ali manj temperaturni izdelek T Za entropijo S:

F = u - t⋅s

Ker je energija, se meri v Joulesu v mednarodnem sistemu (SI), čeprav so lahko tudi druge ustrezne enote ergios (CG), kalorije ali elektronski volti (EV).

Slika 1. Opredelitev Helmholtzove energije. Vir: Pixabay.

Negativna sprememba Helmholtzove energije med postopkom je enaka z največjim delom, ki ga sistem lahko izvede v izokoričnem procesu, torej do konstantne prostornine. Kadar količina ni konstantna, lahko del tega dela opravite na okolju.

V tem primeru se sklicujemo na delo, v katerem se prostornina ne razlikuje, na primer električno delo: dw = φdq, z φ kot električni potencial in q kot električni naboj.

Če je temperatura tudi konstantna, se Helmholtzova energija zmanjša, ko dosežete ravnotežje. Zaradi vsega tega je Helmholtzova energija še posebej uporabna v konstantnih volumskih procesih. V tem primeru imate:

- Za spontani postopek: ΔF < 0

- Ko je sistem v ravnovesju: Δf = 0

- V ne-spontanem procesu: Δf> 0.

[TOC]

Kako se izračuna brezplačna energija Helmholtz?

Kot je navedeno na začetku, je Helmholtzova energija opredeljena kot "notranja energija ali sistem, razen produkta sistema absolutne temperature T s entropijo sistema":

F = u - t⋅s

Je funkcija temperature T in volumna V. Koraki za vizualizacijo tega so naslednje:

Vam lahko služi: notranji elektroni

- Začenši od prvega zakona termodinamike, notranje energije ali je povezan z entropijo S sistema in njegovim zvezkom V za reverzibilne procese z naslednjim diferencialnim odnosom:

du = dq - dw = tds - pdv

To sledi, da je notranja energija ali je funkcija spremenljivk S in V, Zato:

U = u (s, v)

- Zdaj definicija F In izhaja:

df = du - d (ts) = du - tds - sdt

- Zamenjava diferencialnega izraza, pridobljenega za DU v prvem koraku, ostaja:

DF = TDS - PDV - TDS - SDT = -SDT - PDV

- Končno je sklenjeno, da je F funkcija temperature T in volumna V in se lahko izrazi kot:

F = f (t, v)

Slika 2. Hermann von Helmholtz (1821-1894), nemški fizik in zdravnik, je bil priznan za svoj prispevek k elektromagnetizmu in termodinamiki, med drugimi področji znanosti. Vir: Wikimedia Commons.

Spontani procesi

Helmholtzova energija je mogoče uporabiti kot splošno merilo spontanosti v izoliranih sistemih, vendar preden je treba določiti nekatere koncepte:

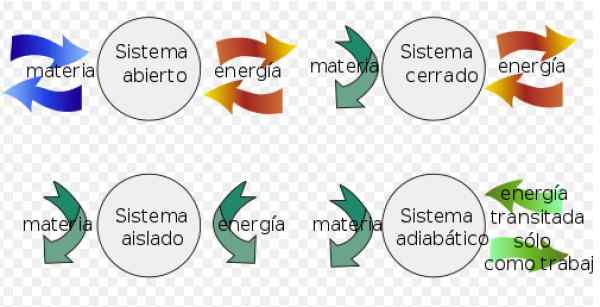
- A sistem zaprt Lahko izmenja energijo z okoljem, vendar ne more zamenjati snovi.

- Namesto a izolirani sistem ne izmenjuje snovi ali energije z okoljem.

- Končno a odprt sistem izmenjava snovi in ​​energije z okoljem. 

Slika 3. Termodinamični sistemi. Vir: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // creativeCommons.Org/licence/by-sa/4.0)].

V reverzibilnih procesih se sprememba notranje energije izračuna na naslednji način:

DU = TDS - PDV

Zdaj predpostavimo, da je konstanten volumen (izokorični) postopek, v katerem ima drugi izraz prejšnjega izraza ničelni prispevek. Prav tako se je treba spomniti, da po besedah Neenakost Clausius: 

ds ≥ dq/t

Takšna neenakost velja za izoliran termodinamični sistem.

Tako da je za postopek (reverzibilno ali ne), v katerem se ohrani konstanta, izpolnjen:

Vam lahko služi: fosforna kislina (H3PO4)

T ds ≥ du (Pri fiksni glasnosti)

Ob upoštevanju tega:

df = du - t ds 

Izpolnjeni bomo morali v izokoričnem procesu pri konstantni temperaturi, ki: DF ≤ 0, kot je navedeno na začetku.

Tako, da je energija Helmholtz F v spontanem procesu padajoča količina, medtem ko je izoliran sistem. F doseže svojo minimalno in stabilno vrednost, ko je doseženo reverzibilno ravnovesje.

Rešene vaje

Vaja 1

Izračunajte variacijo proste energije Helmholtz F za 2 mola idealnega plina pri temperaturi 300K med izotermalno širitvijo, ki vodi v sistem začetne prostornine 20 litrov do končne prostornine 40 litrov.

Rešitev

Začenši iz definicije F:

F = u - t s

Potem bo končna variacija F, imenovana ΔF,:

Δf = ΔU - t ΔS

Ker izjava navaja, da je temperatura konstantna: ΔT = 0. Vendar je v idealnih plinih notranja energija odvisna le od njegove absolutne temperature, a ker gre za izotermalni postopek ΔU = 0 in Δf = - t ΔS. Za idealne pline je napisana entropijska variacija izotermalnega procesa tako: 

ΔS = n.R.ln (v₂/V₁)

Uporaba tega izraza:

ΔS = 2 mola x 8,314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Končno je sprememba v Helmholtzovi energiji:

Δf = - t ΔS = - 300K x 11,53 j/k = -3457,70 J.

Vaja 2

Znotraj cilindra je bat, ki ga deli na dva odseka in na vsaki strani bata sta n moli idealnega monoatomskega plina, kot je prikazano na spodnji sliki.

Stene jeklenk so dobri toplotni vodniki (diatermični) in so v stiku s rezervoarjem temperature T_tudi.

Začetna prostornina vsakega od cilinderskih odsekov je V_1i in v_2i, Medtem ko so njegovi končni zvezki V_1f in v_2F Po navideznem premiku. Bat se premika s batom, ki hermetično prečka dva tapasa cilindra.

Lahko vam služi: Tecnecio (TC): struktura, lastnosti, uporabe, pridobivanje

Prosimo, da najde:

a) Sprememba notranje energije plina in delo, ki ga opravlja sistem in

b) Helmholtzova sprememba energije.

Rešitev

Ko se bat premika kvaziestatično, mora zunanja sila, nanesena na bat.

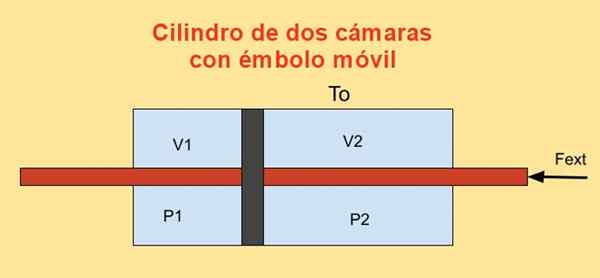Slika 4. Sprememba proste energije F v jeklenki z dvema kamerama. Vir: f. Zapata.

Delovno mesto Dw Izdelala zunanja sila F_ext Med neskončnomaškim premikom Dx je:

Dw = - f_ext Dx = (str₁ - Str₂) A dx = p₁ DV₁ + Str₂ DV₂

Kjer je bil uporabljen odnos DV₁ = - DV₂ = DX, biti do Območje bata. Po drugi strani je sprememba energije Helmholtza: 

Df = -sdt - pdv

Ker se med postopkom temperatura ne spreminja, potem dt = 0 in Df = - pdv. Uporaba tega izraza na vsakem odseku jeklenke imate:

dw = str₁ DV₁ + Str₂ DV₂ = - df₁ - Df₂

Biti F₁  in F₂ Helmholtzove energije v vsaki od kamere.

Končno w delo je mogoče izračunati iz končne variacije Helmholtzove energije vsake kamere:

W = -Δf₁ - Δf₂

Rešitev b

Za iskanje spremembe energije iz Helmholtza se uporablja definicija: F = u - t s. Kot v vsaki kameri imate idealen monoatomski plin pri konstantni temperaturi T_tudi, Notranja energija se ne spreminja (ΔU = 0), tako da: Δf = - t_tudi ΔS. Poleg:

ΔS = nr ln (v_F/Videl)

Da z zamenjavo končno omogoča opravljeno delo, je: 

W = -t_tudi Nr ln (v_1f /V_1i) -TO NR Ln (V_2F /V_2i) = -Δf₁ -Δf₂

W = - do nr ln [(v_1f ⋅ v_1i)/(V_{2F .}V_2i) = - Δf_skupaj

Biti Δf_skupaj Skupna sprememba Helmholtzove energije.

Reference

1. Castaños e. Proste energijske vaje. Okrevano od: lidiaconlachimica.WordPress.com
2. Librettexts. Helmholtz Energy. Okrevano od: kem.Librettexts.org
3. Librettexts. Kaj je brezplačna energija. Okrevano od: kem.Librettexts.org
4. Wikipedija. Helmholtz Energy. Okrevano od: je.Wikipedija.com
5. Wikipedija. Helmholtz brezplačna energija. Pridobljeno iz: v.Wikipedija.com