Clausius-Clapeyronova enačba, za kaj gre, primeri, vaje
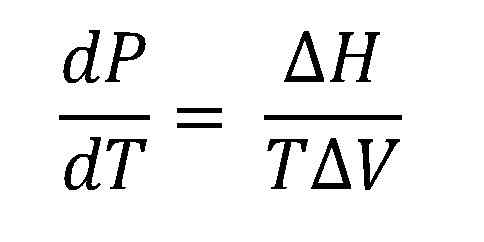
- 768
- 181
- Ricky Dach
The Clausius-Clapeyronova enačba To je ena, ki povezuje spremembe parnega tlaka in temperature, v fazi ali spremembi prehoda v stanju. Uporablja se za sublimacije, izhlapevanje, združitve ali celo pri spremembah v kristalnih fazah. Omeniti velja, da ta enačba velja za čisto snov, ki je v ravnovesju.
Ta enačba izhaja iz termodinamičnih zakonov in p-t diagramov za snov, kjer opazimo linijo sobivanja; tisto, ki ločuje dve različni fazi (tekoča vapo, trdno-tekočina itd.). Za prenos te linije je potreben dobiček ali izguba toplote, na primer entalpizacija uparjanja, ΔHVap.
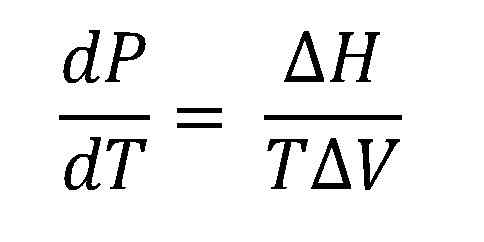 Clausius-Clapeyronova enačba. Vir: Gabriel Bolívar.
Clausius-Clapeyronova enačba. Vir: Gabriel Bolívar. Višja slika prikazuje enačbo Clausius-Clapeyrona, preden je bila integrirana. Običajno se običajno uporablja za sisteme tekočine, kjer se uporablja ΔHVap in želite izračunati, kakšen bo tlak tekoče pare pri določeni temperaturi. Služi tudi za izračun ΔHVap določene tekočine v temperaturnem območju.
Clausisu-Clapeyronova enačba se uporablja tudi precej pogosto za preučevanje sprememb tlaka v hlapnih trdnih snovi; to pomeni, da je sublimacijska entalpija, ΔHsub.
[TOC]
Za kaj je enačba Clausisu-Clapeyron za?
Izračun tlakov in entalpije uparjanja
Iz enačbe Clausius-Clapeyrona od zgoraj so končno izvedeni nekateri matematični premisleki, da končno izvedejo integracijo. Na primer, za sistem s tekočimi hlapi se domneva, da je ΔHVap Ne razlikuje se glede na temperaturo in da ΔV ustreza izključno volumnu pare, ki zaničuje prostornino tekočine (Vpara-Vtekočina = Vpara).
Ob predpostavki, da se Steam obnaša kot idealen plin in integracija, je pridobljena enačba Clausius-Clapeyrona:
Vam lahko služi: hlapnost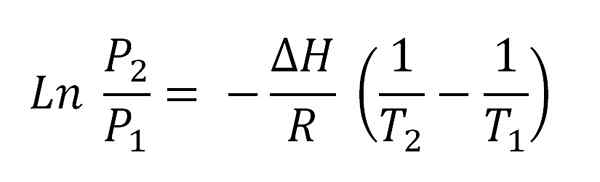 Vgrajena enačba Clausius-Clapeyron.
Vgrajena enačba Clausius-Clapeyron. Ta enačba ustreza enačbi vrstice, ki je grafična kot:
Ln P proti 1/t
In katerih negativni naklon je (ΔH/R). Da bi dosegli to enačbo, mora biti ΔH konstanten v temperaturnem intervalu (t2-T1), v katerih se parni tlaki merijo v ravnovesju s tekočino.
Če se domneva, da se ΔH v majhnih temperaturnih intervalih malo razlikuje, je mogoče uporabiti enačbo te črte za napovedovanje sprememb v parni tlak tekočine; In še več, lahko določite njegov ΔH uparjanja.
Večje kot so upoštevani intervali temperature, največji odstopanje te enačbe eksperimentalnih podatkov in manj bo izpolnjen.
Določitev faznih sprememb
Tako enačba Clausius-Clapeyrona postane razvoj tangentne črte do sobinske črte med dvema fizičnima fazama, kar opazimo v katerem koli diagramu P-T za snov.
Če pride do fazne spremembe, se bo na pobočju spremenila in ΔH ne bo enak. Torej, ko se dokažejo močna odstopanja in enačba ne uspe, je znak, da v intervalu temperature snov doživi drugo fazno spremembo. To pomeni, da preneha biti sistem s tekočino, saj se prenese na linijo sobivanja.
Uporabite primere
- Enačba Clausius-Clapeyron je bila uporabljena v meteorologiji za preučevanje vedenja oblakov, tudi tistih, ki so prisotni na drugih planetih ali lune z atmosferi.
Vam lahko služi: glukonska kislina: struktura, lastnosti, sinteza, uporaba- Uporablja se pri določanju fuzijske entalpije več kovin, kot sta natrij in galij, in za ekstrapolacijo njihovih parnim tlakom pri zelo visokih temperaturah.
- Uporablja se tudi za določitev entalpije izhlapevanja snovi, kot so plinasti klor, ogljikov tetraklorid, tekoča voda, led in jod.
- Služil je tudi za preučevanje faznih sprememb v kristalnih strukturah. V tem zadnjem primeru je integrirana enačba Clausius-Clapeyrona videti izjemno drugačna, saj enaki premisleki, ki se sprejmejo za tekočinski sistem, ni mogoče izdelati za ΔV. Spremembe glasnosti iz ene faze v drugo so tokrat majhne.
Rešene vaje
- Vaja 1
Icenski parni tlak je 4.58 Torr pri 0 ° C in 1.95 Torr A -10 ° C. Kakšna je vaša sublimacijska entalpija v tem temperaturnem območju?
Upoštevajte, da imamo dva tlaka in dve temperaturi:
Str1 = 4.58 Torr
Str2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Temperaturne enote pretvorimo iz ° C v K, ker ima konstanta R plinov K v njenih enotah:
R = 8.314 J/K
Tako uporabljamo integrirano enačbo Clausius-Clapeyrona in jasno ΔHsub, ki bi ostal kot:
ΔHsub = -Rln (str2/P1) / (1 / t2 - 1 /t1)
Če želite več udobja nadomestiti le s številkami, vendar vedoč, da bo končna enota Joule:
ΔHsub = -(8.314) ln (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Ali 51.07 J, če upoštevamo nekaj decimalk. Ta vrednost bo predstavljena nihanja, odvisno od intervalov t2-T1 in nekaterih tlakov pare.
- Vaja 2
Vrelišča etanola pri tlaku 760 Torr (1 atm) je 78.3 ° C in njegova entalpija iz uparjanja je 39.3 kJ. Kakšen bo vaš parni tlak pri temperaturi 46 ° C?
Lahko vam služi: tantalus: struktura, lastnosti, uporabe, pridobivanjeIdentificiramo podatke:
Str1 = 760 Torr
Str2 = ?
T1 = 78.3 ° C + 273 = 351.3 k
T2 = 46 ° C + 273 = 319 K
ΔHVap = 39.3 kJ ali 39300 J
Torej, moramo razčistiti p2 integrirane enačbe Clausius-Clapeyrona. Ponovno bodo enote izpuščene za udobje in izračuni bodo razviti korak za korakom:
Ln (str2/P1) = -(ΔHVap/R) (1/t2 - 1/t1)
Ln (str2/760) = -(39300/8.314) (1/319 - 1/351.3)
Ln (str2/760) = -1.36
Uporaba eksponentne funkcije na obeh straneh enačbe, da bi lahko očistili p2 bomo imeli:
E (ln P2/760) = e(-1.36)
Str2/760 = 0.256
Str2 = 0.256 (760)
= 195 Torr
Pri nižji temperaturi (46 ° C) nižji tlak (195 Torr). Pravzaprav je imel etanol pritisk 760 Torr do 78.3 ° C, govorimo o njegovi običajni vrelišču. To je vedenje, ki se pričakuje za vse tekočine
Na splošno so tovrstne vaje Clausius-Clapeyrona sestavljene iz čiščenja p2, T2 ali ΔH uparjanja ali sublimacije. Izračuni se bistveno spremenijo, kadar je treba upoštevati tudi ΔV, še posebej, če gre za trdne sisteme ali ravnotežje.
Reference
- Whitten, Davis, Peck & Stanley. (2008). Kemija. (8. izd.). Cengage učenje.
- Wikipedija. (2020). Clausius-Clapeyronski odnos. Pridobljeno iz: v.Wikipedija.org
- Državna univerza San José. (s.F.). Enačba Clausius-Clapeyrona:
SPIS izpeljava in uporaba v meteorologiji. Okreval od: sjsu.Edu - Bodner Group. (s.F.). Enačba Clausius-Clapeyrona. Pridobljeno od: chemed.Kem.Purdue.Edu
- Chieh c. & CENSEULO a. (18. maja 2020). Clausius-Clapeyronova enačba. Kemija librettexts. Okrevano od: kem.Librettexts.org
- Walter J. Moore. (1962). Fizikalna kemija. (Četrta izdaja). Longmans.

