Matematika

Diskretne distribucije

Diskretne distribucije
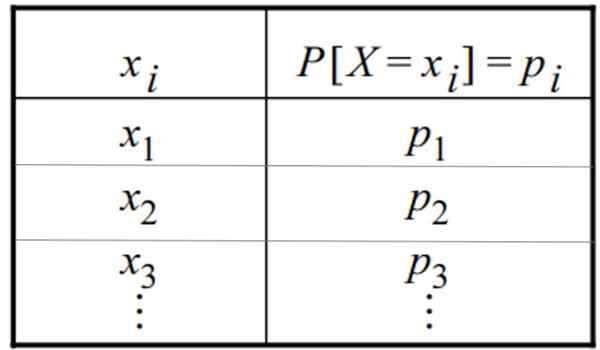Tabela diskretne porazdelitve verjetnosti. Vir: f. Zapata

Kaj je diskretna porazdelitev?

A Diskretna distribucija verjetnosti je funkcija f (xYo), ki dodeli vsaki vrednosti diskretne spremenljivke: x1, x2, x3,... xYo, določen pojav pojavljanja p (x = xYo). Ta funkcija je znana tudi kot "Funkcija verjetnosti mase".

Diskretna porazdelitev verjetnosti je mogoče dati v obliki tabele ali grafike. Tabela ima to splošno obliko, v kateri se spremenljivka pojavi v enem stolpcu, v drugem pa tudi njegove verjetnosti:

Verjetne masne funkcije imajo naslednje splošne značilnosti:

  • Verjetnost strYo katerega koli X dogodkaYo Je med 0 in 1, celo nekatere od teh mejnih vrednosti: 0 ≤ x ≤ 1.
  • P (x = xYo) = pYo Zato vzemite pozitivne vrednosti: p (x = xYo) ≥ 0.
  • Res je, da ∑ p (xYo) = 1 za vse možne vrednosti x.

Porazdelitev verjetnosti opisuje vedenje populacije, ki ga opisujejo njegovi parametri: povprečno μ, varianta σ2 in standardni odklon s = σ σ2.

Nato so na kratko opisane najpomembnejše diskretne distribucije:

Enotna porazdelitev

Je najpreprostejša diskretna porazdelitev vseh. V njej lahko spremenljivka vzame "n" diskretne vrednosti: x1, x2, x3,... xYo, Vse z isto verjetnostjo. V tem primeru je distribucija podana z:

Binomna porazdelitev

Velja za izkušnje z le dvema možnima in medsebojno izključujočima rezultatima, ki se običajno imenujeta "uspeh" in "neuspeh", označena kot E in F. Dejstvo, da se dogodek imenuje "uspeh", ne pomeni nujno, da je to dobra stvar, ampak je poljubno oznako.

Verjetnost uspeha P (e) v "n" vajah je označena kot P, in verjetnost neuspeha p (f), kot je Q = 1 - p.

Če "x" predstavlja določeno število uspehov v "n" neodvisnih preskušanjih, je res, da: 0 ≤ x ≤ n. In verjetnost pojavljanja P (x) dogodka se izračuna z naslednjo formulo:

Lahko vam služi: kvadratni centimetri do kvadratnih metrov (cm² do m²)

Kjer x = 0, 1, 2, 3 ..., n in simbol (!) pomeni "faktorial":

x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1

0! = 1

Poissonova distribucija

V tej porazdelitvi naključna spremenljivka x kaže, kolikokrat se dogodek pojavi v nekem intervalu, ki je lahko časa, razdalje ali drugega. Pojavi dogodka so naključni, neodvisni in se enakomerno porazdelijo skozi zadevni interval.

Ko se ti pogoji, se izračuna verjetnost, ki je odvisna od povprečja μ in števila Eulerja ali števila "E"::

Možnosti dogodkov s to porazdelitvijo so majhne, ​​zato se imenujejo "zakon redkih primerov".

Binomski pristop za porazdelitev

Poissonova porazdelitev služi kot pristop k binomski porazdelitvi, kadar je n velik (n≥ 100) in P je majhen (NP ≤ 10). V tem primeru se povprečni μ izračuna kot:

μ = n ∙ p

Hipergeometrična porazdelitev

Uporablja se, kadar verjetnosti niso neodvisne, torej po izvedbi poskusa pogoji niso več enaki. To se zgodi pri pridobivanju vzorcev brez zamenjave iz populacije, zato binomne porazdelitve ni več mogoče uporabiti.

Če je populacija sestavljena iz dveh vrst predmetov, ki se razlikujejo od in B, pri naključnih predmetih in brez zamenjave, je verjetnost pridobivanja X predmetov tipa A:

Kjer sta A in B ustrezna količina predmetov vsake vrste, prisotna v populaciji.

Če pa je populacija zelo velika, tudi če ni zamenjave, je težko izbrati isti element, tako.

Vam lahko služi: kocka razlika: formule, enačbe, primeri, vaje

Primeri

Kovanci se lansirajo

CO -LACKES so zelo ilustrativni primeri:

-Začetek poštene valute in dobite obraz. Znano je, da ima 1 obraz ½ verjetnosti odhoda in križ (0 obraza), enako. Porazdelitev je prikazana v tej tabeli:

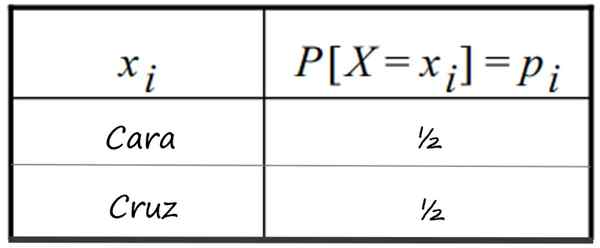Tabela diskretne verjetnosti, ki sledi uvedbi 1 poštene valute. Vir: f. Zapata

-Hkratni posnetek dva Iskreni kovanci in možne številke obrazov, ki jih je mogoče dobiti.

Diskretna tabela za distribucijo verjetnosti, ki sledi uvedbi dveh poštenih valut, z namenom pridobivanja katerega koli obraza ali ne. Vir: f. Zapata

Spremenljivke z enakomerno porazdelitvijo

-Izbor celoštevilčne številke, ki je enakomerna ali nenavadna: vsaka je verjetnost, enaka ½ izbrane v naboru celotnih številk.

-Začetek poštene kocke. V tem primeru je 6 oštevilčenih obrazov in vsaka ima enako verjetnost za odhod: 1/6.

-Izbor teme za opravljanje izpita, izbran med n vprašanji, če so vsi enako verjetni.

Spremenljivke z binomno porazdelitvijo

-Število obrazov, ki se pojavijo z lansiranjem poštenega kovanca.

-Od populacije 250 družin je število teh, ki imajo 2 otroka.

-Količina palic, ki preživijo, po vrtnarju 20 Rosales na vrtu.

-Od študije s 50 bolniki, število, ki je predstavljalo negativno reakcijo na zdravilo.

-Število študentov, odobrenih na izpitu verjetnosti, skupine, ki jih sestavlja 100 študentov.

Spremenljivke s Poissonovo distribucijo

-Število klicev na minuto Klicni center Podjetja.

-Število velikih potresov na leto za določeno geografsko območje.

-Število tornadov, ki so v zadnjem letu prizadeli določeno regijo.

-Število dreves, okuženih z glivico, na kvadratni hektar gozda.

Spremenljivke s hipergeometrično porazdelitvijo

-Uspehi številk ali zmagovalne kombinacije pri igrah na srečo.

Vam lahko služi: sočasni vektorji: značilnosti, primeri in vaje

-Izbira določenega števila samic ali samcev v vzorcu n rib rib.

Rešene vaje

Vaja 1

Študija je ugotovila, da jih naključno izbrani odrasli, ki imajo pametne telefone, 54% jih uporablja v razredu ali sestankih. Želite najti verjetnost, da jih naključno izbira 8 ljudi s pametnim telefonom, točno 6 pa jih uporablja v razredu ali sestankih.

Rešitev

Ta eksperiment se strinja z binomskim poskusom, saj je rezultat binarni: oseba se po telefonu sprejme v razred ali ga ne vzame ven. Dejstvo, da oseba uporablja telefon v razredu, se lahko imenuje uspeh, in neuspeh, če tega ne stori (preden je bilo razloženo, da je ta izbira popolnoma poljubna).

V tem primeru: p = 0.54 in Q = 1- 0.54 = 0.46.

Ker je 8 ljudi naključno izbranih, je n = 8 in vrednost x 6, zato so na voljo potrebne vrednosti, ki jih nadomeščajo v formuli binomne porazdelitve:

Vaja 2

Za nedavno leto je klinika zabeležila 4221 rojstev. S temi edinstvenimi podatki določite verjetnost, da je v enem dnevu 15 rojstev. Je ta dogodek redki?

Rešitev

Poissonova porazdelitev se uporablja, saj se zahteva, da ugotovi verjetnost pojava dogodka, ki se pojavi v časovnem intervalu. V tem primeru je spremenljivka količina rojstev in interval je 1 dan.

Poissonova distribucijska formula potrebuje povprečno rojstvo na dan, kar je enostavno izračunati:

Zato je verjetnost X = 15 rojstev/dan:

Rezultat je mogoče izraziti v odstotkih za jasnost: 6.42% verjetno, da se vsak dan zgodi natanko 15 rojstev. Dogodek je malo verjeten, čeprav v nobenem primeru nemogoče.