Enotna porazdelitev nadaljuje z značilnostmi, primeri, aplikacijami

Naključna spremenljivka ima a Neprekinjena enotna porazdelitev Če je verjetnost, da vzamemo vrednost, v končnem intervalu [a, b], je enaka za kateri koli pododstavek enake dolžine.

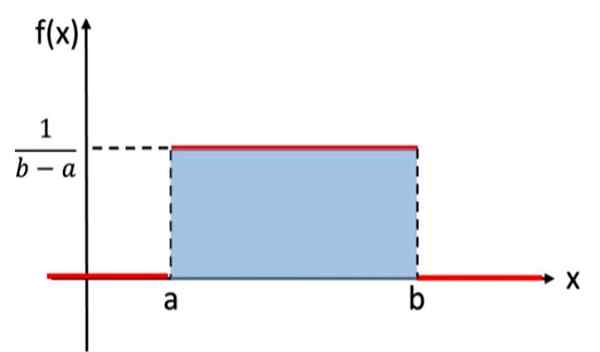
Ta porazdelitev je analogna diskretni enakomerni porazdelitvi, ki je vsakemu rezultatu naključnega poskusa dodelila enako verjetnost, vendar je v tem primeru spremenljivka, ki jo je treba upoštevati. Na primer, eksperiment, ki je sestavljen iz izbire naključnega resničnega števila, med vrednostmi A in B, sledi enakomerni porazdelitvi. Tu imate svoj graf:

Slika 1. Graf funkcije gostote neprekinjene normalizirane enakomerne porazdelitve

V matematični zapisu ima neprekinjena enotna porazdelitev funkcijo gostote, opredeljena kot funkcija na koščke ali po odsekih, ki jih je mogoče zapisati kot:

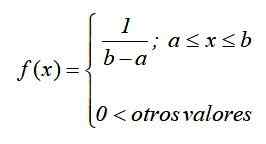
Graf te funkcije, znan kot Funkcija krivulje ali gostote, Je pravokotnik, zato je neprekinjena enotna porazdelitev znana tudi kot Pravokotna porazdelitev In je najpreprostejša od neprekinjenih distribucij.

Območje pod grafom porazdelitve verjetnosti je enako 1 in vedno ima pozitivne vrednosti. Enotna porazdelitev izpolnjuje ta merila. Za preverjanje, ali je območje 1, ni treba neposredno integrirati, saj je območje zasenčenega pravokotnika na sliki 1 izračunati po formuli:

Območje = višina x

Poznavanje območja pod krivuljo gostote je zelo pomembno, saj obstaja povezava med območjem in verjetnostjo pojava dogodka, ki je za to porazdelitev določena v naslednjem razdelku.

Nenehne značilnosti enotne porazdelitve

Za neprekinjeno enotno porazdelitev je značilna:

Funkcija gostote

Naj bo X neprekinjena naključna spremenljivka, ki spada v interval [a, b], nato pa:

Lahko vam služi: linearne transformacije: lastnosti, kakšne so uporaba, tipi, primeri

Funkcija distribucije

S pomočjo porazdelitvene funkcije se izračuna verjetnost, da naključna spremenljivka x vzame vrednost x iz možnih vrednosti intervala [a, b]. Za neprekinjeno porazdelitev se na splošno izračuna na ta način:

V primeru neprekinjene enotne porazdelitve je omenjena verjetnost F (x) enakovredna območju pravokotnika, katerega osnova je (x-a), njegova višina pa (B-A):

Matematično, če f (x) = pr (x = x), se z deli vzpostavi naslednja funkcija, v skladu s prejšnjim rezultatom:

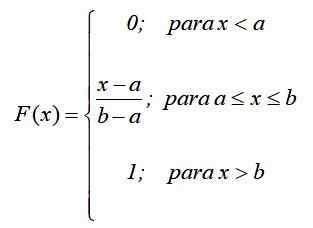
Na ta način je bilo tisto, kar je bilo že rečeno: verjetnost je odvisna le od vrednosti (x-a) in ne od njegove lokacije v intervalu [a, b]. Graf funkcije distribucije je:

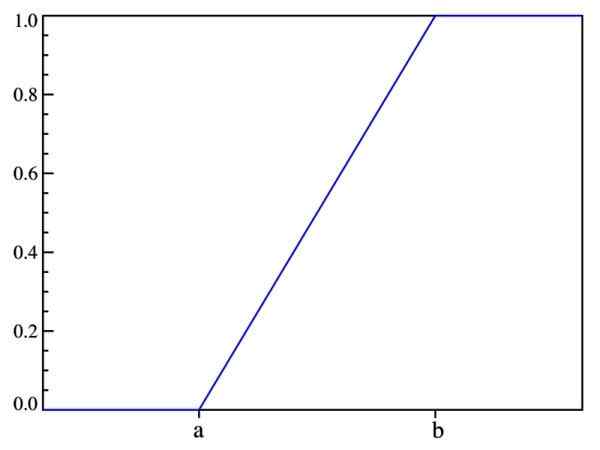Slika 2. Graf funkcije distribucije f (x). Vir: Wikimedia Commons.

Pričakovana vrednost, odstopanje in standardni odklon

Po številnih poskusih z neprekinjeno naključno spremenljivko se imenuje njegova povprečna vrednost pričakovana vrednost, Označen je kot E (x) in se izračuna z naslednjim integralom:

Kar zadeva varianco, je opredeljen z:

V (x) = e (x²) - Ex)²

Zato:

Končno je standardni odklon:

D (x) = √ V (x)

Mediana, moda, simetrija in curtoza 

Lahko je enostavno preveriti, ali je mediana, ki je osrednja vrednost enakomerne porazdelitve, enaka povprečnemu povprečju, in ker ni nobene vrednosti, ki bi se ponavljala več kot drugi, saj so v intervalu enako verjetni [a, b ], moda ne obstaja.

Kar zadeva simetrijo, je enakomerna porazdelitev simetrična in curtoza, ki je stopnja, do katere so vrednosti okoli središča koncentrirane -6/5.

Vam lahko služi: kakšnih je 7 elementov oboda?

Primeri

Različne situacije je mogoče modelirati z neprekinjeno porazdelitvijo in tako napovedati njihovo vedenje. Tu je nekaj primerov:

Primer 1

Podjetje, ki zagotavlja električno storitev, zagotavlja enakomerno porazdeljene napetostne ravni, med 123.0 V in 125.0 V. To pomeni, da je v domačem posnetku mogoče pridobiti katero koli napetost, ki spada v ta interval.

Potem, kot je razvidno zgoraj, je graf funkcije gostote rdeči pravokotnik:

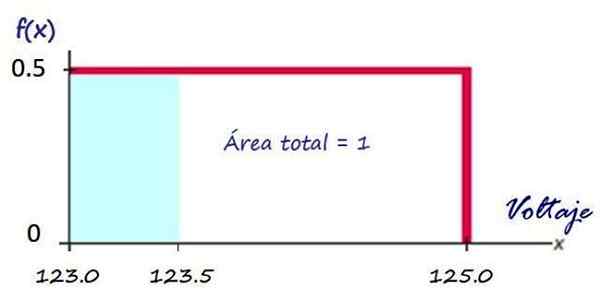Slika 3. Funkcija gostote za napetost, ki jo dostavlja električna družba. Vir: f. Zapata.

Izračun verjetnosti, da boste imeli napetost v danem intervalu, je na primer zelo enostavno, kakšna je verjetnost, da bo podjetje poslalo napetost manj kot 123.5 v?

Ta verjetnost je enakovredna območju zasenčenega pravokotnika v modri barvi:

P (x<123.5) = (123.5 −123.0)x 0.5 = 0.25

In kakšna je verjetnost, da je napetost večja od 124.0 V?

Ker je skupna površina enaka 1, je iskana verjetnost:

P (x> 124.0 V) = 1 - (1 × 0.5) = 0.5

Smiselno, od 124.0 je natančno vrednost v središču intervala.

Primer 2

Določena naključna spremenljivka X ima enakomerno porazdelitev v intervalu [0,100]. Določiti:

a) Verjetnost, da je vrednost x manjša od 22.

b) verjetnost, da X prevzame vrednosti med 20 in 35.

c) pričakovana vrednost, odstopanje in standardni odklon te porazdelitve.

Odgovor na

Določen je podobno kot prejšnji primer, vendar moramo najprej določiti višino pravokotnika, pri čemer ne pozabimo, da mora biti skupna površina enaka 1:

Območje = 100 × višina = 1

Zato ima pravokotnik višino, ki je enaka 1/100 = 0.01

Vam lahko služi: Decagon: redne, nepravilne, lastnosti, primeri

P (x<22) = 22×0.01 = 0.22

Odgovor b

Zahtevana verjetnost je enakovredna območju pravokotnika, katerega širina je (35 - 20) in katerih višina je 0.01:

P (22

Če raje greste neposredno na zgornjo funkcijo distribucije, potem morate samo zamenjati vrednosti v:

P (20≤x≤35) = f (35) -f (20)

Z f (x), ki ga daje:

F (x) = (x-a) / (b-a)

Vrednosti, ki jih je treba uvesti, so:

A = 0

B = 100

F (35) = (35-0) / (100-0) = 0.35

F (20) = (20-0) / (100-0) = 0.dvajset

P (20≤x≤35) = 0.35-0.20 = 0.petnajst

Odgovor c

Pričakovana vrednost je:

E (x) = (a+b)/2 = (100+0)/2 = 50

Varianta je:

V (x) = (b-a)²/12 = (100-0)²/12 = 833.33

In standardni odklon je:

D (x) = √833.33 = 28.87

Prijave

Ta porazdelitev je uporabna, kadar se izvajajo statistični simulacijski procesi ali pri delu na dogodkih, katerih pogostost videza je redna.

Naključne številke

Nekateri programski jeziki ustvarjajo naključne številke med 0 in 1, in kot je razvidno iz prejšnjih primerov, je slednja porazdelitev verjetnosti enotna. V tem primeru je interval, ki ga je treba upoštevati [0,1].

Poljubno vzorčenje porazdelitve

Če imate eksperiment, v katerem imajo dogodki pravilno, kot je razloženo zgoraj, lahko načeloma dodelite vsaki isti verjetnosti pojavljanja. V tem primeru verjetnostni model enotne porazdelitve zagotavlja informacije za analizo.

Zaokroževanje napak

Enotna porazdelitev se uporablja tudi pri zaokroževanju razlik med opazovanimi vrednostmi in resničnimi vrednostmi spremenljivke, ob predpostavki, da je enakomerna porazdelitev napake v določenem intervalu po zaokroževanju običajno od -0,5 do +0.5.

Reference

1. Berenson, m. 1985. Statistični podatki za upravo in ekonomijo. Interameriški s.Do.
2. Canavos, g. 1988. Verjetnost in statistika: aplikacije in metode. McGraw Hill.
3. Devore, j. 2012. Verjetnost in statistika za inženirstvo in znanost. 8. Izdaja. Cengage.
4. Levin, r. 1988. Statistika za skrbnike. 2. mesto. Izdaja. Dvorana Prentice.
5. Triola, m. 2010. Osnovna statistika. 11. Izdaja. Addison Wesley.
6. Walpole, r. 2007. Verjetnost in statistika za inženirstvo in znanost. Pearson.