Dinamika primerov sistema delcev, vaje

The Dinamika sistema delcev Sestavljen je iz uporabe Newtonovih zakonov od gibanja do niza delcev, ki jih je mogoče diskretno (delce je mogoče šteti) ali da je del razširjenega predmeta, v tem primeru je sistem neprekinjen.

Če želite razložiti gibanje sistema delcev, je neprijetno analizirati vsakega posebej in videti, kaj sile delujejo na njem. Namesto tega je definirana reprezentativna točka niza, imenovana Masovni center.

Opisovanje gibanja množičnega centra ponuja zelo uspešno panoramo globalnega gibanja sklopa, prav tako omogoča uporabo Newtonovih zakonov, ki so podobni, ko predmet velja za delček brez dimenzij.

Ta zadnji model, imenovan Model delcev, Dobro je opisati prevode in tudi kadar ni treba upoštevati dimenzij predmeta. Toda navadni predmeti so velikost in če imajo tudi vrtenje, je treba upoštevati točke, na katerih se sile uporabljajo.

[TOC]

Primeri

Zemlja in luna

Ilustracija Zemlje in lune

Nabor diskretnih delcev m₁, m₂, m₃... ki se sčasoma premika glede na izvor koordinatnega sistema, zaradi neke posledične sile, ki deluje nanje, je dober primer sistema delcev.

Zemlja se lahko šteje za en delček in luna drugega, nato pa sta oba sistem dveh delcev pod delovanjem sile teže sonca.

Podaljšani predmeti

Oseba, žival ali kateri koli predmet okolja se lahko šteje. To je neprekinjen sistem, vendar je ob upoštevanju določenih pomislekov njegovo zdravljenje enako kot pri diskretnem sistemu.

Lahko vam služi: kakšna je entalpija treninga? (Z vajami)

Tu so podrobnosti.

Masno središče sistema delcev

Za začetek preučevanja sistema delcev morate najti masno središče (CM), kar je točka, kjer je koncentracija celotna masa sistema.

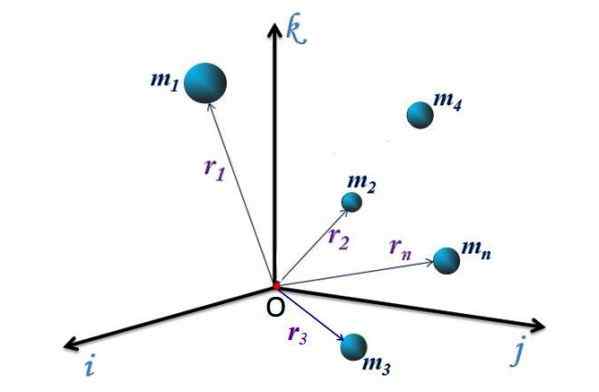
Slika 1. Sistem delcev v referenčnem sistemu XYZ. Vir: f. Zapata.

Za diskretni sistem slike 1 n delci, vsak ima položaj, usmerjen od izvora ali koordinatnega sistema do točke P (x, y, z), kjer je delček. Ti vektorji so označeni kot r₁, r₂, r₃.. r_n.

CM koordinate se izračunajo po naslednjih enačbah:

Kjer je vsaka masa seta predstavljena kot m₁, m₂, m₃... m_n. Upoštevajte, da vsota ∑ m_Yo Je enakovreden skupni masi m kompleta. Če je sistem neprekinjen, se povzetki nadomestijo z integrali.

Vsak od pravokotnih naslovov predstavlja enotni vektorji Yo, J in k, Zato je vektor položaja CM označen r_Cm, Lahko se izrazi z:

r_Cm = x_Cm Yo + in_Cm J + z_Cm k

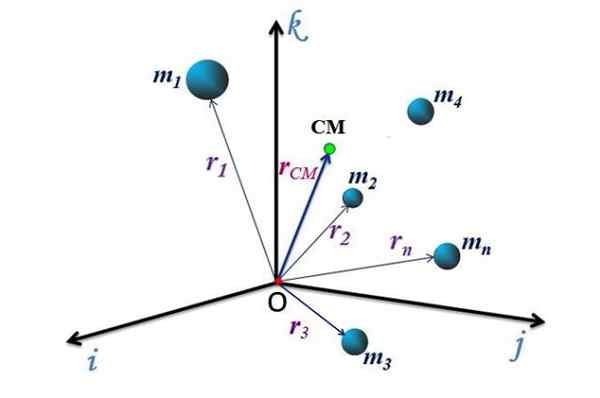Slika 2. Množična lokacija sistema delcev. Vir: f. Zapata.

CM gibanje

Ko je znana lokacija masnega središča, se uporabijo znane enačbe gibanja. Hitrost CM je prva izhaja iz položaja glede na čas:

V tem primeru ima sistem skupno količino gibanja Str ki se izračuna kot produkt celotne mase sistema in hitrosti masnega centra:

Lahko vam služi: fizična usmeritev: značilnosti, vrste, primeri in vaje

Str = M ∙v_Cm

Lahko pa celotno količino sistema izračunamo neposredno:

Str = m₁v₁ + m₂v₂ + m₃v₃ +.. . = ∑ m_Yo v_Yo

Medtem ko je pospešek CM izpeljana hitrost:

Moč na cm

Sile, ki delujejo na sistem delcev, so lahko:

• Notranje sile zaradi interakcij med istimi delci.
• Zunanje sile, ki jih povzročijo agenti, ki so zunaj sistema.

Ker so notranje sile predstavljene s pari, enake razsežnosti in smeri, vendar nasprotna čutila, je po Newtonovem tretjem zakonu izpolnjeno:

∑ F_int = 0

Zato notranje sile ne spreminjajo gibanja celote, vendar so zelo pomembne za določitev notranje energije.

Če je sistem izoliran in zunanjih sil ni, po Newtonovem prvem zakonu, je masovni center v mirovanju ali se premika z enotnim pravokotnim gibanjem. V nasprotnem primeru središče mase doživlja pospeševanje:

∑ F_ext = M ∙do_Cm

Kjer je m skupna masa sistema. Prejšnja enačba je mogoče zapisati tako:

In to pomeni, da je zunanja sila enakovredna začasni razliki v količini gibanja, še en način izražanja Newtonovega drugega zakona in istega, ki ga je v svoji knjigi uporabljal znani angleški fizik Načelo.

Vaja rešena

Masno središče sistema 2 delcev je na osi x v določenem trenutku, v položaju x = 2.0 m in premikanje s hitrostjo 5.0 m/s v isti smeri in pozitivno. Če je eden od delcev pri izvoru in drugem, mase 0.1 kg, v mirovanju pri x = 8.0 m, izračunajte:

Vam lahko služi: diamagnetizem: materiali, aplikacije, primeri

a) masa delca, ki je na izvoru.

b) Količina gibanja sistema

c) Kakšna hitrost je delček, ki je pri izvoru?

Rešitev

Iz enačbe za položaj masnega centra:

r_Cm = x_Cm Yo + in_Cm J + z_Cm K = 2.0 m Yo

Ker ima CM samo koordinato X, se uporablja prva trio enačba prej:

Koordinate so zdaj zamenjane, če je delček označen na izvoru, kot sta številka 1, drugi pa na primer številka 2, so številčni podatki:

x₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Ostati:

= 0.3kg

Rešitev b

Količina gibanja sistema se izračuna z:

Str = M ∙v_Cm

Skupna masa m je enaka:

M = 0.3 kg + 0.1 kg = 0.4 kg

Zato:

Str = 0.4 kg ∙ 5.0 m/s Yo = 2 kg.gospa Yo

Rešitev c

Enačbe za Str od dvostranskega sistema se razčisti v₁, Ker so drugi podatki znani, ker izjava pravi, da je delček 2 v mirovanju, torej:

v₂ = 0 

In Str Preprosto je:

Str = m₁v₁

v₁ = Str / m₁ = 2 kg.gospa Yo / 0.3kg = 6.67 m/s Yo

Reference

1. Univerza Duke. Sistemi delcev. Okrevano od: webhome.Phy.vojvoda.Edu.
2. Rex, a. 2011. Osnove fizike. Pearson.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
5. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.