Kotni premik

Kaj je kotni premik?

On Kotni premik Sprememba ali sprememba kotnega položaja je objekt v rotacijskem doživljanju, ki se običajno meri v radianih ali kakršnem koli drugem ukrepu za zavoje, kot so ocene ali revolucije.

Ko se objekt vrti okoli fiksne osi, se njegov kotni premik določi z merjenjem kota, premetanega z črto, ki poteka skozi katero koli točko telesa, ki seka osi vrtenja, to je radialna črta.

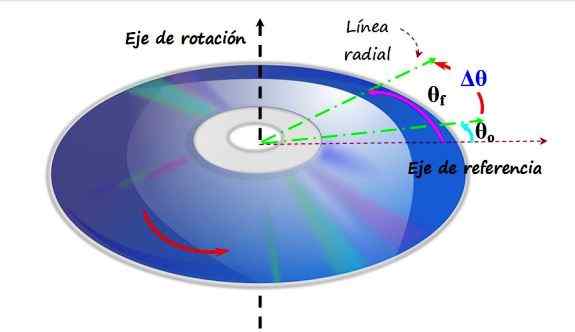Kompaktni disk ali CD se vrti v antihoranantni smeri okoli navpične rotacijske osi. Pri prehodu iz kota θo v θf je rečeno, da je doživel kotni premik. Vir: f. Zapata.

Na zgornji sliki je CD, ki se vrti v protirožni smeri, saj je njegova os vrtenja navpična os. Na ravnini CD -ja je nameščena referenčna os, ki ustreza radianom kotom 0 ali 0. Zelena črta je radialna črta, ki sprva tvori kot θ_tudi S referenco. To je vaš začetni položaj.

Kasneje se zelena črta premakne v nov položaj, imenovan θ_F, In izkušnja, imenovana Δθ, je preprosto:

Δθ = θ_F - θ_tudi

Vsaka točka P doživi enak kotni premik v določenem časovnem intervalu, razen središča, kjer je osi vrtenja in ostane v mirovanju.

Formule in enačbe

Obstaja predmet, ki se vrti okoli fiksne osi ali ki bralcu pusti zaslon. In znotraj njega je točka P, ki se nahaja na razdalji r vrtilne osi in opisuje obod radia R.

To je razvidno iz naslednje slike, ki prikazuje rezalni predmet, ki ga vidimo v nasprotju z iglami. Zadevna točka je v kotnem položaju θ, merjena iz referenčne osi, kar je v tem primeru vodoravna os.

Vam lahko služi: načelo aditiva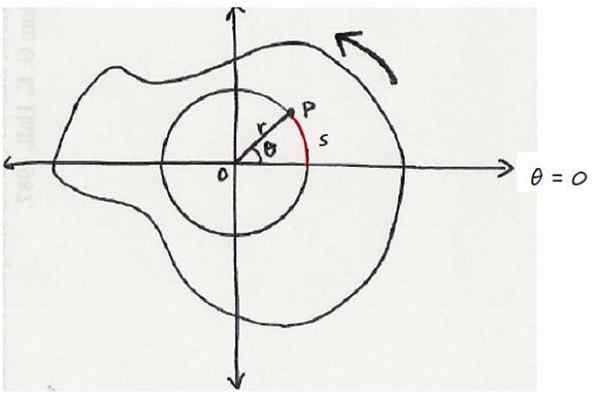Predmet, ki se vrti v protirodnem smislu. Os vrtenja pride pravokotno na zaslonu. Vir: Wikimedia Commons.

Po konvenciji je za vrtenje v antihoraričnem smislu dodeljen pozitiven smisel, medtem ko ima vrtenje v urniku negativen znak.

Ko točka P prisega na kot θ, hkrati potuje z loki. Ker je θ osrednji kot, saj njegova vrha zavzema središče oboda, je izpolnjeno:

Z θ, izraženim v radianih.

Kotni premik je:

Δθ = θ_finale  - θ_začetno

Na primer, če je P začel z θ_začetno = 0 rad in potem je v θ_finale = 0.8 rad, njegov kotni premik je iz:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Druge točke predmeta lahko zasedajo različne kotne položaje, vendar vse doživljajo isti kotni premik. Vendar najbolj oddaljeni delci iz središča potujejo na večje razdalje, saj je s = r⋅θ.

Koti merijo

V vrtenju je običajno najti kote, merjene v radianih, vendar jih najdemo tudi v stopinjah in revolucijah ali zavojih. Pri reševanju problemov je treba prestaviti iz teh enot na radiane.

1 revolucija je enaka popolnemu zavoju, torej ko je popoln zavoj pokvarjen, je dopolnil 360 ° in ti so enakovredni 2π radianom, saj je v tem primeru točka obiskala lok, enak 2πr:

Toda poenostavitev je mogoče prejšnjo enakovrednost izraziti na naslednji način:

π radianes = 180 °

Kako se izračuna kotni premik?

Kotni premik je mogoče analogno izračunati tako, da se premik v gibanju izračuna v dimenziji, po določenem modelu gibanja. Za to je povprečna kotna hitrost opredeljena kot kotni premik Δθ v določenem časovnem intervalu ΔT:

Kjer je povprečna kotna hitrost označena kot ω_m in je dana v radianih/s v enotah mednarodnega sistema, če.

Vam lahko služi: kako dobiti kot trikotnika? (Primer)

Takojšnja kotna hitrost je meja povprečne kotne hitrosti, kadar ΔT → 0:

To pomeni, da je prvi izhajal iz kotnega položaja glede na čas. Po drugi strani je mogoče določiti kotni pospešek, označeno kot α, ki je enakovredna derivatu ali hitrosti sprememb kotne hitrosti glede na čas:

Ki jo lahko razlagamo tudi kot drugo, ki izhaja iz kotnega položaja glede na čas.

Pomembno je, da se lahko v analogiji vzpostavijo dva modela gibanja z pravokotnimi gibi, saj čeprav se rotacije izvajajo v ravnini, zadostuje ena sama kotna koordinata za določitev položaja katere koli točke predmeta.

Enotno krožno gibanje

V enotnem krožnem gibanju je kotna hitrost konstantna, to je, da je povprečna kotna hitrost enaka takojšnji kotni hitrosti. Ker je kotni pospešek α enak 0, lahko za položaj napišete naslednjo enačbo kot funkcijo časa:

θ = θ_tudi + ωt

Kjer θ_tudi To je začetni položaj mobilnega telefona.

Enakomerno pospešeno krožno gibanje

V tem primeru je kotni pospešek α konstanten in po analogiji z enakomerno raznolikim pravokotnim gibanjem lahko zapišemo naslednje enačbe:

• θ = θ_tudi + Ω_tudi T + ½ αT²
• Ω = ω_tudi + αT 
• Ω² = Ω_tudi² + 2α ∙ Δθ

Vaja rešena

Prva vaja

Domnevamo lahko, da je zemlja togi objekt, ki se vrti na fiksni osi in da je njegovo vrtenje skoraj enakomerno. V časovnem intervalu ΔT = 12 h Poiščite:

a) Kotni premik zemlje

b) Vaša kotna hitrost

c) kotni pospešek v tem časovnem intervalu.

Rešitev

Če veste, da se v 24 urah Zemlja popolnoma obrne na svojo osi, boste v 12 urah zavrnili polovico kroga, torej π radianes. Če se šteje za del θ_začetno = 0 rad, potem je njegov kotni premik:

Lahko vam služi: Multiplikativno načelo: Tehnike štetja in primeri

Δθ = π radians

Rešitev b

Ker je vrtenje enakomerno, je kotna hitrost količnik med kotnim premikom in časom, poleg tega pa 1 ura = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 RAD/S.

Rešitev c

Kotni pospešek je ničen, saj je vrtenje zemlje enakomerno.

Druga vaja

Juan je na krožni atletski progi pretekel razdaljo 35 metrov, katere polmer je enak 7 metrom. Izračunajte kotni premik, ki ga je naredil Juan.

Rešitev

Ker je znana razdalja potovanega loka in polmer oboda, lahko drugo formulo uporabimo za spoznavanje kotnega premika, ki ga je naredil Juan. Uporaba zgoraj opisane formule morate θ = 35/7 = 5 radianov.

Tretja vaja

Če mora Mario v svojem vozilu, polovico krožne dirkaške proge, kaj je kotni premik, ki ga je storil Mario?

Rešitev

V tej vaji bo veljala prva formula. Ker je znano, da je Mario potoval polovico proge, lahko domnevamo, da je dirko začel pod kotom 0 ° in ko je dosegel polovico oboda, je potoval 180 °. Zato je odgovor 180 ° -0 ° = 180 ° = π radianov.

Četrta vaja

Marija ima krožni bazen. Vaš pes teče po bazenu, ki potuje na razdalji 18 metrov. Če je polmer bazena 3 metre, kakšen je kotni premik, ki ga je ustvaril Marijin hišni ljubljenček?

Rešitev

Ker je bazen krožen in njegov polmer je znan, lahko nadaljujete z uporabo druge formule.

Znano je, da je polmer enak 3 metrom, razdalja, ki jo prevozi hišni ljubljenček. Zato je izvedeni kotni premik enak θ = 18/3 = 6 radianov.

Reference

1. Katz, d. 2013. Fizika za znanstvenike in inženirje. Temelje in povezave. Cengage učenje.
2. Rex, a. 2011. Osnove fizike. Pearson.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
5. Tipler, str. (2006). Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.