Neenakost demonstracijskega trikotnika, primeri, rešene vaje

Se imenuje Neenakost trikotnika do nepremičnine, ki izpolnjujeta dve realni številki, sestavljeni iz absolutne vrednosti njegove vsote, je vedno manjša ali enaka vsoti njegovih absolutnih vrednosti. Ta lastnost je znana tudi kot Minkowski neenakost ali trikotna neenakost.

Ta lastnost števil se imenuje trikotna neenakost, ker se v trikotnikih zgodi, da je dolžina ene strani vedno manjša ali enaka vsoti drugih dveh, tudi če ta neenakost ne velja vedno na področju trikotnikov.

Slika 1. Absolutna vrednost vsote dveh števil je vedno manjša ali enaka vsoti njegovih absolutnih vrednosti. (Pripravil R. Pérez)

V realnem številu obstaja več demonstracij trikotne neenakosti, vendar bomo v tem primeru izbrali a na podlagi lastnosti absolutne vrednosti in kvadratnega binoma.

Teorem: Za vse par številk do in b Pripadati resničnim številkam, mora:

| A + B | ≤ | a | + | b |

[TOC]

Demonstracija

Začnemo z upoštevanjem prvega člana neenakosti, ki bo posekan:

| A + B |^2 = (A + B)^2 = A^2 + 2 A B + B^2 (EC. 1)

V prejšnjem koraku je bila lastnost uporabljena, da je poljubno število visokih na kvadratu enaka absolutni vrednosti omenjene številke visoko na kvadrat, to je: | x |^2 = x^2. Uporabljen je bil tudi razvoj kvadratnega binoma.

Vse številke x Je manjša ali enaka svoji absolutni vrednosti. Če je številka pozitivna, je vredna enakosti, če pa je številka negativna, bo vedno manjša od pozitivnega števila. V tem primeru lastna absolutna vrednost, to pomeni, da je to mogoče navesti x ≤ | x |.

Vam lahko služi: nelinearno programiranje: metode in vaje

Izdelek (a b) Je številka, zato se uporablja (a b) ≤ | a b |. Ko se ta lastnost uporablja za (EC. 1) Imamo:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | a b | + B^2 (EC. 2)

Ob upoštevanju tega | A b | = | A || b | LA (EC. 2) Lahko ga zapišemo na naslednji način:

 | A + B |^2 ≤ A^2 + 2 | A || b | + B^2 (EC. 3)

Toda kot smo že rekli, da je kvadrat števila enak absolutni vrednosti številke visoke na kvadrat, potem je mogoče enačbo 3 ponovno napisati na naslednji način:

 | A + b |^2 ≤ | a |^2 + 2 | a | | b | + | B |^2 (EC. 4)

V drugem članu neenakosti je prepoznan izjemen izdelek, ki pri uporabi vodi do:

 | A + b |^2 ≤ (| a | + | b |)^2 (EC. 5)

V prejšnjem izrazu je treba opozoriti, da so vrednosti, ki jih je treba zvišati na obeh članih neenakosti, tudi pozitivne, da je treba izpolniti tudi:

 | A + B | ≤ (| a |+ | b |) (EC. 6)

Prejšnji izraz je točno tisto, kar ste želeli pokazati.

Primeri

Nato bomo z več primeri preverili trikotno neenakost.

Primer 1

Vrednost je vzeta a = 2 in vrednost b = 5, to je tako pozitivna številka in preverimo, ali je neenakost izpolnjena ali ne.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Enakost je preverjena, zato je bil izpolnjen teorem o neenakosti trikotnika.

Primer 2

Naslednje vrednosti so izbrane A = 2 in B = -5, torej pozitivno število in drugo negativno, preverimo, ali je neenakost izpolnjena ali ne.

Vam lahko služi: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Neenakost je izpolnjena, zato je bil preverjen trikotni teorem o neenakosti.

Primer 3

Vrednost je vzeta a = -2 in vrednost b = 5, to pomeni negativno število in drugo pozitivno, preverimo, ali je neenakost izpolnjena ali ne.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Neenakost je preverjena, zato je teorem izpolnjen.

Primer 4

Izbrani so naslednje vrednosti A = -2 in B = -5, to je tako negativna številka in preverimo, ali je neenakost izpolnjena ali ne.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Enakost je preverjena, zato je teorem Minkowsk neenakosti izpolnjen.

Primer 5

Vrednost je vzeta a = 0 in vrednost b = 5, to pomeni nič in drugo pozitivno, potem preverimo, ali je neenakost izpolnjena ali ne.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Enakost je izpolnjena, zato je bil preverjen teorem o neenakosti trikotnika.

Primer 6

Vrednost je vzeta a = 0 in vrednost b = -7, to pomeni nič in drugo pozitivno, potem preverimo, ali je neenakost izpolnjena ali ne.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Enakost je preverjena, zato je bil izpolnjen trikotni teorem neenakosti.

Rešene vaje

V naslednjih vajah geometrijsko predstavlja neenakost trikotnika ali neenakosti Minkowskega za številke A in B.

Vam lahko služi: papomudas

Številka A bo predstavljena kot segment na osi x, njegov izvor ali sovpada z ničlo osi x in drugi konec segmenta (v točki P) bo v pozitivni smeri (na desni) osi x, če je a> 0, ampak do < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Podobno bo številka B predstavljena kot segment, katerega izvor je na točki P. Drugi konec, torej točka, ki bo desno od P, če je B pozitiven (B> 0) in točka q bo | b | enote levo od p, če B<0.

Vaja 1

Grafično predstavljajo neenakost trikotnika za A = 5 in B = 3 | A + B | ≤ | a | + | b |, biti C = a + b. 

Rešitev 1: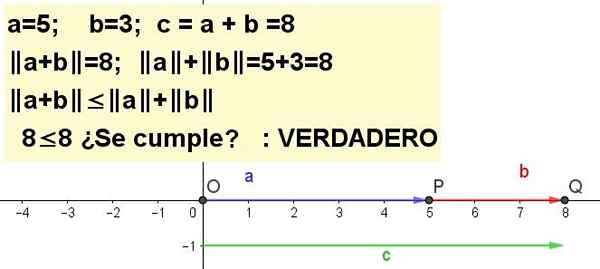

Vaja 2

Naredite graf trikotne neenakosti za A = 5 in B = -3. 

| A + B | ≤ | a | + | b |, biti C = a + b.

Rešitev 2:

Vaja 3

Grafirajte neenakost trikotnika za A = -5 in B = 3.

| A + B | ≤ | a | + | b |, biti C = a + b. 

Rešitev 3: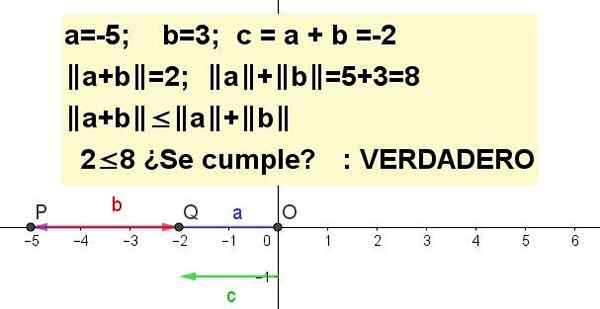

Vaja 4

Grafirajte trikotno neenakost za A = -5 in B = -3.

| A + B | ≤ | a | + | b |, biti C = a + b.

Rešitev 4: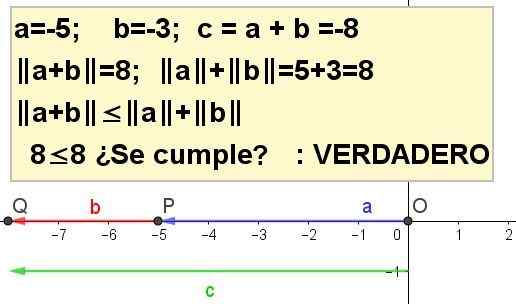

Reference

1. In. Whitesitt. (1980).Boolejska algebra in njegove aplikacije . Continental uredništvo c. Do.
2. Mícheal ali 'searcoid.(2003) Elementi abstraktne analize ... Oddelek za matematiko. University College Dublin, Beldfield, Dublind.
3. J. Van Wyk. (2006) Matematika in inženiring iz računalništva. Inštitut za računalniške znanosti in tehnologijo. Nacionalni urad za standarde. Washington, d. C. 20234
4. Eric Lehman. Matematika za računalništvo.  Google inc.
5. F Thomson Leighton (1980). Izračun. Oddelek za matematiko in računalništvo in laboratorij AI, Massachussetts Institute of Technology.
6. Akademija Khan. Teorem trikotnika neenakosti. Okreval od: Khanacademy.org
7. Wikipedija. Trikotna neenakost. Okrevano od: je. Wikipedija.com