Izhaja iz izračuna Cotangent, demonstracije, vaje

The Izpeljan Cotangent Je enako nasprotju s kvadratom žetve "-csc²". Ta formula je posledica izpeljanih zakonov po definiciji in diferenciacije trigonometričnih funkcij. Označeno je na naslednji način:

D (ctg u) = -csc² ali . du

Kjer "du" simbolizira izraz, ki izhaja iz funkcije argumenta, glede na neodvisno spremenljivko.

Vir: Pixabay.com

[TOC]

Kako se izračuna?

Postopek za razvoj teh derivatov je precej preprost. Samo določite argument in vrsto funkcije, ki jo predstavlja.

Na primer, izraz CTG (f/g) predstavlja delitev v svojem argumentu. Po razvoju zadrge bo to potrebovalo razlikovanje glede U/V.

Cotangent je vzajemna funkcija tangenta. Algebraično to pomeni, da:

(1/tg x) = ctg x

Ctg x = cos x / sen x

Nepravilno je reči, da je funkcija Cotangent "obratna" tangenta. To je zato, ker je obratna funkcija tangenta po definiciji tangentni lok.

(TG^-1 x) = arctg x

Po besedah ​​pitagorejske trigonometrije je Cotangent vključen v naslednje razdelke:

Ctg x = (cos x) / (sin x)

CTG² X + 1 = CSC² x

Po analitični trigonometriji se odziva na naslednje identitete:

Ctg (a + b) = (1 - tg a . TG B) / (TG A + TG B)

Ctg (a - b) = (1 + tg a . TG B) / (TG A - TG B)

CTG (2A) = (1 - TG² a) / (2tg a)

Značilnosti kotangentne funkcije

Analizirati je treba različne značilnosti funkcije f (x) = ctg x, da lahko določimo potrebne vidike za preučevanje njegove razlike in uporabe.

Navpične asimptote

Funkcija Cotangengent ni definirana v vrednostih, zaradi katerih je izraz "senx" nič. Zaradi enakovrednega CTG x = (cos x) / (sin x) bo imel nedoločnost v vseh "nπ" z n, ki pripada celim številom.

Lahko vam služi: analitična geometrija

To pomeni, da bo v vsaki od teh vrednosti x = nπ navpična asimptota. Ko se vrednost kotangenta približa in ko se približuje pravici, se bo funkcija povečala v nedogled.

Domena

Domena funkcije Cotangent je izražena z nizom x ∈ R / x ≠ nπ, n ∈ Z. To se bere kot "x, ki spada v nabor resničnih števil, tako da je x drugačen od nπ, pri čemer N pripada celotnemu številu".

Domet

Ranka funkcije Cotangent zajema od manj do več neskončnosti. Zato je mogoče sklepati, da je njegov uvrstitev nabor resničnih N številk.

Frekvenca

Funkcija Cotangenge je periodična in njegovo obdobje je enako π. Na ta način je izpolnjena enakost ctg x = ctg (x + nπ), kjer n pripada Z.

Vedenje

To je neparna funkcija, saj ctg (-x) = - ctg x. Na ta način je znano, da funkcija predstavlja simetrijo glede na koordinatni izvor. Prav tako predstavlja zmanjšanje vsakega intervala, ki se nahaja med dvema zaporednima navpičnimi asimptoti.

Nima najvišjih ali najmanjših vrednosti, ker imajo njihovi pristopi do vertikalnih asimptotov vedenje, kjer funkcija raste ali se zmanjšuje v nedogled.

Zero ali korenine kotangentne funkcije najdemo v neparnih večkratnikih π/2. To pomeni, da je CTG x = 0 izpolnjen v vrednostih obrazca x = nπ/2 z celoto.

Demonstracija

Obstajata dva načina za prikaz izpeljave funkcije Cotangent.

Trigonometrična diferencialna demonstracija

Derivat funkcije Cotangent je dokazan iz njegovega ekvivalenta v dojkih in Cosenosu.

Lahko vam služi: Boolean Algebra: Zgodovina, teoremi in postulati, primeri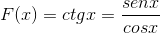

Gre za izpeljavo oddelka za funkcije

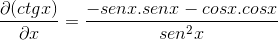
Po pridobivanju dejavnikov so razvrščeni in pitagorejske identitete poskušajo posnemati

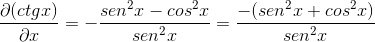
Zamenjava identitet in uporaba vzajemnosti Izraz dobimo

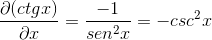
Opredelitev definicije izpeljane

Naslednji izraz ustreza derivatu po definiciji. Kjer se razdalja med dvema točkama funkcije približuje nič.

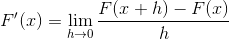
Zamenjava za cotangente morate:

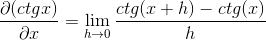
Za vsoto argumentov in vzajemnosti veljajo identitete

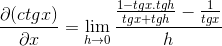
Del števca deluje tradicionalno

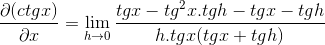
Odpravljanje nasprotnih elementov in risanje skupnega faktorja

Uporaba pitagorejskih identitet in vzajemnosti

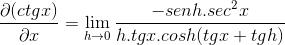
Elementi, ocenjeni v x, so konstantni glede na mejo, zato lahko argument tega pustijo. Nato se uporabijo trigonometrične meje.

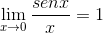
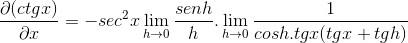
Omejitev je ocenjena

Potem je spremenjen, dokler ne dosežete želene vrednosti

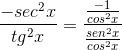
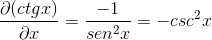
To je kotangente derivat pokazal kot nasprotje kvadrata kombajna.

Rešene vaje

Vaja 1

V skladu s funkcijo f (x) določite izraz f '(x)

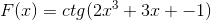
Ustrezna izpeljava se uporablja v zvezi s pravilom verige

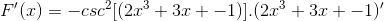
Izpeljava argumenta

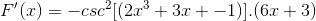
Včasih je treba uporabiti vzajemne ali trigonometrične identitete za prilagajanje rešitev.

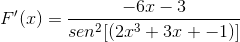
Vaja 2

Določite diferencialni izraz, ki ustreza F (x)

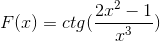
V skladu s formulo izpeljave in spoštovanjem pravila verige

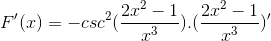
Argument je izpeljan, preostali

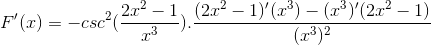
Izvedba vseh elementov

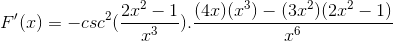
Na tradicionalen način delujejo izdelki iste baze

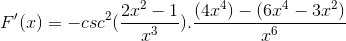
Dodani so isti elementi in izvlečen je skupni faktor

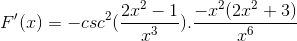
Znaki so poenostavljeni in upravljani. Popuščanje popolnoma izpeljanemu izrazu

Vam lahko služi: razlika med skupno frakcijo in decimalno številko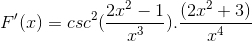

Reference

1. Trigonometrična serija, 1. zvezek. Do. Zygmund. Cambridge University Press, 2002
2. Izračun ene same spremenljivke. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. november. 2008
3. Izračun s trigonometrijo in analitično geometrijo. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saksonski založniki, 1988
4. Multivariabilna analiza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. december. 2010
5. Sistemska dinamika: modeliranje, simulacija in nadzor mehatronskih sistemov. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
6. Calculus: matematika in modeliranje. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick VITRAY. Addison Wesley Longman, 1. januar. 1999