Togo telo

Kaj je togo telo?

Togo telo je materialni objekt, katerega delci vedno ostanejo v enakih relativnih položajih. Zato je predmet, ki ni deformiran, kakovost, ki jo pripisujejo intenzivni kohezijski sili, ki ohranjajo delce na mestu.

Pravzaprav se delci katerega koli telesa, ki so podvrženi zunanjim silam, vibrirajo ali premikajo, zato je predmet do neke mere vedno deformiran, vendar so ti učinki običajno majhni.

Ko je temu tako, lahko domnevamo, da je telo togo in ima zelo dober pristop k svojemu vedenju, tudi če je idealizacija.

Vrste togih teles

Lahko ločite dve vrsti togega telesa:

• Tisti, katerih delci so v diskretnih količinah, to pomeni, da lahko štejejo. Na primer, dve kovinski sferi, povezani s tanko in svetlo palico. Če je palica dovolj toga, da se ne upogne, se sistem šteje za togo telo.
• Tisti, ki so neprekinjeni, kar pomeni, da so delci, ki jih sestavljajo. Vsakodnevni in naravni predmeti so dobri primeri: kamni, pohištvo in drugi, pa tudi zemlja in druge nebesne kamnine Rocky.

Togo gibanje in dinamika telesa

Tako kot predmeti, ki veljajo za delce, se lahko tudi toga telesa prenesejo, zasukajo in imajo splošnejše gibanje, ki združuje prevod in vrtenje.

Za preučevanje prevoda ni potrebno.

Ti premiki prevajanja in vrtenja so lahko:

• Neodvisno, kot v primeru planetov, ki imajo vrtilno gibanje okoli svoje osi (šteje se za fiksno) in drugega prevoda okoli sonca, vendar hitrosti vsakega niso povezane.
• Zlomljena trash, če sta kotna hitrost in hitrost prevajanja središča mase. V tem primeru je os vrtenja mobilna, kot v primeru valja, ki se spušča, ne da bi zdrsnil z nagnjenim naklonom.

Lahko vam služi: prvi zakon termodinamike: formule, enačbe, primeri

Dinamika toge trdne

Naslednje veličine so pomembne v dinamiki toge trde:

Masovni center

Središče mase je točka, kjer se šteje, da je celotna masa telesa koncentrirana. Če gre za homogeno in simetrično telo, kot kroglo, središče mase sovpada z geometrijskim središčem.

Inercijski trenutek

Ta skalarna velikost je vrednost rotacijske vztrajnosti ali upora, ki nasprotuje predmetu, da se vrti okoli določene osi. V celoti je odvisno od geometrije predmeta in njegove mase, zato je v določenih primerih lažje obrniti nekatere osi kot na druge.

Za telesa z dobro definiranimi geometrijskimi oblikami obstajajo tabele s trenutki vztrajnosti glede na osi simetrije, na primer tisto, ki gre skozi masno središče. S temi informacijami in teoremi, povezanimi s trenutkom vztrajnosti, je mogoče trenutke glede na druge osi enostavno izračunati.

Sile in navor ali navor

Sile morajo premikati telo. Če se togo središče trdne mase premakne, je enačba gibanja po Newtonovem drugem zakonu:

F_Mreža = M ∙do_cm

Kje:

-Neto sila je F_Mreža

-M je masa

-Pospešek masnega središča je do_cm

Vendar pa vse uporabljene sile ne povzročajo prekinitve predmeta. Za to je potreben navor ali navor, ki pravi, kako učinkovito je rotacijsko delovanje sile. Opredeljen je kot vektorski izdelek med položajem vektorja r Glede določene točke in sile F pod vprašajem. Označuje ga grško pismo τ (S krepko črko je tudi vektor):

Vam lahko služi: eliptično gibanje

τ = r × F

V mednarodnem sistemu je navorna enota N⋅m (Newton na meter).

V mnogih primerih je rotacijsko gibanje okoli osi, ki poteka skozi središče mase, opisano s analogno enačbo Newtonovemu drugemu zakonu:

Kadar se naročnik "Z" nanaša na osi vrtenja, ki poteka skozi os simetrije, fiksirane ali premikanja, vendar brez spreminjanja smeri in_cm To je inercijski trenutek glede na središče mase in α_z To je kotni pospešek telesa. Poletje zajema vse zunanje trenutke okoli osi z.

Kinetična energija toge trdne snovi

Gibanje togega telesa je opisano s prevodi središča mase in rotacij okoli te točke, zato ima njegova kinetična energija oba prispevka.

Naj K kinetična energija telesa, V_cm Hitrost masnega središča, m masa telesa in_cm njen vztrajnost glede na središče mase in ω kotne hitrosti. Lahko je dokazano, da je kinetična energija:

K = ½ mV_cm² + ½ i_cm Ω²

Opazimo, da je drugi izraz desno rotacijski analog izraza leve. Tam ima inercijski trenutek enako vlogo kot masa, medtem ko ima kotna hitrost enako vlogo kot linearna hitrost.

Primeri v vsakdanjem življenju

Fizično nihalo

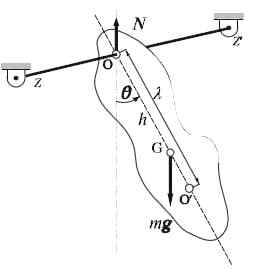Fizično nihalo

Fizično nihalo ali resnično nihalo je zelo enostavno graditi: sestavljen je iz toge trdne snovi, kot je palica ali palica, prosto niha okoli vodoravne osi. Os vrtenja ne prečka središča mase predmeta in to lahko načeloma oblikuje.

Vam lahko služi: termometer upora: značilnosti, delovanje, uporabe

Ta nihala se razlikuje od preprostega nihala, ker v slednjem velja, da je masa, ki ga sestavlja.

Kolesarsko kolo

Kolesarsko kolo

Drug dobro znan togi karoserijski primer je kolesarsko kolo, katerega os gre skozi sredino mase, ki prečka sredino kolesa. Dokler se ne naslanjajo na stran ali obrnejo, veljajo enačbe opisane dinamike za opis vašega gibanja.

Žoga za balinanje

Dober primer togega telesa je kroglica za kegljanje

Togi trdni model se zelo dobro prilagodi, da opiše gibanje kroglice za kegljanje na stezi ali ko se valja, ne da bi zdrsnil po povratni rampi.

Yoyo

Yoyo je priljubljena igrača, ki jo je mogoče modelirati kot togo telo

Ta priljubljena igrača je narejena z lesnim ali plastičnim valjem in vrv, preplavljeno v režo, ki jo obdaja.

Valj lahko modeliramo kot togo telo, v katerem napetost v nizu zagotavlja navor vrtenja, medtem ko sta teža (nanesena na sredino mase) in napetost odgovorna za navpični pospešek središča mase.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
3.  Katz, d. 2013. Fizika za znanstvenike in inženirje. Temelje in povezave. Cengage učenje.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
5. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.