Sistem cilindričnih koordinat, spremembe in vaje

The Cilindrične koordinate Služijo za iskanje točk v tridimenzionalnem prostoru in so sestavljene iz radialne koordinate ρ, azimutalne koordinate φ in višinske koordinate z.

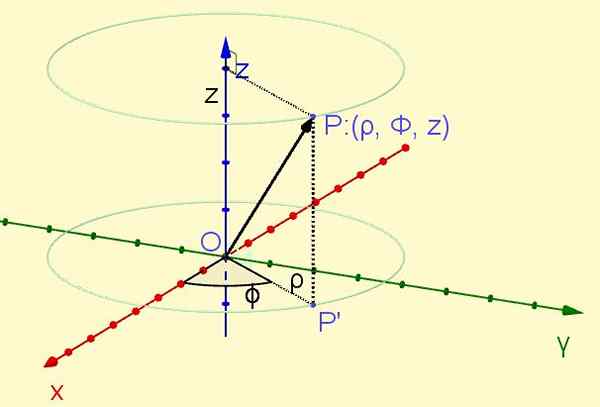
Točka Str Nahaja se v vesolju, ki je ortogonalno projiciran na letalu Xy sproži točko P ' V tej ravnini. Razdalja od izvora do točke P ' definira koordinat ρ, medtem ko kota, ki tvori osi X S polčasom Op ' Določite koordinato φ. Končno koordinata z To je pravokotna projekcija točke Str na osi Z. (Glej sliko 1).

Slika 1. Točka P cilindričnih koordinat (ρ, φ, z). (Lastna izdelava)

Radialna koordinata ρ je vedno pozitivna, azimutalna koordinata φ se spreminja od nič radianov do dveh pi radianov, medtem ko lahko koordinata Z vzame kakršno koli resnično vrednost:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Sprememba koordinat

Relativno preprosto je pridobiti kartezijanske koordinate (x, y, z) iz točke P iz svojih valjastih koordinat (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Lahko pa tudi pridobimo polarne koordinate (ρ, φ, z) na podlagi znanja kartezijanskih koordinat (x, y, z) točke p:

ρ = √ (x² + in²)

φ = arctan (y/x)

z = z

Vektorska osnova v valjastih koordinatah

Osnova valjastih vektorjev je definirana Uρ, Uφ, Uz.

Vektor Uρ Tangenta je do črte φ = ctte in z = ctte (ki se radialno kaže), vektor Uφ je tangenta do črte ρ = ctte in z = ctte in končno Uz Ima isto smer osi z.

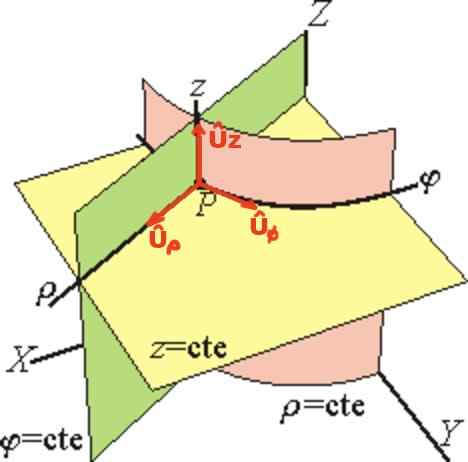Slika 2. Cilindrična koordinatna baza. (Wikimedia Commons)

V bazi cilindrične enote je vektor položaja r Od točke P je napisano tako, kot je ta:

Lahko vam služi: domena in protislovje funkcije (s primeri)

r = ρ Uρ + 0 Uφ + z Uz

Po drugi strani pa neskončno majhni premik dr Od točke P je izražen na naslednji način:

dr = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Podobno je neskončno majhni element volumna DV v valjastih koordinatah:

Dv = ρ dρ dφ dz

Primeri

Obstaja nešteto primerov uporabe in uporabe valjastih koordinat. Na primer v kartografiji Cilindrična projekcija, na podlagi teh koordinat. Obstaja več primerov:

Primer 1

Cilindrične koordinate imajo aplikacije v tehnologiji. Kot primer imate na trdem disku sistem CHS (cilinder-head-sektor) lokacije podatkov, ki je dejansko sestavljen iz več diskov:

- Valj ali skladba ustreza usklajevanju ρ.

- Sektor ustreza φ položaju albuma, ki se vrti na visoko kotna hitrost.

- Glava ustreza položaju z bralno glavo na ustreznem albumu.

Vsak informacijski bajt ima natančen naslov v cilindričnih koordinatah (C, S, H).

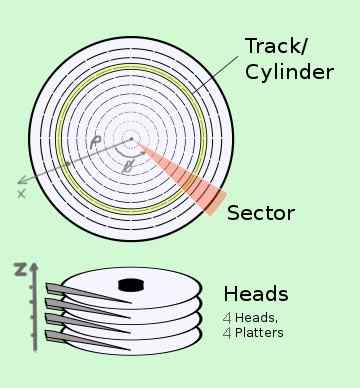Slika 2. Lokacija informacij v cilindričnih koordinatah v sistemu trdega diska. (Wikimedia Commons)

Primer 2

Konstrukcijski žerjavi postavljajo položaj obremenitve v valjastih koordinatah. Vodoravni položaj je določen z razdaljo do osi žerjava ali puščice. Vertikalni položaj obremenitve je določena z Z koordinato višine.

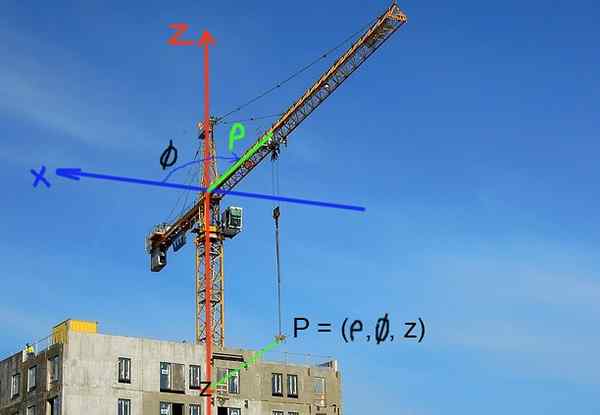Slika 3. Položaj obremenitve v gradbenem žerjanu je mogoče enostavno izraziti v cilindričnih koordinatah. (Pixabay slika - RCOS R. Pérez)

Rešene vaje

Vaja 1

Obstajajo P1 točke cilindričnih koordinat (3, 120 °, -4) in točka P2 cilindričnih koordinat (2, 90 °, 5). Poišči Euclidijska razdalja Med tema dvema točkama.

Vam lahko služi: oddelki, v katerih je ostanek 300

Rešitev: Najprej nadaljujemo z iskanjem kartezijanskih koordinat vsake točke po zgornji formuli, ki se je zgodila.

P1 = (3* cos 120º, 3* Sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

Euclidijska razdalja med P1 in P2 je:

D (P1, P2) = √ ((0 - (-1.5))²+(2 - 2.60²+(5 -(-4))² ) = ..

… √ (2.25+0.36+81) = 9.14

Vaja 2

Točka P ima kartezijanske koordinate (-3, 4, 2). Poiščite ustrezne valjaste koordinate.

Rešitev: Cilindrične koordinate najdemo z zgoraj navedenimi odnosi:

ρ = √ (x² + in²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13 ° + 180 ° = 126.87 °

Z = 2

Ne pozabite, da je funkcija Arcangent MultivalUada periodičnosti 180 °. Poleg tega mora kot φ pripadati drugemu kvadrantu, saj sta koordinata x e y in točke P v tem kvadrantu. To je razlog, zakaj je bil rezultat φ dodan 180 °.

Vaja 3

Izrazite v valjastih koordinatah in v kartezijanskih koordinatah površino radijskega valja 2 in katerih os sovpada z os z.

Rešitev: Razume se, da ima valj neskončno podaljšanje v smeri Z, tako da je enačba omenjene površine v valjastih koordinatah:

ρ = 2

Za pridobitev kartezijanske enačbe cilindrične površine se vzame kvadrat obeh članov prejšnje enačbe:

ρ² = 4

Pomnožimo za 1 člana prejšnje enakosti in uporabimo Temeljna trigonometrična identiteta (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

Razvije oklepaje za pridobitev:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Vam lahko služi: populacija in vzorec

Spomnimo se, da je prva oklepaja (ρ sen (φ)) usklajena in točka v polarnih koordinatah, medtem ko oklepaje (ρ cos (φ)) predstavlja koordinat x, tako da smo ostali Enačba cilindra v kartezijanskih koordinatah:

in² + x² = 2²

Prejšnje enačbe ne bi smeli zamenjati s krogom v ravnini XY, saj bi bilo v tem primeru takšno: in² + x² = 2² ; Z = 0.

Vaja 4

A polmera valj r = 1 m in višina h = 1m ima radialno porazdeljeno maso v skladu z naslednjo enačbo d (ρ) = c (1 - ρ/r), kjer je C konstanta vrednosti C = 1 kg/m³. Poiščite skupno maso valja v kilogramih.

Rešitev: Prva stvar je zavedati, da funkcija D (ρ) predstavlja gostoto volumetrične mase in da je gostujoča masa razporejena v cilindričnih kaskaronih zmanjševanja gostote središča na obrobje. Neskončni element volumna glede na simetrijo problema je:

Dv = ρ dρ 2π h

Od tod boste morali, da bo neskončno majhna masa cilindrične lupine:

Dm = d (ρ) dv

Torej bo skupna masa valja izražena z naslednjim Definiran integral:

M = ∫_tudi^R D (ρ) dv = ∫_tudi^R C (1 - ρ/r) ρ dρ 2π h = 2π h c ∫_tudi^R (1 - ρ/r) ρ dρ

Raztopine navedenega integrala ni težko pridobiti, saj je njen rezultat:

∫_tudi^R (1 - ρ/r) ρ dρ = (⅙) r²

Vključitev tega rezultata v izražanje mase jeklenke je dobimo:

M = 2π H C (⅙) R² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Reference

1. Arfken g in weber h. (2012). Matematične metode za fizike. Obsežen vodnik. 7. izdaja. Akademski tisk. ISBN 978-0-12-384654-9
2. CC izračun. Rešeni cilindrični in sferični koordinatni problemi. Iztegnjeno od: izračun.DC
3. Weisstein, Eric W. „Cilindrične koordinate.”S spleta MathWorld-A Wolfram. Okreval od: Mathworld.Wolfram.com
4. Wikipedija. Cilindrični koordinatni sistem. Pridobljeno iz: v.Wikipedija.com
5. Wikipedija. Vektorska polja v cilindričnih in sferičnih koordinatah. Pridobljeno iz: v.Wikipedija.com