Integracijski konstantni pomen, izračun in primeri

The Konstanta integracije To je dodana vrednost za izračun antiderivativov ali integralov, služi za predstavljanje rešitev, ki sestavljajo primitivno funkcijo. Izraža inherentno dvoumnost, kadar ima katera koli funkcija neskončno število primitivnih.

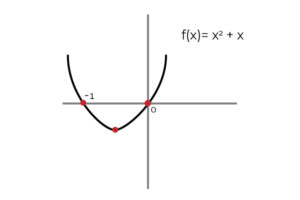
Na primer, če je funkcija vzeta: f (x) = 2x + 1 in dobimo njegovo antiderivacijo:

∫ (2x+1) dx = x² + x + C ; Kje C Je Konstanta integracije in grafično predstavlja navpični prevod med neskončnimi možnostmi primitivnega. Pravilno je reči, da (x² + x) Je a primitivnega f (x).

Vir: Avtor

Na enak način lahko določite (x² + x + C ) kot primitiv F (x).

[TOC]

Inverzna lastnost

Lahko ugotovimo, da ob izpeljanem izrazu (x² + x) Dobimo funkcijo f (x) = 2x + 1. To je posledica obratne lastnosti med izpeljavo in integracijo funkcij. Ta lastnost omogoča pridobivanje integracijskih formul, ki se začnejo z diferenciacijo. Ki omogoča preverjanje integralov z istimi derivati.

Vir: Avtor

Vendar (x² + x) To ni edina funkcija, katere derivat je enak (2x + 1).

1. D (x² + x)/ dx = 2x + 1
2. D (x² + x + 1)/ dx = 2x + 1
3. D (x² + x + 2)/ dx = 2x + 1
4. D (x² + x + 3)/ dx = 2x + 1
5. D (x² + x + C)/ dx = 2x + 1

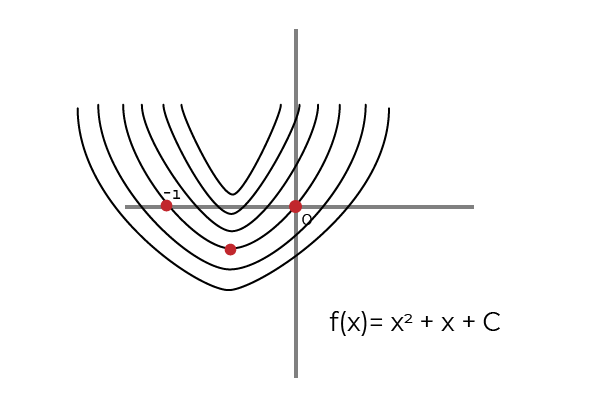
Kjer 1, 2, 3 in 4 predstavljajo posebno primitiv F (x) = 2x + 1. Medtem ko 5 predstavlja nedoločen ali primitivni integral F (x) = 2x + 1.

Vir: Avtor

Primitivno funkcijo dosežemo s pomočjo antiderivacije ali integralnega procesa. Kjer bo f primitiven f, če se izpolni naslednje

• y = ∫ f (x) dx = F (x) + c; C = Konstanta integracije
• F '(x) = f (x)

Cenimo, da ima funkcija en sam izpeljan, za razliko od njenega neskončnega primitivnega, ki je posledica integracije.

Nedoločen integral

 ∫ f (x) dx = f (x) + c

Ustreza družini krivulj z istim vzorcem, ki doživlja neskladnost v vrednosti slik vsake točke (x, y). Vsaka funkcija, ki izpolni ta vzorec, bo individualna primitivna in nabor vseh funkcij je znan kot Nedoločen integral.

Vrednost Konstanta integracije To bo tisto, ki vsako funkcijo razlikuje v praksi.

The Konstanta integracije Predlaga navpični premik v vseh grafih, ki predstavljajo primitivno funkcijo. Kjer opazimo paralelizem med njimi in dejstvo, da C Je vrednost premika.

Glede na skupne prakse Konstanta integracije Označena je s črko "C" po dodajanju, čeprav je v praksi ravnodušna, če konstanta doda ali odšteje. Njegova resnična vrednost lahko najdemo na različne načine v skladu z različnimi začetni pogoji.

Drugi pomeni integracijske konstante

Že je govorilo o tem, kako Konstanta integracije se uporablja v veji integralni računanje; Predstavlja družino krivulj, ki definirajo nedoločen integral. Toda številne druge znanosti in veje so dodelile zelo zanimive in praktične vrednote Konstanta integracije, ki so olajšali razvoj več študij.

Lahko vam služi: Laptoid Trapezoid: Lastnosti, odnosi in formule, primeri

V fizično Konstanta integracije lahko vzame več vrednosti glede na naravo podatkov. Zelo pogost primer je poznati funkcijo V (t) ki predstavlja hitrost delca v primerjavi s časom t. Znano je, da se pri izračunu primitivne V (t) funkcija dobi R (t) ki predstavlja položaj delca v primerjavi s časom.

The Konstanta integracije bo predstavljala vrednost začetnega položaja, torej trenutno t = 0.

Podobno, če je funkcija znana A (t)  ki predstavlja pospešek delca v primerjavi s časom. Primitiv A (t) bo povzročil funkcijo v (t), kjer Konstanta integracije To bo vrednost začetne hitrosti v₀.

V ekonomija, z pridobivanjem primitive stroškovne funkcije z integracijo. The Konstanta integracije bo predstavljal fiksne stroške. In toliko drugih aplikacij, ki zaslužijo diferencialno in integralno računanje.

Kako se izračuna konstanta integracije?

Za izračun Konstanta integracije, Vedno bo treba vedeti začetni pogoji. Ki so odgovorni za določitev, kateri od možnih primitivnih je ustrezen.

V mnogih aplikacijah se obravnava kot neodvisna spremenljivka do časa (t), kjer stalnica C vzemite vrednosti, ki definirajo začetni pogoji posebnega primera.

Če je vzet začetni primer: ∫ (2x+1) dx = x² + x + C

Veljaven začetni pogoj je lahko kondicioniranje grafike, ki jo je treba prehoditi skozi določeno koordinato. Na primer, znano je, da je primitiven (x² + x + C) Pojdite skozi točko (1, 2)

F (x) = x² + x + C; To je splošna rešitev

F (1) = 2

Splošno rešitev nadomestimo v tej enakosti

F (1) = (1)² + (1) + c = 2

Kjer je to enostavno sklepati C = 0

Na ta način je ustrezen primitiv za ta primer F (x) = x² + x

Obstajajo različne vrste numeričnih vaj, ki delujejo z Konstante integracije. Pravzaprav diferencialni in integralni računanje ne preneha uporabljati v trenutnih preiskavah. Na različnih akademskih ravneh lahko najdete; Od začetnega izračuna, s fiziko, kemijo, biologijo, gospodarstvom, med drugim.

Cenimo ga tudi pri študiji diferencialne enačbe, kje za Konstanta integracije To lahko vzamete različne vrednosti in rešitve, to zaradi več napotnic in integracij, ki se izvajajo v tej zadevi.

Primeri

Primer 1

1. Top, ki se nahaja 30 metrov visok poganjki navpično navzgor po izstrelku. Znano je, da je začetna hitrost izstrelka 25 m/s. Določiti:

• Funkcija, ki določa položaj projektila glede na čas.
• Čas leta ali čas, v katerem delček igra tla.

Lahko vam služi: 8 vrst napak v meritvah (s primeri)

Znano je, da je v enakomerno raznolikem rekvilinearnem gibanju pospešek konstantna vrednost. To je primer izstrelitve izstrelke, kjer bo pospešek gravitacija

G = - 10 m/s²

Znano je tudi, da je pospešek drugi izpeljan iz položaja, kar kaže na dvojno integracijo v ločljivost vaje in tako pridobi dve Konstante integracije.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Začetni pogoji vaje kažejo, da je začetna hitrost V₀ = 25 m/s. To je hitrost v času T = 0. Na ta način se izpolni:

V (0) = 25 = -10 (0) + C₁   in C₁ = 25

Funkcija hitrosti je opredeljena

V (t) = -10t + 25; Podobnost lahko vidite s formulo MRUV (V_F = V₀ + A x t)

V homolognem je funkcija hitrosti integrirana za dosego izraza, ki določa položaj:

R (t) = ∫v (t) dt = ∫ (-10t+25) dt = -5t² + 25T + C₂

R (t) = -5t² + 25T + C₂  (Primitivni položaj)

Začetni položaj r (0) = 30 m je znan. Potem se izračuna posebna primitiv izstrelitve.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Kje C₂ = 30

Prvi razdelek je reševan od R (t) = -5t² + 25T + 30  ; Ta izraz je homologn od formule premika v MRUV r (t) = r₀ + V₀T - gt²/2

Za drugi razdelek je treba rešiti kvadratno enačbo: -5T² + 25T + 30 = 0

Ker delca določa, da doseže tla (položaj = 0)

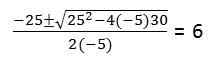Vir: Avtor

Pravzaprav enačba 2. razreda vrže 2 rešitvi T: 6, -1. Vrednost t = -1 se prezre, ker so to enote časa, katerih domena ne vključujejo negativnih številk.

Na ta način se reši drugi odsek, kjer je čas letenja enak 6 sekundah.

Primer 2

2. Poiščite primitivni f (x), ki izpolnjuje začetne pogoje:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Z informacijami o drugem izpeljanem izpeljanju f "(x) = 4 se začne postopek antiderivacije

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Potem, če poznam pogoj f '(2) = 2 izkupička:

4 (2) + c₁ = 2

C₁ = -6 in f '(x) = 4x - 8

Nadaljujte na enak način za drugo Konstanta integracije

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Začetni pogoj F (0) = 7 je znan in nadaljuje:

2 (0)² - 8 (0) + c₂ = 7

C₂ = 7 in f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Podobno kot v prejšnji težavi določimo prve derivate in prvotno funkcijo iz začetnih pogojev.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + c₁

S pogojem f '(0) = 6 prihodkov:

Vam lahko služi: teorija nastavitve: značilnosti, elementi, primeri, vaje

(0³/3) + c₁ = 6; Kje₁ = 6 in f '(x) = (x³/3) + 6

Potem drugo Konstanta integracije

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Začetni pogoj F (0) = 3 je znan in nadaljuje:

[(0)⁴/12] + 6 (0) + c₂ = 3; Kje₂ = 3

Dobimo posebno primitiv

f (x) = (x⁴/12) + 6x + 3

Primer 3

3. Določite primitivne funkcije glede na derivati ​​in točko grafa:

• dy/dx = 2x - 2, ki gre skozi točko (3, 2)

Pomembno si je zapomniti, da se derivati ​​nanašajo na naklon črte tangente na krivuljo v določeni točki. Kjer ni pravilno domnevati, da se grafika derivata dotakne navedene točke, saj spada v graf primitivne funkcije.

Na ta način izražamo diferencialno enačbo na naslednji način:

dy = (2x - 2) dx  ; Nato pri uporabi meril za antiderivacijo imate:

∫Dy = ∫ (2x - 2) dx

y = x² - 2x + c

Uporaba začetnega pogoja:

2 = (3)² - 2 (3) + c

C = -1

Je pridobljeno: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1, ki gre skozi točko (0, 2)

Diferencialno enačbo izražamo na naslednji način:

dy = (3x² - 1) dx  ; Nato pri uporabi meril za antiderivacijo imate:

 ∫Dy = ∫ (3x² - 1) dx

y = x³ - x + c

Uporaba začetnega pogoja:

2 = (0)² - 2 (0) + c

C = 2

Je pridobljeno: f (x) = x³ - x + 2

Predlagane vaje

Vaja 1

1. Poiščite primitivni f (x), ki izpolnjuje začetne pogoje:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Vaja 2

2. Balon, ki se dviga s 16 čevljev/s hitrostjo, sprosti peščeno jakno z višine 64 čevljev nad gladino tal.

• Določite čas letenja
• Kakšen bo vektor V_F Ko se dotaknete tal?

Vaja 3

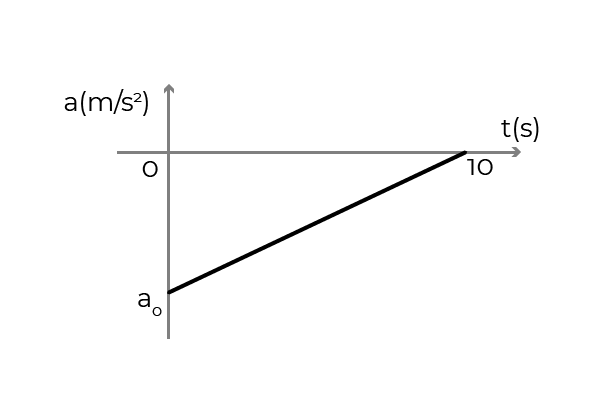
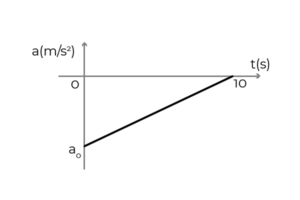
3. Slika prikazuje graf pospeška - čas avtomobila, ki se premika v pozitivnem pomenu osi x. Avto je potoval do konstantne hitrosti 54 km/h, ko je voznik v 10 sekundah nanesel zavore, da se ustavi. Določiti:

• Začetni pospešek avtomobila
• Hitrost avtomobila pri t = 5s
• Premik avtomobila med zaviranjem

Vir: Avtor

Vaja 4

4. Določite primitivne funkcije glede na derivati ​​in točko grafa:

• dy/dx = x, ki gre skozi točko (-1, 4)
• dy/dx = -x² + 1, ki gre skozi točko (0, 0)
• dy/dx = -x + 1, ki gre skozi točko (-2, 2)

Reference

1. Integralni računanje. Nedoločene integralne in integracijske metode. Wilson, Velásquez Bastidas. Univerza Magdalena 2014
2. Stewart, J. (2001). Izračun spremenljivke. Zgodnji transcendent. Mehika: Thomson Learning.
3. Jiménez, r. (2011). Matematika VI. Integralni računanje. Mehika: Pearson Education.
4. Fizika i. MC Graw Hill