Kongruentne številke, merila, primeri, vaje

The skladnost, V geometriji poudarja, da če imata dve ravni figure enako obliko in dimenzije, sta ta skladna. Na primer, dva segmenta sta skladna, kadar sta njihovi dolžini enaki. Tudi skladni koti imajo enak ukrep, čeprav v ravnini niso usmerjeni na enak način.

Izraz "skladnost" izvira iz latinščine Kongreentia, katere pomen je dopisovanje. Tako dve skladni številki ustrezata točno ena z drugim.

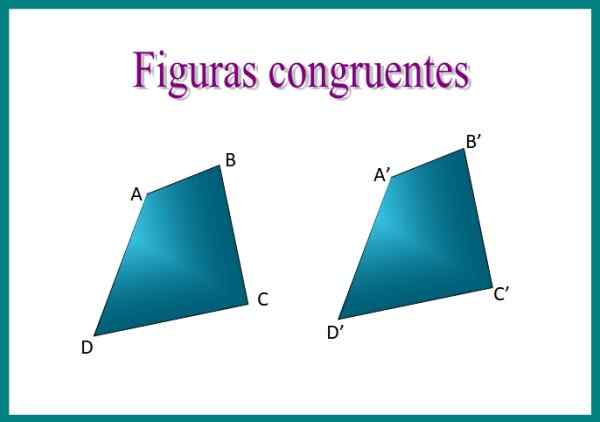
Slika 1. Quadrilateral ABCD in A'B'c'd 'figure sta skladni: njihove strani imajo enak ukrep, pa tudi njihove notranje kote. Vir: f. Zapata.

Na primer, če prekrivamo dva štirikolesnika slike, bomo ugotovili, da sta skladni, saj je razporeditev njihovih strani enaka in enaka merita isto.

Ko postavite štirikolesnike ABCD in A'B'c'd 'na drugo, bodo številke natančno sovpadale. Ujemajoče se strani se imenujejo homologne strani tudi ustrezno In za izražanje skladnosti se uporablja simbol ≡. Potem lahko rečemo, da je ABCD ≡ A'B'c'd '.

[TOC]

Merila za skladnost

Naslednje značilnosti so običajne za kongruentne poligone:

-Enaka oblika in velikost.

-Enaki ukrepi vaših kotov.

-V enakem obsegu na vsaki strani.

V primeru, da sta dva zadevna poligona redna, to je, da vse strani in notranji koti merijo enako, je skladnost zagotovljena, ko je izpolnjen eden od naslednjih pogojev:

-Strani so skladne

-The apoteme imajo isti ukrep

-On radio vsakega poligona meri enako

Apotema navadnega poligona je razdalja med sredino in eno od strani, polmer.

Merila za skladnost se pogosto uporabljajo, ker je veliko delov in kosov vseh vrst izdelanih zaporedno in morajo imeti enako obliko in ukrepe. Na ta način jih je mogoče enostavno zamenjati, kadar je to potrebno, na primer oreščki, vijaki, listi ali kamnine tal na ulici.

Lahko vam služi: pravilo Simpsona: formula, demonstracije, primeri, vajeSlika 2. Ulični kalbeni so skladne številke, saj sta njihova oblika in dimenzije popolnoma enaki, čeprav se njihova orientacija na tleh lahko spremeni. Vir: Pixabay.

Skladnost, identiteta in podobnost

Na primer obstajajo geometrijski koncepti, povezani s skladnostjo Enake številke in Podobne številke, ki ne pomenijo nujno, da so številke skladne.

Upoštevajte, da so skladne številke enake, vendar bi lahko četverice na sliki 1 na ravnino usmerili na različne načine in še vedno so skladne, saj različna orientacija ne spreminja velikosti svojih strani ali njihovih zornih kotov. V tem primeru bi prenehali biti enaki.

Drugi koncept je podobnost figur: dve ravni številki sta podobni, če imata enako obliko in njihovi notranji koti merijo enako, čeprav je velikost številk drugačna. V tem primeru številke niso skladne.

Primeri skladnosti

- Skladnost kotov

Kot smo na začetku navedli, imajo kongruentni koti enak ukrep. Obstaja več načinov za pridobitev skladnih kotov:

Primer 1

Dve vrstici s skupno točko določata dva kota, imenovana Nasproti kotov z vrhom. Ti koti imajo enak ukrep, zato so skladni.

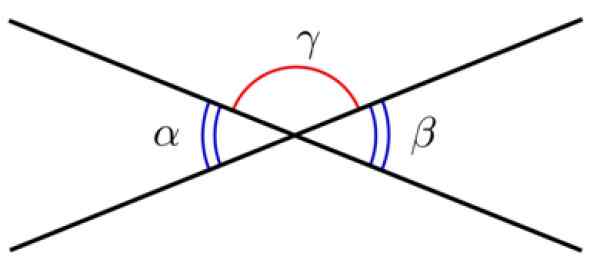Slika 3. Nasproti kotov z vrhom. Vir: Wikimedia Commons.

Primer 2

Obstajata dve vzporedni črti in črta t ki jih seka oba. Kot v prejšnjem primeru, ko ta črta seka vzporednice, ustvarja kongresne kote, po enega na vsaki črti na desni strani in še dva na levi strani. Slika prikazuje α in α₁, desno od črte t, So skladni.

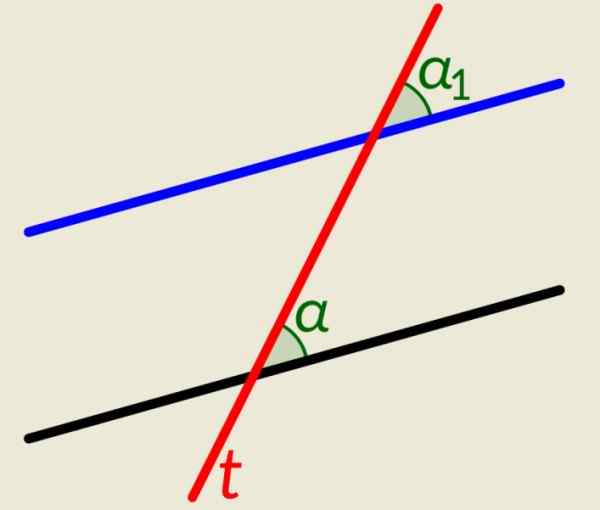Slika 4. Koti, prikazani na sliki, so skladni. Vir: Wikimedia Commons. Lfahlberg/cc by-sa (https: // creativeCommons.Org/licence/by-sa/3.0.

Primer 3

V paralelogramu so štirje notranji koti, ki so skladni dve do dva. So tisti med nasprotnimi tonicama, kot je prikazano na naslednji sliki, v katerih sta oba zelena kota skladna, pa tudi dva kota v rdeči barvi.

Vam lahko služi: akutantni trikotnik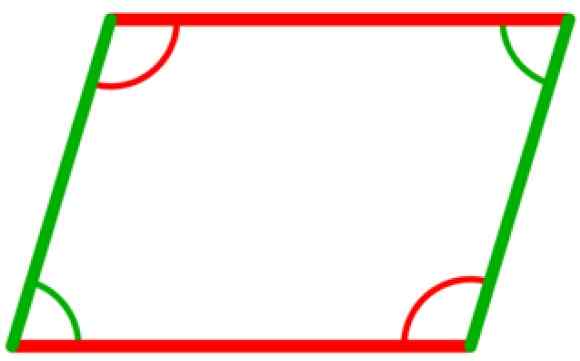Slika 5. Notranji koti paralelograma so skladni dve do dva. Vir: Wikimedia Commons.

- Skladnost trikotnikov

Dva trikotnika enake oblike in enake velikosti sta skladni. Če želite to preveriti, obstajajo tri merila, ki jih je mogoče pregledati v iskanju skladnosti:

-Merila LLL: Tri strani trikotnikov imajo enake ukrepe, torej l₁ = L '₁; L₂ = L '₂ in l₃ = L '_3.

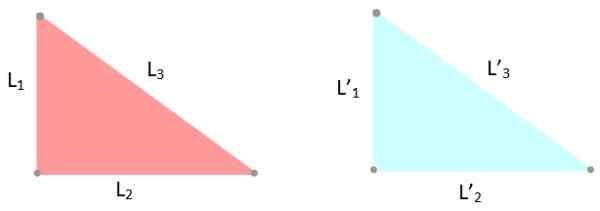Slika 6. Primer skladnih trikotnikov, katerih strani merijo enako. Vir: f. Zapata.

-Merila alla y aal: Trikotniki imajo dva enaka notranja kota in stran med temi koti ima enak ukrep.

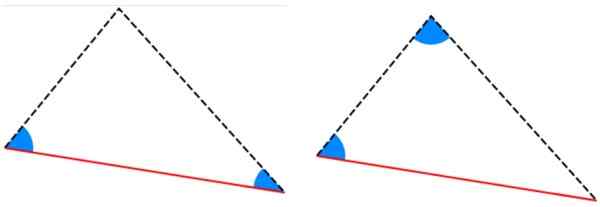Slika 7. Merila Ala in AAL za skladnost trikotnikov. Vir: Wikimedia Commons.

-Merila LAL: Dve strani sta enaki (ustrezni) in med njimi je enak kot.

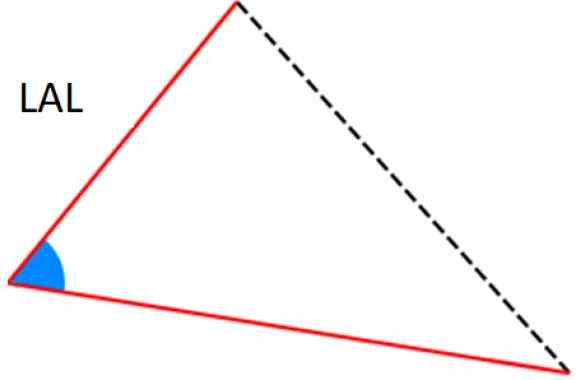Slika 8. LAL merila za skladnost trikotnikov. Vir: Wikimedia Commons.

Rešene vaje

- Vaja 1

Na naslednji sliki sta prikazana dva trikotnika: ΔABC in ΔECF. Znano je, da AC = EF, da AB = 6 in da CF = 10. Poleg tega sta kota ∡Bac in ∡fec skladna, kota ∡acb in ∡fcb pa sta tudi.

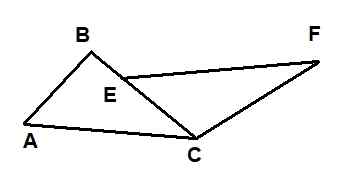Slika 9. Trikotniki za primer razrešeni 1. Vir: f. Zapata.

Potem je dolžina segmenta enaka:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Rešitev

Ker imata oba trikotnika ena stran enake dolžine AC = EF med enakimi koti ∡Bac = ∡cef in ∡BCA = ∡cfe, lahko rečemo, da sta oba trikotnika skladna po kriterijih kriterij.

To je ΔBAC ≡ ΔCEF, zato morate:

Ba = ce = ab = 6

Bc = cf = 10

Ac = ef

Toda segment, ki ga želite izračunati, je = BC - EC = 10 - 6 = 4.

Tako da je pravilen odgovor (iii).

- Vaja 2

Na sliki so prikazani trije trikotniki. Znano je tudi, da oba navedena kota merita 80 ° in da segmenti ab = pd in AP = cd. Poiščite vrednost kota x, prikazano na sliki.

Lahko vam služi: polibalna grafika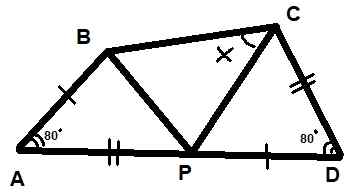Slika 10. Trikotniki za primer rešeni 2. Vir: f. Zapata.

Rešitev

Uporabiti morate lastnosti trikotnikov, ki so podrobno opisane korak za korakom.

Korak 1

Začenši z merili za skladnost Lal Triangles, lahko rečemo, da sta trikotniki BAP in PDC skladni:

ΔBAP ≡ Δpdc

2. korak

Zgornje vodi do potrditve, da je BP = PC, zato je trikotnik ΔBPC izosceles in ∡pcb = ∡pbc = x.

Korak 3

Če pokličemo γ pod kotom BPC, sledi:

2x + γ = 180 °

4. korak

In če pokličemo β na kote APB in DCP ter α na kote ABP in DPC, mora:

α + β + γ = 180 ° (ker je APB raven kot).

5. korak

Poleg tega α + β + 80 ° = 180 ° vsoto notranjih kotov APB trikotnika.

6. korak

Če združite vse te izraze, morate:

α + β = 100 °

7. korak

In zato:

γ = 80 °.

Korak 8

Končno sledi, da:

2x + 80 ° = 180 °

Z x = 50 °.

Reference

1. Baldor, a. 1973.Ravna in vesoljska geometrija. Srednjeameriška kulturna.
2. Fundacija CK-12. Skladni poligoni. Pridobljeno iz: CK 12.org.
3. Uživajte v matematiki. Opredelitve: radio (poligon). Okrevano od: Uživajte.com.
4. Open Reference Math Open. Testiranje poligonov za kongruence. Okreval od: Mathpenref.com.
5. Wikipedija. Skladnost (geometrija). Okrevano od: je.Wikipedija.org.
6. Zapata, f. Trikotniki, zgodovina, elementi, klasifikacija, lastnosti. Pridobljeno iz: Lifer.com.