Pravokotne sestavine vektorja (z vajami)

The pravokotne komponente vektorja so podatki, ki sestavljajo ta vektor. Če jih želite določiti, je treba imeti koordinatni sistem, ki je običajno kartezijanska ravnina.

Ko imate vektor v koordinatnem sistemu, lahko njegove komponente izračunate. To sta 2, vodoravna komponenta (vzporedna z osi x), imenovana "komponenta v osi x", in navpična komponenta (vzporedno z osi y), imenovana "komponenta v osi y".

Grafični prikaz pravokotnih komponent vektorja

Za določitev komponent je potrebno.

[TOC]

Kako določiti pravokotne komponente vektorja?

Za določitev teh komponent je treba poznati določena razmerja med pravokotniki in trigonometričnimi funkcijami.

Na naslednji sliki si lahko ogledate to razmerje.

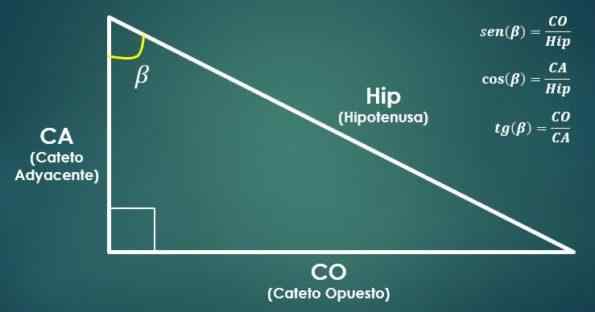Razmerja med pravokotniki in trigonometričnimi funkcijami

Natiček kota je enak količniku med mero kateta, ki nasprotuje kotu in mero hipotenuze.

Po drugi strani je kosinus kota enak količniku med mero kateta, ki meji na kota, in mero hipotenuze.

Tangenta kota je enaka količnik med mero nasprotne noge in mero sosednjega kateta.

V vseh teh odnosih je treba vzpostaviti ustrezen trikotnik pravokotnika.

Ali obstajajo druge metode?

Ja. Odvisno od predloženih podatkov se lahko način izračuna pravokotnih komponent vektorja spreminja. Drugo orodje, ki se veliko uporablja, je teorem Pythagoras.

Vam lahko služi: Teorem o obstoju in edinstvenosti: demonstracija, primeri in vaje

Rešene vaje

Naslednje vaje v praksi opredelijo pravokotne sestavine vektorja in zgoraj opisanih odnosov.

Prva vaja

Znano je, da ima vektor A velikost, enaka 12, in kot, da ima ta oblika z osi x 30 °. Določite pravokotne komponente omenjenega vektorja.

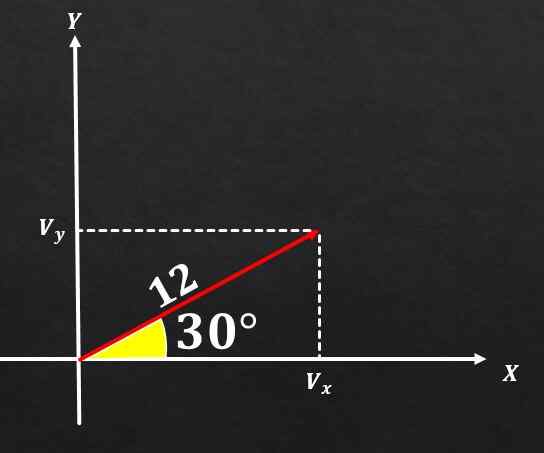
Rešitev

Če je slika cenjena in uporabljena zgoraj opisana formule, je mogoče sklepati, da je komponenta v vektorju A enaka

sin (30 °) = vy / 12, zato Vy = 12*(1/2) = 6.

Po drugi strani je komponenta na osi x vektorja A enaka

cos (30 °) = vx / 12 in zato vx = 12*(√3 / 2) = 6√3.

Druga vaja

Če ima vektor A velikost, enaka 5 in je komponenta na osi x enaka 4, določite vrednost komponente na osi y.

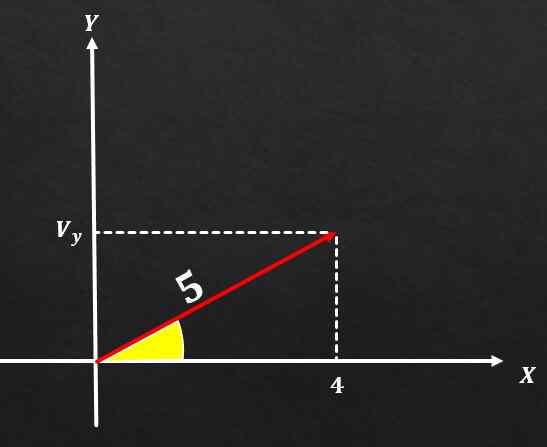
Rešitev

Z uporabo teorema Pitagore je velikost vektorja A visok kvadrat enaka vsoti kvadratov obeh pravokotnih komponent. To pomeni, da m² = (vx) ² + (Vy) ².

Zamenjava zagotovljenih vrednosti morate

5² = (4) ² + (Vy) ², torej 25 = 16 + (Vy) ².

To pomeni, da (Vy) ² = 9 in posledično Vy = 3.

Tretja vaja

Če ima vektor A velikost, enaka 4 in ta tvori kot 45 ° z osi X, določite pravokotne komponente omenjenega vektorja.

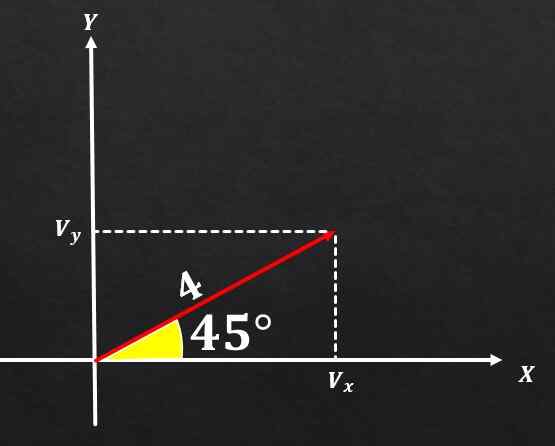
Rešitev

Z uporabo odnosov med pravokotnim trikotnikom in trigonometričnimi funkcijami je mogoče sklepati, da je komponenta na in vektorju A enaka

sin (45 °) = vy / 4 in zato Vy = 4*(√2 / 2) = 2√2.

Po drugi strani je komponenta na osi x vektorja A enaka

Vam lahko služi: sestavljeno nasledstvo

cos (45 °) = vx / 4 in zato vx = 4*(√2 / 2) = 2√2.

Reference

1. Landaverde, f. D. (1997). Geometrija (Ponatis ed.). Napredek.
2. Leake, d. (2006). Trikotniki (Illustrated Ed.). Heinemann-raintree.
3. Pérez, c. D. (2006). Prekalenkulacija. Pearson Education.
4. Ruiz, Á., & Barrantes, h. (2006). Geometrije. CR tehnološka.
5. Sullivan, m. (1997). Prekalenkulacija. Pearson Education.
6. Sullivan, m. (1997). Trigonometrija in analitična geometrija. Pearson Education.