Kako dobiti kot trikotnika? (Primer)

Obstajajo različni načini Izračunajte stranice in kote trikotnika. Ti so odvisni od vrste trikotnika, s katerim delate.

Ob tej priložnosti bo prikazano, kako izračunati stranice in kote desnega trikotnika, ob predpostavki, da so določeni podatki o trikotniku s znanci z znanci.

Elementi, ki bodo uporabljeni, so:

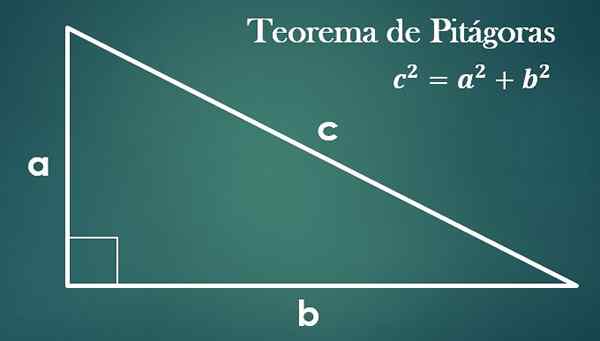
- Teorem za pitagore

Glede na pravokotnik trikotnik z "a", "b" in hipotenusa "c", je res, da je "c² = a²+b²".

- Območje trikotnika

Formula za izračun območja katerega koli trikotnika je A = (B × H)/2, kjer je "B" dolžina podstavka in "H" dolžina višine.

- Koti trikotnika

Vsota treh notranjih kotov trikotnika je 180 °.

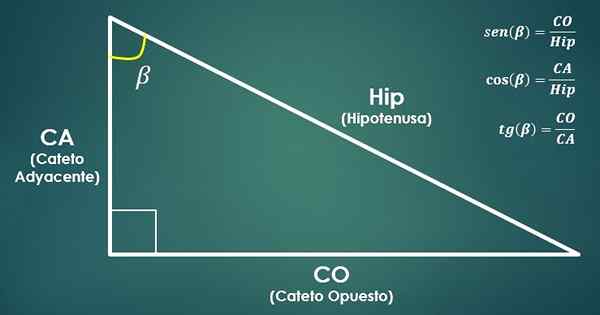
- Trigonometrične funkcije:

Razmislite o pravem trikotniku. Nato so trigonometrične funkcije definirani sinus, kosinus in tangent beta kota (β) na naslednji način:

sin (β) = co/hyp, cos (β) = ca/kolk in tan (β) = co/ca.

Kako izračunati strani in kote desnega trikotnika?

Glede na trikotnik ABC pravokotnika je mogoče predstaviti naslednje situacije:

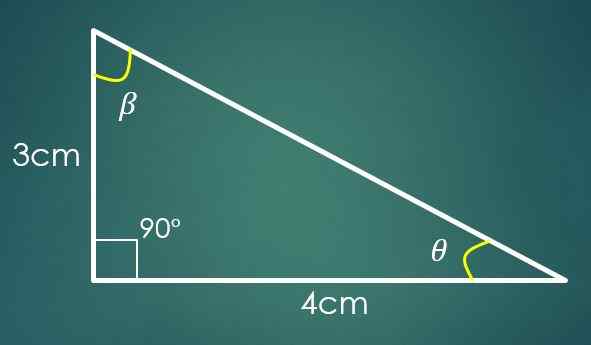
1- Obe nogi sta znani

Če Cateto "A" meri 3 cm in Cateto "B" meri 4 cm. Z zamenjavo vrednosti "a" in "b" se pridobi, da c² = 25 cm², kar pomeni, da je c = 5 cm.

Zdaj, če je kot β nasproten kategoriji "B", potem sin (β) = 4/5. Pri uporabi obratne funkcije dojke v tej zadnji enakosti dobimo, da je β = 53,13 °. Dva notranja kota trikotnika sta že znana.

Naj bo θ kot, ki ga je treba še poznati, nato 90 °+53,13 °+θ = 180 °, kjer dobimo, da je θ = 36,87 °.

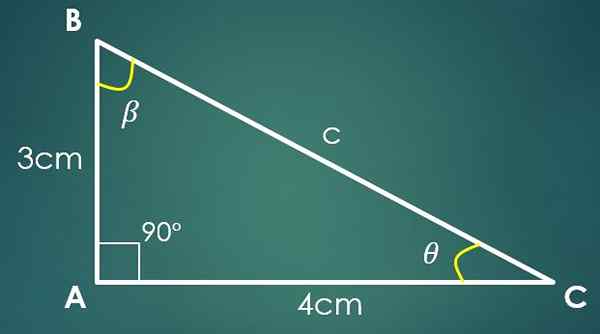
V tem primeru ni treba, da sta znani strani dve nogi, pomembno je vedeti vrednost katere koli dve strani.

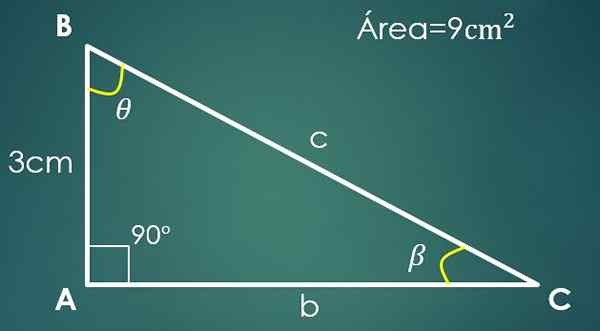
2- noga in območje je znano

Naj a = 3 cm znana noga in 9 cm² območje trikotnika.

V trikotniku pravokotnika se lahko kategorija šteje za osnovno, drugo pa kot višino (saj so pravokotne).

Recimo, da je "a" osnova, torej 9 = (3 × h)/2, kjer je pridobljeno, da druga kategorija meri 6 cm. Za izračun hipotenuze nadaljujte kot v prejšnjem primeru, in pridobljeno je, da je c = √45 cm.

Zdaj, če je kot β nasprotno s kateto "A", potem sin (β) = 3/√45. Pri čiščenju β je ugotovljeno, da je njegova vrednost 26,57 °. Samo vedeti morate vrednost tretjega kota θ.

Izpolnjeno je, da je 90 °+26,57 °+θ = 180 °, kjer je sklenjeno, da je θ = 63,43 °.

3- znan je kot in cateto

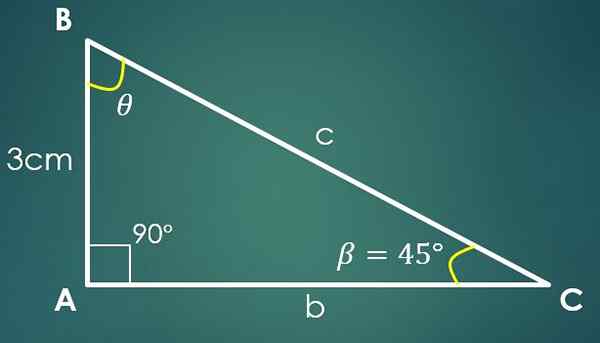
Naj β = 45 ° Znani kot in A = 3 cm znana noga, kjer je kateto "a" nasprotoval kot β. Z uporabo tangentne formule je pridobljeno, da je tg (45 °) = 3/ca, kjer se izkaže, da ca = 3 cm.

Z uporabo teorema Pythagora je pridobljeno, da je c² = 18 cm², torej c = 3√2 cm.

Znano je, da kota meri 90 ° in da β meri 45 °, od tu je sklenjeno, da tretji kot meri 45 °.

V tem primeru znane strani ni treba biti noga, lahko je katera od treh strani trikotnika.