Carnotove faze cikla, aplikacije, primeri, vaje

On Carnotov cikel Zaporedje termodinamičnih procesov poteka v Carnotovem motorju, idealni napravi, ki je sestavljena le iz reverzibilnih procesov; torej tisti, ki se lahko, ki so se zgodili, vrnejo v začetno stanje.

Ta vrsta motorja se šteje za idealno, saj mu primanjkuje disipacije, trenja ali viskoznosti, ki nastanejo v resničnih strojih, kar toplotno energijo spremeni v uporabno delo, čeprav se pretvorba ne izvaja 100%.

Slika 1. Parna lokomotiva. Vir: Pixabay

Motor je zgrajen na podlagi snovi, ki lahko opravlja delo, kot so plin, bencin ali para. Ta snov je podvržena različnim temperaturnim spremembam in posledično doživlja spremembe v njegovem tlaku in prostornini. Na ta način je mogoče premikati bat znotraj valja.

[TOC]

Kakšen je Carnotov cikel?

Carnotov cikel poteka znotraj sistema, imenovanega motorja Carnot ali C, ki je idealen plin, zaklenjen v valj in je opremljen z batom, ki je v stiku z dvema virima pri različnih temperaturah t₁ in t₂ kot tista, prikazana na naslednji sliki na levi strani.

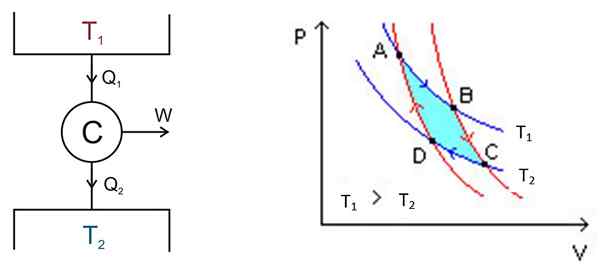Slika 2. Na levi shemi stroja C arnot na desni strani PV diagram. Vir leve številke: Keta - lastno delo, CC do 2.5, https: // commons.Wikimedia.org/w/indeks.Php?Curid = 681753, desna številka Wikimedia Commons.

V grobem načinu obstajajo naslednji procesi:

1. Napravi je na voljo določena količina toplote_vhod = Q₁ Iz toplotnega rezervoarja pri visoki temperaturi t₁.
2. Engine Carnot C opravi delo w zahvaljujoč tej vročini.
3. Del uporabljene toplote: odpadki q_izhod, Prenese se v toplotni rezervoar, ki je pri nižji temperaturi t₂.

Carnot cikla

Analiza je narejena s p -v diagramom (tlak -volume), kot je prikazano na sliki 2 (desna slika). Cilj motorja je lahko ohraniti toplotno deponiranje 2 mraza in iz njega pridobiva toploto. V tem primeru je Stroj za hladilno sredstvo. Če nasprotno, želite toploto dati toplotni nahajališču 1, potem je to Toplotna črpalka.

Diagram P -V prikazuje spremembe tlaka - temperatura motorja pod dvema pogojem:

- Vzdrževanje konstantne temperature (izotermalni postopek).

- Brez prenosa toplote (toplotna izolacija).

Dva izotermalna procesa je treba povezati, kar dosežemo s toplotno izolacijo.

Točka

Lahko začnete na kateri koli točki cikla, v katerem ima plin določene tlačne, volumske in temperaturne pogoje. Plin trpi vrsto procesov in se lahko vrne v začetne pogoje, da začne drug cikel, in vedno je končna notranja energija enaka začetnici. Ker je energija ohranjena:

Delo, ki ga opravi C = vhodna toplota - odhodna toplota

ΔW = q_vhod - Q_izhod

Območje, ki je vključeno v ta cikel ali zanko, v turkizi na sliki, je ravno enako delu, ki ga je opravil Carnot Engine.

Točke A, B, C in D so označene na sliki 2. Začelo se bo do sledenja modri puščici.

Prva faza: izotermalna širitev

Temperatura med točkami A in B je t₁. Sistem absorbira toploto iz toplotnega nahajališča 1 in trpi izotermalno širitev. Nato se količina poveča in tlak se zniža.

Vendar temperatura ostane v t₁, Ker ko se plin razširi, se ohladi. Zato njegova notranja energija ostane konstantna.

Lahko vam služi: Graff Van Generator: zabave, kako deluje, aplikacije

Druga stopnja: adiabatska širitev

V točki B sistem začne novo širitev, v kateri sistem ne zmaga ali izgubi toplote. To dosežemo tako, da ga damo v kalorično izolacijo, kot je navedeno prej. Zato gre za adiabatsko širitev, ki še naprej kaže C po rdeči puščici. Količina se poveča in tlak se zniža, dokler ne doseže najnižje vrednosti.

Tretja faza: izotermalno stiskanje

Začnite v točki C in končajte v D. Izolacija se odstrani in sistem pride v stik s toplotnim nahajališčem 2, katerega temperatura t₂ Manj je. Sistem daje odpadno toploto na toplotni rezervoar, tlak se začne povečevati in prostornina se zmanjšuje.

Četrta faza: adiabatsko stiskanje

Dosežen do točke D, sistem se vrne na toplotno izolacijo, tlak se poveča in volumen se zmanjšuje, dokler ne dosežejo prvotnih pogojev točke A. Potem se cikel znova ponovi.

Carnotov teorem

Carnotovega teorema je na začetku 19. stoletja prvič postavil francoski fizik Sadi Carnot. Leta 1824 je Carnot, ki je bil del francoske vojske, objavil knjigo, v kateri je predlagal odgovor na naslednje vprašanje: Pod kakšnimi pogoji ima toplotni stroj največjo učinkovitost? Carnot je nato vzpostavil naslednje:

Noben toplotni motor, ki deluje med dvema toplotnima nahajališčih, ni učinkovitejši od Carnotovega motorja.

Η izkoristek toplotnega motorja je dano z razmerjem med opravljenim delom W in absorbirano toploto Q:

uspešnost = opravljeno delo/toploto absorbira

Na ta način je zmogljivost katerega koli toplotnega motorja I: η = w/q. Medtem ko je zmogljivost motorja Carnot R η '= w/q', lahko v primeru obeh motorjev opravljajo isto delo.

Carnotov teorem navaja, da η nikoli ni večji od η '. V nasprotnem primeru spada v protislovje z drugim zakonom termodinamike, v skladu s tem, v katerem je postopek, v katerem je to toplota iz telesa nižje temperature, ni mogoče iti na drugo višjo temperaturo, ne da bi prejeli zunanjo pomoč. Zato:

η _< η^'

Carnotova teoremska demonstracija

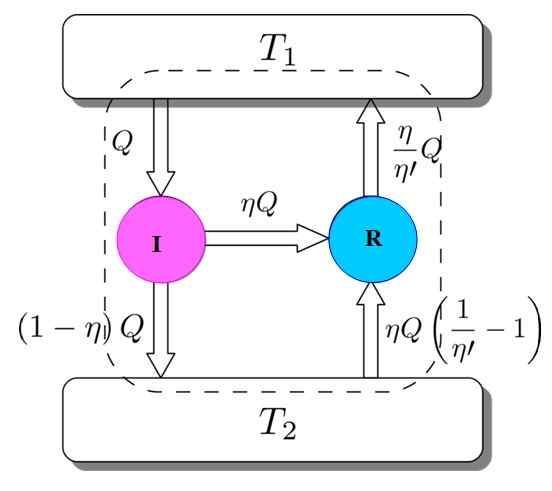
Če želite pokazati, da je temu tako, razmislite o Carnotovem motorju, ki deluje kot hladilni stroj, ki ga poganja I motor. To je mogoče, saj Carnot Engine deluje z reverzibilnimi procesi, kot je določeno na začetku.

Slika 3. Carnotova teoremska demonstracija. Vir: Netheril96 [CC BY-SA 3.0 (https: // creativeCommons.Org/licence/by-sa/3.0)]

Imate oboje: jaz in r delata z istimi toplotnimi nahajališči in domnevamo, da η _> η^'. Če se na poti doseže protislovje z drugim zakonom termodinamike, se Carnotov teorem dokaže z zmanjšanjem na nesmiselnost.

Slika 3 pomaga slediti postopku. I motor I vzame količino toplote q, ki se na ta način razdeli: opravljanje dela na r, ki ustreza W = ηq, preostali₂.

Ker je energija ohranjena, se vse izpolni:

In_vhod = Q = delo w + toplota, dodeljena t₂ = ηq + (1 -η) q = e_izhod

Zdaj hladilni stroj Carnot R vzame toplotno rezervoar 2 količino toplote, ki jo daje:

Lahko vam služi: IMANTATION: Kaj je sestavljeno, metoda in primeri

(η / η ') (1 -η') q =

V tem primeru je treba hraniti tudi energijo:

In_vhod = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_izhod

Rezultat je prenos na toplotni rezervoar t₂ količine toplote, ki jo daje (η / η ') Q = Q'.

Če je η večji od η ', to pomeni, da je najvišja temperaturna toplotna nahajališče prišlo več toplote, kot sem prvotno vzel. Ker ni sodeloval noben zunanji agent, kot je še en toplotni vir.

To se ne strinja z drugim zakonom termodinamike. Takrat je sklenjeno, da ni mogoče, da η^' Biti manj kot η, zato I motor ne more imeti več zmogljivosti kot stroj Carnot R.

Teorem in omejitve

Carnotov teorem Corellary pravi, da imata dva Carnotova stroja enako učinkovitost, če oba delujeta z enakimi toplotnimi nahajališči.

To pomeni, da snov ni pomembna, uspešnost je neodvisna in je ni mogoče dvigniti s spreminjanjem.

Zaključek prejšnje analize je, da je Carnotov cikel vrh idealno dosegljivega termodinamičnega procesa. V praksi obstaja veliko dejavnikov, ki zmanjšujejo učinkovitost, na primer dejstvo, da izolacija ni nikoli popolna in v adiabatskih fazah dejansko obstaja kalorična izmenjava z zunanjostjo.

V primeru avtomobila se blok motorja segreje. Po drugi strani se mešanica za plin in zrak ne obnaša točno kot idealen plin, ki je izhodišče Carnotovega cikla. To omenja le nekaj dejavnikov, ki bodo povzročili drastično zmanjšanje zmogljivosti.

Primeri

Bat znotraj valja

Če je sistem bat, zaklenjen v valj, kot je na sliki 4, se bat dvigne med izotermalno širitvijo, kot je razvidno iz prve sheme skrajne levice in se tudi med adiabatsko ekspanzijo dvigne.

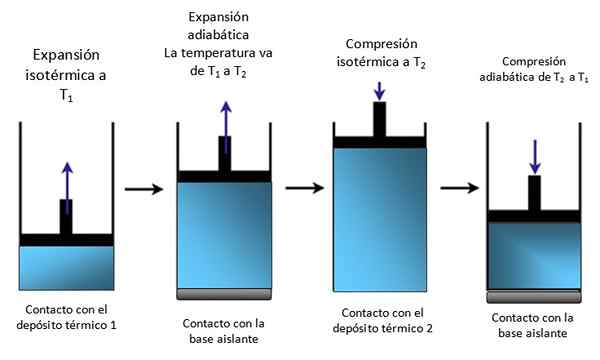Slika 4. Gibanje bata znotraj valja. Vir: Self Made.

Nato izotermično stisnjeni, dajejo toploto in se še naprej adiabatno stisne. Rezultat je gibanje, v katerem se bat dviga in navzdol znotraj valja in se lahko na primer prenaša na druge dele določene naprave, na primer avtomobilski motor, ki proizvaja par, ali parni stroj.

Različni reverzibilni procesi

Poleg širitve in stiskanja idealnega plina znotraj valja obstajajo tudi drugi idealni reverzibilni procesi, s katerimi je mogoče konfigurirati Carnotov cikel:

- Okrogla gibanja potovanja v odsotnosti trenja.

- Idealna vzmet, ki je stisnjena in dekompresirana in to nikoli ni deformirano.

- Električna vezja, v katerih ni upora, ki bi razpršila energijo.

- Cikli magnetizacije in demagnetizacije, v katerih ni izgub.

- Nalaganje in nalaganje baterije.

Jedrska elektrarna

Čeprav gre za zelo zapleten sistem, je prvi pristop tistega, kar je potrebno za proizvodnjo energije v jedrskem reaktorju, tisti, ki sledi:

- Toplotni vir, sestavljen iz materiala, ki se radioaktivno razgradi kot uran.

Vam lahko služi: trenutni atomski model

- Umivalnik ali hladno toplotno nahajališče, ki bi bilo vzdušje.

- "Carnotov stroj", ki uporablja tekočino, skoraj vedno tekočo vodo, ki se dobavlja toplota iz toplotnega vira, da jo spremeni v paro.

Ko se cikel izvaja, se elektrika pridobi kot neto delo. Ko se pretvori v visoko temperaturno paro, se voda doseže do turbine, kjer se energija pretvori v gibanje ali kinetično energijo.

Turbina posledično aktivira električni generator, ki energijo gibanja pretvori v električno energijo. Poleg perečega materiala, kot je uran, se lahko seveda uporabijo fosilna goriva kot vir toplote.

Rešene vaje

-Primer 1: Učinkovitost toplotnega stroja

Učinkovitost toplotnega stroja je opredeljena kot razmerje med izhodnim delom in vhodnim delom, zato je brezdimenzionalna količina:

Največja učinkovitost = (q_vhod - Q _izhod) /Q_vhod

Označevanje največje učinkovitosti kot e_Max, Možno je pokazati njeno temperaturno odvisnost, ki je najlažja spremenljivka za merjenje, na primer:

in_Max = 1 - (t₂/T₁)

Kjer t₂ Je temperatura umivalnika in t₁ To je temperatura toplotnega vira. Ker je slednje večje, se učinkovitost vedno izkaže za manj kot 1.

Recimo, da lahko toplotni stroj dela na naslednjih načinih: a) med 200 K in 400 K, b) med 600 K in 400 K. Kakšna je učinkovitost v vsakem primeru?

Rešitev

a) V prvem primeru je učinkovitost:

in_Max1 = 1 - (200/400) = 0.petdeset

b) Za drugi način bo učinkovitost:

in_Max2 = 1- (400/600) = 0.33

Čeprav je temperaturna razlika enaka med obema načinama, učinkovitost ni. In še bolj opazno je, da najučinkovitejši način deluje pri nižji temperaturi.

-Primer 2: absorbirana toplota in prenehana toplota

22 -odstotni toplotni stroj proizvede 1530 j dela. Poiščite: a) Količina toplote, absorbirane iz toplotnega nahajališča 1, b) Količina toplote, zavržene na toplotno rezervoar 2.

a) V tem primeru se uporablja opredelitev učinkovitosti, saj je opravljeno delo, ne temperature toplotnih nahajališč. 22 -odstotna učinkovitost pomeni, da E _Max = 0.22, torej:

Največja učinkovitost = delo /q_vhod

Količina absorbirane toplote je natančno Q_vhod, Torej čiščenje imate:

Q_vhod = Delo/učinkovitost = 1530 j/0.22 = 6954.5 J

b) Količina toplote, dodeljene najhladnejšim rezervoarjemW = q_vhod - Q_izhod

Q_izhod = Q_vhod - ΔW = 6954.5 -1530 j = 5424.5 J.

Druga pot je od in_Max = 1 - (t₂/T₁). Ker temperature niso znane, vendar so te povezane s toploto, se lahko učinkovitost izraža tudi kot:

in_Max = 1 - (q_Sceding/Q_absorbira)

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 654-657
2. Nuklearna energija. Delovanje jedrske elektrarne. Okrevano od: energijsko jedrsko.mreža
3. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje. 618-622.
4. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 414-416.
5. Walker, J.2008. Fizika. 4. izd.Addison Wesley. 610-630