Domača stran
Fizično
Elastični pretresi v dimenziji, posebnih primerih, vajah

Fizično

Elastični pretresi v dimenziji, posebnih primerih, vajah

4425
794
Barry Ernser

The Elastični pretresi o Elastični trki so sestavljeni iz kratkih, a intenzivnih interakcij med predmeti, v katerih se ohranijo tako gibanje kot kinetično energijo. Choques so v naravi zelo pogosti dogodki: od subatomskih delcev do galaksij, ki gredo skozi biljardne kroglice in udarne avtomobile v atrakcijskih parkih, vsi so predmeti, ki se lahko trčijo.

Med trkom ali šokom so sile interakcije med predmeti zelo intenzivne, veliko več kot tisti, ki lahko delujejo zunaj. Na ta način je mogoče potrditi, da med trkom delci tvorijo izoliran sistem.

Trke med biljardnimi kroglicami se lahko štejejo za elastične. Vir: Pixabay.

V tem primeru se izpolni:

$\vecF_ext=\frac\mathrmd \vecP\mathrmd t=\vec0$ Kje Str To je vektorska količina gibanja, katerega velikost je MV (Hitrostna masa). Če derivat Str je ničelno, to pomeni Str To je konstantno. In to pomeni, da se ne razlikuje, da je ohranjen. Zato lahko potrdimo, da:

Str_tudi = P_F

Količina gibanja Str_tudi Pred trkom je enako kot po trku. To je izpolnjeno za kakršno koli trčenje, tako elastično kot neelastično.

Zdaj morate upoštevati naslednje: Med trkom objekti doživijo določeno deformacijo. Ko je spopad elastičen, predmeti hitro povrnejo prvotno obliko.

[TOC]

Ohranjanje kinetične energije

Običajno med šokom del energije predmetov porabimo za toploto, deformacijo, zvok in včasih tudi pri ustvarjanju svetlobe. Torej je kinetična energija sistema po trčenju manjša od prvotne kinetične energije.

Ko je kinetična energija k, se nato ohrani:

K_tudi = K_F

Kar pomeni, da so sile, ki delujejo med trkom. Medtem ko trčenje traja, se kinetična energija na kratko spremeni v potencialno energijo, potem pa je spet kinetična energija. Ustrezne kinetične energije se razlikujejo, vendar vsota ostane konstantna.

Popolnoma elastični trki niso pogosti, čeprav so biljardne kroglice dokaj dober pristop, pa tudi trki, ki potekajo med idealnimi molekulami gaze.

Elastični pretresi v dimenziji

Preučimo trk dveh delcev tega v eni dimenziji; To pomeni, da delci, ki se medsebojno premikajo, recimo, vzdolž osi x. Recimo, da imajo maso m₁ in m₂. Začetne hitrosti vsake so ali₁ in ali₂ oziroma. Končne hitrosti so v₁ in v₂.

Brez vektorja lahko to storimo, saj se gibanje izvaja vzdolž osi x, vendar znaka (-) in (+) kažeta na pomen gibanja. Na levi je negativen in na pozitivno desno, s konvencijo.

Vam lahko služi: Bravais Networks: koncept, značilnosti, primeri, vaje

-Formule za elastične trke

Za količino gibanja

m₁ali₁ + m₂ali₂ = m₁v₁ + m₂v₂

Za kinetično energijo

½ m₁ali²₁ + ½ m₂ali²₂ = ½ m₁v²₁ + ½ m₂v²₂

Kadar koli so znane začetne mase in hitrosti, je mogoče preusmeriti enačbe, da bi našli končne hitrosti.

Težava je v tem, da je načeloma potrebno. Ideal bi bil najti izraze, ki jih ne vsebujejo.

Prvi je, da brez faktorja ½ in preuredite obe enačbi tako, da se pojavi negativni znak in je lahko masa dejavnik:

m₁ali₁ - m₁v₁ = M₂v₂- m₂ali₂

m₁ali²₁ - m₁v²₁ = +M₂v²₂ - m₂ali²₂

Je izražen na ta način:

m₁(ali₁ - v₁ ) = m₂(v₂- ali₂)

m₁(ali²₁ - v²₁ ) = m₂(v²₂ - ali²₂)

Poenostavitev za odpravo kvadratov iz hitrosti

Zdaj morate uporabiti pomemben izdelek, dodaja svojo razliko v drugi enačbi, ki dobi izraz, ki ne vsebuje kvadratov, kot je bilo prvotno želeno:

m₁(ali₁ - v₁ ) = m₂(v₂- ali₂)

m₁(ali₁ - v₁ ) (ali₁ + v₁ ) = m₂(v₂ - ali₂) (v₂ + ali₂)

Naslednji korak je nadomestiti prvo enačbo v drugem:

m₂(v₂- ali₂) (ali₁ + v₁ ) = m₂(v₂ - ali₂) (v₂ + ali₂)

In ko se izraz ponovi m₂(v₂- ali₂) Na obeh straneh enakosti je ta izraz preklican in je tak:

(ali₁ + v₁) = (V₂ + ali₂)

Ali še bolje:

ali₁ - ali₂= v₂- v₁

Končne hitrosti v₁ in v₂ delcev

Zdaj obstajata dve linearni enačbi, s katerimi je lažje delati. Ponovno jih bomo postavili pod drugo:

m₁ali₁ + m₂ali₂ = m₁v₁ + m₂v₂

ali₁ - ali₂= v₂- v₁

Pomnožiti drugo enačbo m₁ In dodajanje izraza v izraz ostaja:

m₁ali₁ + m₂ali₂ = m₁v₁ + m₂v₂

m₁ali₁ - m₁ali₂= m₁v₂- m₁ v₁

2 m₁ali₁+ (m₂ - m₁) ali₂ = (m₂ + m₁) v₂

In že je mogoče razčistiti v₂. Na primer:

$v_2=\frac2m_1m_2+m_1u_1+\fracm_2-m_1m_2+m_1u_2$ Podobno zdravljenje je mogoče storiti za iskanje enačbe za v₁. Bralec ostane kot vaja, da dokaže, da:

$v_1=\frac2m_2m_2+m_1u_2+\fracm_1-m_2m_2+m_1u_1$

Posebni primeri v elastičnih trkih

Zdaj, ko so na voljo enačbe za končne hitrosti obeh delcev, je čas, da analiziramo nekatere posebne situacije.

Dve enaki masi

Nato m₁ = m₂ = m in:

v₁= u₂

v₂= u₁

Delci preprosto izmenjujejo svoje hitrosti po trku.

Dve enaki masi, od katerih je bila ena sprva v mirovanju

Ponovno m₁ = m₂ = m in ob predpostavki ali₁ = 0:

v₁= u₂

v₂= 0

Po zrušitvi delček, ki je bil v mirovanju, pridobi enako hitrost delca, ki se je premikal, in se nato ustavi.

Vam lahko služi: hidravlični tlak

Dve različni masi, ena od njih sprva v mirovanju

V tem primeru predpostavimo ali₁ = 0, Toda množice so drugačne:

$v_1=\frac2m_2m_2+m_1u_2$ $v_2=\fracm_2-m_1m_2+m_1u_2$

Kaj če m₁ je veliko večji od m₂?

$v_1\approx 0$

$v_2\approx -u_2$

Zgodi se, da m₁ Bodite v mirovanju in m₂ Vrne se z enako hitrostjo, s katero je vplivala.

Huygens-Newton koeficient ali pravilo

Prej je bilo sklenjeno naslednje razmerje med hitrostmi za dva predmeta v elastičnem trku: ali₁ - ali₂= v₂- v₁. Te razlike so relativne hitrosti pred in po trčenju. Na splošno je za trčenje izpolnjeno:

ali₁ - ali₂= -(v₁- v₂)

Koncept relativne hitrosti je bolje ceniti, če bralec predstavlja, da je na enem od delcev in s tega položaja opazuje hitrost, s katero se premika drugi delček. Prejšnja enačba je napisana tako:

$\fracv_2-v_1u_1-u_2=1$ Če kinetična energija ni ohranjena, bo navedeni količnik manjši od 1. Pokličimo in na vrednost omenjenega količnika brezdimenzije:

$e=\fracv_2-v_1u_1-u_2$ O No:

$e=-\fracv_1-v_2u_1-u_2$ Vrednost in je med 0 in 1 in se imenuje Koeficient vračila. Ko je spopad elastičen, E = 1. Ko je popolnoma neelastična, E = 0, medtem ko ima kakšno drugo vmesno vrednost, se je neka kinetična energija razpršila v drugih vrstah energije.

Rešene vaje

-Vaja rešena 1

Žoga biljarda se premakne v levo pri 30 cm/s in trči od spredaj z drugo identično kroglico, ki se premakne desno na 20 cm/s. Obe krogli imata isto testo in trk je popolnoma elastičen. Poiščite hitrost vsake kroglice po udarcu.

Rešitev

ali₁ = -30 cm/s

ali₂ = +20 cm/s

To je poseben primer, da se v elastično dimenziji trčita dve enaki masi, zato se hitrosti izmenjujejo.

v₁ = +20 cm/s

v₂ = -30 cm/s

-Vaja Rešena 2

Koeficient restitucije žoge, ki odskoči na tleh, je enak 0,82. Če padete iz počitka, bo kakšen del originalne višine dosegel žogo, potem ko boste enkrat poskočili? In po treh skokih?

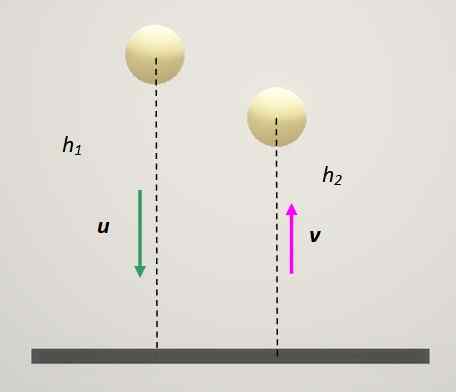Žoga odskoči proti trdni površini in z vsakim odbojem izgubi višino. Vir: Self Made.

Rešitev

Tla so lahko objekt 1 v enačbi koeficienta restitucije. In vedno je v mirovanju, tako da:

$e=-\left (\frac-v_2-u_2 \right )=-\fracv_2u_2=-\fracvu$ Negativna smer je izbrana navzdol in pozitivna. Hitrost predmeta, ki se prosto sprošča z določene višine h_tudi je:

$u=-\sqrt2gh_o$ Znak (-) kaže, da se žoga spusti:

Lahko vam služi: Torricelli Experiment: Atmosferski tlačni ukrepi, pomen

$e= -\left (\fracv -\sqrt2gh_o \right )=0.82$

S to hitrostjo odskoči:

$v=+0.82 \sqrt2gh_o$

Znak + kaže, da gre za naraščajočo hitrost. In po njej žoga doseže največjo višino:

$h_1=\fracv^22g=\frac0.82^22gh_o2g=0.82^2h_o=0.6724.h_o$

Zdaj se spet vrne na tla s hitrostjo enake velikosti, vendar nasprotni znak:

$v=-0.82\sqrt2gh_o$ In odskoči z:

$v=0.82^2\sqrt2gh_o=0.6724\sqrt2gh_o$

To doseže največjo višino:

$h_1=\fracv^22g=\frac0.82^42gh_o2g=0.82^4h_o=0.4521.h_o$

Ponovno pridite do tal z:

$v=-0.82^2\sqrt2gh_o=-0.6724\sqrt2gh_o$

Zaporedni skoki

Vsakič, ko se žoga odbije in vzpenja, moraš hitrost spet pomnožiti za 0.82:

$v=0.82^3\sqrt2gh_o=0,5514\sqrt2gh_o$ In doseže največjo višino, ki jo določa kvadrat omenjene hitrosti:

$h_3=\frac0.82^62gh_o2g=0.304h_o$

V tej točki h₃ je približno 30% h_tudi. Kakšna bi bila višina ob 6. skokih, ne da bi morali izračunati tako podrobne kot prejšnji?

jaz bi bil h₆ = 0.82¹² h_tudi = 0.092H_tudi ali le 9% h_tudi.

-Vaja rešena 3

Blok 300 g se premika proti severu do 50 cm/s in se spopade proti 200 g bloku, ki je usmerjen na jug 100 cm/s. Predpostavimo, da je spopad popolnoma elastičen. Poiščite hitrosti po udarcu.

Podatki

m₁ = 300 g; ali₁ = + 50 cm/s

m₂ = 200 g; ali₂ = -100 cm/s

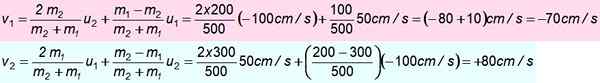
-Vaja rešena 4

Izpuščena je masa m₁ = 4 kg od točke, navedene na progi, brez trenja, dokler se ne trči v M₂ = 10 kg v mirovanju. Do kakšne višine je m₁ Po trku?

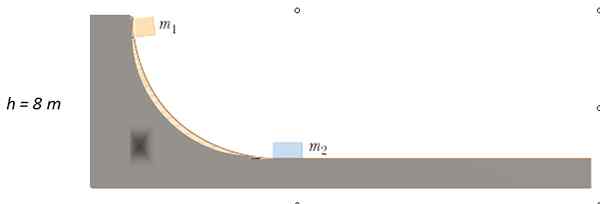
Rešitev

Ker ni trenja, se ohrani mehanska energija, da bi našli hitrost ali₁ s čim m₁ vplivi m_2.Sprva kinetična energija je 0, saj m₁ Del ostale. Ko se premikate po vodoravni površini, nima višine, zato je potencialna energija 0.

MGH = ½ mu₁ ²

$u_1=\sqrt2gh=\sqrt2\, .\, 9.8\, . \, 8\, m/s=12.5\, m/s$

ali₂ = 0

Zdaj hitrost m₁ Po trku:

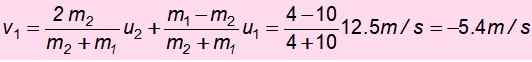
Negativni znak pomeni, da je bil vrnjen. S to hitrostjo se vzpenja in mehanska energija se spet ohrani H ', Višina, na kateri se uspe povzpeti po nesreči:

½ mV₁² = mgh '

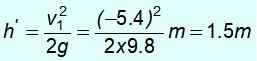
Upoštevajte, da se ne vrnete na izhodišče v višini 8 m. Nima dovolj energije, ker je del svoje kinetične energije dal maso m_1.

Reference

Giancoli, d. 2006. Fizika: načela z aplikacijami. 6^th. Ed Prentice Hall. 175-181
Rex, a. 2011. Osnove fizike. Pearson. 135-155.
Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Cengage učenje. 172 -182
Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo. 217-238
Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. MacGraw Hill. 185 -195

Elastični pretresi v dimenziji, posebnih primerih, vajah

Ohranjanje kinetične energije