Značilnosti pravokotnika

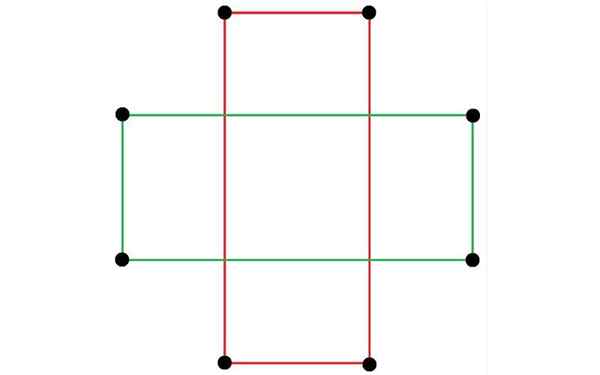
Dva pravokotnika. Vir: Tomruen, CC BY-SA 4.0, Wikimedia Commons

On pravokotnik Zanj je značilno, da je ravno geometrijska figura, ki ima štiri strani in štiri točke. Od teh štirih strani ima en par enak ukrep, drugi par pa drugačen ukrep.

Ta številka je paralelogramski poligon, saj so nasprotne strani pravokotnika vzporedne in imajo enake ukrepe. Koti, ki sestavljajo pravokotnike, imajo amplitudo 90 °, zato so ravni koti. Od tam prihaja ime pravokotnik.

Dejstvo, da imajo pravokotniki štiri kote iste amplitude, povzroči, da se te geometrijske figure imenujejo Equiángulos.

Ko pravokotnik prečka diagonalna črta, se ustvarita dva trikotnika. Če pravokotnik prečkamo z dvema diagonalnima črtama, bosta prečkala na sredini slike.

9 ključnih značilnosti pravokotnikov

1. Število strani in dimenzije

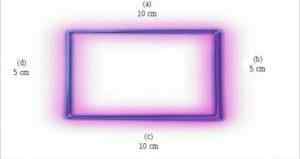
Pravokotniki so sestavljeni iz štirih strani. Te strani lahko razdelimo na dva para: en par strani meri enako, drugi navor pa ima višji ali nižji ukrepi kot prejšnji navor.

Strani, ki nasprotujejo, imajo enake ukrepe, medtem ko imajo zaporedne različne ukrepe.

Poleg tega so pravokotniki dve dimenzionalni številki, kar pomeni, da imajo le dve dimenziji: široke in visoke.

Vir: Wikipedia.org

2. Poligon

Pravokotniki so poligoni. V tem smislu so pravokotniki geometrijske figure, ki so omejene z zaprto poligonalno črto (to je segment ravne črte, ki se sam zapre).

Če smo natančnejši, so pravokotniki štirikotni poligoni, ker imajo štiri strani.

Lahko vam služi: isosceles trikotnik

3. Niso enakostranični poligoni

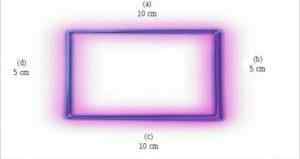
Poligon je enakostraničen, kadar vse njegove strani merijo enako. Strani pravokotnika nimajo enakih ukrepov. Zaradi tega ni mogoče reči, da so pravokotni enakostranični.

Vir: Wikipedia.org

4. Poligon z enaškim kotljem

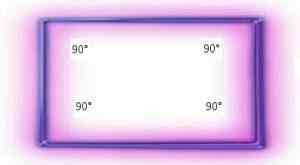
Poligoni Equiángulos so tisti, ki so sestavljeni iz kotov, ki imajo enako amplitudo.

Vsi pravokotniki so sestavljeni iz štirih ravnih kotov (to je 90 ° kotov). Pravokotnik 10 cm x 20 cm bo imel štiri 90 ° kote, enako se bo zgodilo z večjim ali manjšim pravokotnikom.

Vir: Wikipedia.org

5. Območje pravokotnika

Površina pravokotnika je enaka izdelku podstavka po višini, osnova je vodoravna stran, višina pa navpična stran. Preprostejši način, da ga vidite, da pomnoži ukrepe dveh sosednjih strani.

Formula za izračun območja te geometrijske številke je:

a = b x a

Nekaj ​​primerov izračuna območja pravokotnika je:

- Pravokotnik z osnovo 5 cm in 2 cm višine: 5 cm x 2 cm = 10 cm²

- Pravokotnik z osnovo 2 m in višino 0,5 m: 2 m x 0,5 m = 2 m²

- Pravokotnik z 18 m in višino 15 m: 18 m x 15 m = 270 m²

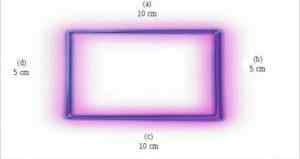Ta pravokotnik ima osnovo 10 cm in višino 5 cm. Vaše območje bo izdelek 10 cm x 5 cm. V tem primeru je površina pravokotnika 50 cm². Vir: Wikipedia.org

6. Pravokotniki so paralelogrami

Quadrilateral je mogoče razvrstiti v tri vrste: trapezoidi, trapezoidi in paralelograme. Za slednje je značilno, da imata dva para vzporednih strani, ki jim ni nujno, da bi imeli enake ukrepe.

V tem smislu so pravokotniki paralelogrami, saj se dva para strani obrneta.

Lahko vam služi: Prvo -stopinjska enačbe: formula, kako jih rešiti, primer, vaje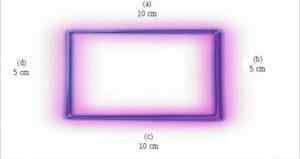Vir: Wikipedia.org

7. Nasprotni koti so skladni in zaporedni so komplementarni

Nasprotni koti so tisti, ki jih najdemo v nekomernih točkah slike. Medtem ko so zaporedni koti tisti, ki so sosednji, eden poleg drugega.

Dva kota sta skladna, kadar imata enako amplitudo. Po drugi strani pa se dva kota dopolnjujeta, ko vsota teh amplitud ustvari kot 180 °.

Vsi koti pravokotnika merijo 90 °, zato lahko rečemo, da so nasprotni koti te geometrijske figure skladni.

Glede na zaporedne kote je pravokotnik sestavljen iz 90 ° kotov. Če bodo dodane zaporedne, bo rezultat 180 °. Torej, to so dopolnilni koti.

8. Sestavljen je iz dveh pravokotnikov

Če je diagonala narisana v pravokotniku (črta, ki sega od kota pravokotnika do drugega nasprotnega), dobimo dva trikotnika pravokotnika. Ta vrsta trikotnika je tista, ki nastane z desnim kotom in dva akutna kota.

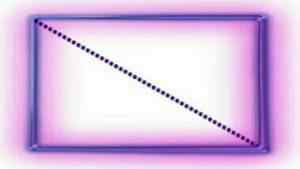Črta šiva predstavlja diagonalo. To deli pravokotnik na dva trikotnika. Vir: Wikipedia.org

9. Diagonale so razrezane na sredini

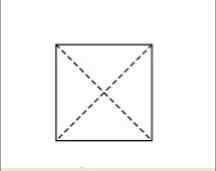
Kot je že pojasnjeno, so diagonale črte, ki segajo od enega od kotov do drugega nasprotnega kota. Če sta v pravokotniku narisana dva diagonala, bosta prečkala sredino slike.

Reference

1. Pravokotnik. Opomogel od MathisFuna.com.
2. Pravokotnik. Okreval od Merriam-Webster.com.
3. Lastnosti rombusov, pravokotnikov in kvadratov. Lutke so bile okrevane.com.
4. Pravokotnik. Pridobljeno iz.Wikipedija.org.
5. Pravokotnik. Okrevano od Collinsdiction in.com.

Vam lahko služi: multiplikativno inverzno: razlaga, primeri, rešene vaje