Vektorske zneske

Kaj so vektorski zneski?

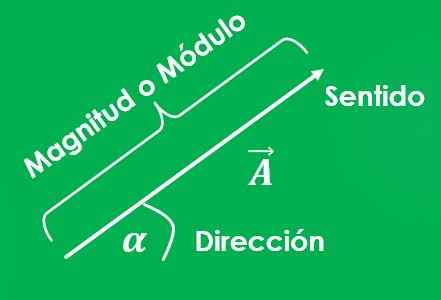
The Vektorska količina, ali vektor, kot je treba določiti tako velikost ali modul (z ustreznimi enotami) kot tudi njihov naslov.

Za razliko od vektorske količine ima skalarna količina le velikosti (in enote), vendar ne naslova. Nekaj ​​primerov skalarnih količin so temperatura, prostornina predmeta, dolžina, masa in čas, med drugim.

Razlika med vektorsko količino in plezanjem

V naslednjem primeru se lahko naučite razlikovati skalarno količino od vektorske količine:

Hitrost 10 km/h je skalarna količina, medtem ko je hitrost 10 km/h proti severu vektorska količina. Razlika je v tem, da je v drugem primeru poleg obsega določen naslov.

Vektorske količine imajo neskončnost aplikacij, zlasti v svetu fizike.

Grafika in označevanja vektorske količine

Način za označevanje vektorskega zneska je tako, da na črko postavite puščico (→), ki jo je treba uporabiti, ali s pisanjem pisma krepko (do).

Za grafiko vektorske količine je potreben referenčni sistem. V tem primeru bo kartezijanska ravnina uporabljena kot referenčni sistem.

Graf vektorja je črta, katere dolžina predstavlja velikost; in kot med omenjeno črto in osi x, merjeno v protirodnem smislu, predstavlja njegov naslov.

Določiti je treba, kakšno je izhodišče vektorja in kaj je točka prihoda. Na koncu črte je postavljena tudi puščica, ki kaže na točko prihoda, kar kaže na to, kakšna je smer vektorja.

Ko je referenčni sistem nastavljen, lahko vektor napišete kot urejen par: prva koordinata predstavlja njegovo velikost in drugo koordinacijo njegovega naslova.

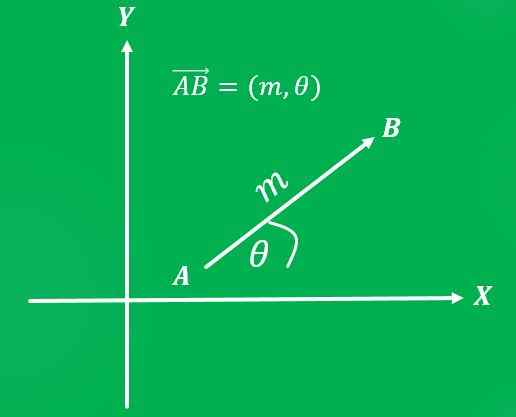
Primeri vektorskih zneskov

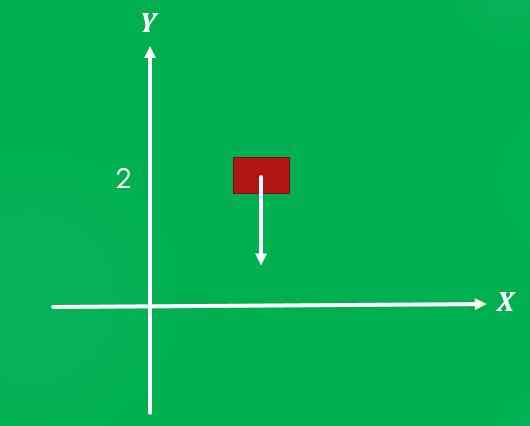
1- Gravitacija, ki deluje na predmet

Če je predmet postavljen na višino 2 metra nad tlemi in se sprosti, gravitacija nanj deluje z velikostjo 9,8 m/s² in smerjo, pravokotno na tla v smeri.

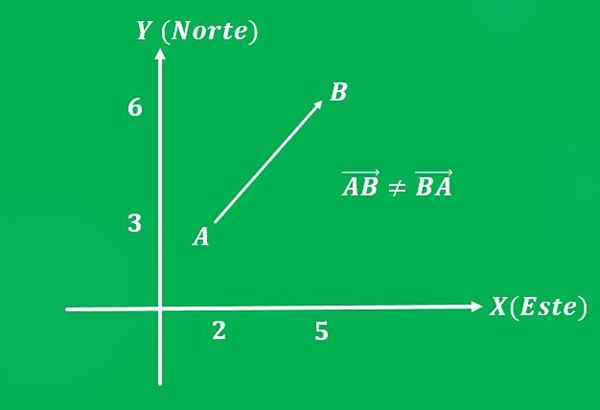
2- Gibanje letala

Letalo, ki se je premaknilo iz točke A = (2,3) do točke B = (5,6) kartezijanske ravnine, s hitrostjo 650 km/h (magnituda). Smer poti je 45 ° proti severovzhodu (kar pomeni).

Treba je opozoriti, da če je vrstni red obrnjen, ima vektor enako velikost in isto smer, vendar drugačen pomen, ki bo jugozahod.

3- sila, ki se uporablja za predmet

Juan se odloči, da bo potisnil stol s silo 10 kilogramov, v smeri vzporedne s tlemi. Možna čutila uporabne sile so: na levi ali desni (v primeru kartezijanske ravnine).

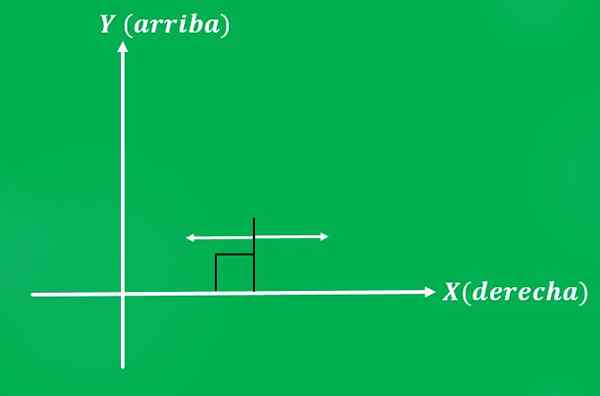
Kot tudi v prejšnjem primeru, pomen, da se Juan odloči, da bo dal silo, bo ustvaril drugačen rezultat.

To nam pove, da imata lahko dva vektorja enako velikost in smer, vendar sta drugačna (dajeta različne rezultate).

Lahko dodamo in odštejemo dva ali več vektorjev, za katere obstajajo zelo koristni rezultati, na primer zakon o paralelogramu. Vektor lahko pomnožite tudi s skalarnim.