Brezplačni koncept koncepta, enačbe, rešene vaje

The prosti pad Vertikalno gibanje, ki ga objekt doživi, ​​ko ga spusti z določene višine blizu površine zemlje. Je eden najpreprostejših in najbolj neposrednih gibov, ki so znani: v ravni črti in s stalnim pospeševanjem.

Vsi predmeti, ki so spuščeni ali se vržejo navpično navzgor ali navzdol, se premikajo s pospeševanjem 9.8 m/s² zagotavlja resnost Zemlje, ne glede na njegovo maso.

Prosti padec s pečine. Vir: Pexels.com.

To dejstvo je mogoče sprejeti danes brez težav. Vendar je bilo razumevanje resnične narave prostega padca nekaj časa. Grki so ga že opisali in zelo razlagali v bistvu proti četrtemu stoletju a c.

[TOC]

Enačbe gibanja prostega padca

Ko ste prepričani, da je pospešek enak za vsa telesa, ki se sprostijo pod delovanjem gravitacije, je čas, da vzpostavimo potrebne enačbe za razlago tega gibanja.

Pomembno je poudariti, da se v tem prvem gibalnem modelu ne upošteva zračne odpornosti. Vendar so rezultati tega modela zelo natančni in blizu resničnosti.

V vsem, kar sledi, bodo model delcev domnevali, da se dimenzije predmeta ne upoštevajo, ob predpostavki, da je celotna masa koncentrirana v eni točki.

Za enakomerno pospešeno pravokotno gibanje se jemlje kot osi, ki se sklicuje na osi in. Pozitiven smisel se sprejme in negativno navzdol.

Kinematične velikosti

Na ta način so enačbe položaja, hitrost in pospešek, odvisno od časa:

Pospešek

A = g = -9.8 m/s² (-32 čevljev/s²)

Položaj, odvisno od časa: in (t)

y = y_tudi + v_tudi . T + ½ gt²

Kje in_tudi To je začetni položaj mobilnega in v_tudi je začetna hitrost. Ne pozabite, da je v navpičnem zagonu začetna hitrost nujno drugačna od 0.

Ki je lahko zapisano kot:

in - in_tudi = v_tudi . T + ½ gt²

Δy = v_tudi . T + ½ gt²

Z δin je premik, ki ga je naredil mobilni delček. V enotah mednarodnega sistema sta položaj in premik podana v metrih (m).

Hitrost, odvisno od časa: V (t)

v = v_tudi + g . t

Hitrost, odvisno od premika

Možno je sklepati enačbo, ki povezuje premik s hitrostjo, ne da bi se vmešaval. Če želite to narediti, je čas zadnje enačbe očiščen:

Vam lahko služi: kvantni mehanski model atoma

 In nadomeščena je v enačbi premika:

Δy = v_tudi . T + ½ gt²

Trg je razvit s pomočjo izjemnega izdelka in izraze se preraste.

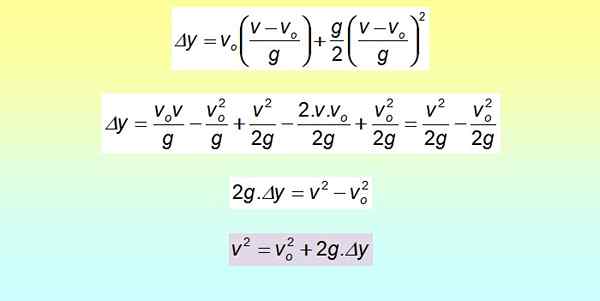
Ta enačba je uporabna, kadar čas ni na voljo, namesto tega pa obstajajo hitrosti in premiki, kot je razvidno iz oddelka rešenih primerov.

Primeri prostega padca

Pozorni bralec bo opazil prisotnost začetne hitrosti V_tudi. Prejšnje enačbe so veljavne za navpične gibe pod delovanjem gravitacije, tako ko predmet pade z določene višine, kot da ga vržejo navpično navzgor ali navzdol.

Ko predmet pade, se preprosto naredi v_tudi = 0 in enačbe so poenostavljene na naslednji način.

Pospešek

A = g = -9.8 m/s² (-32 čevljev/s²)

Položaj, odvisno od časa: in (t)

y = y_tudi+ ½ gt²

Hitrost, odvisno od časa: V (t)

v = g . t

Hitrost, odvisno od premika

v² = 2g. Dy

Dy Tudi negativno bo, saj v² To mora biti pozitiven znesek. To se bo zgodilo tako, če izvor tudi nič koordinatnega sistema na izstrelitveni točki ali na tleh.

Če ga bralec raje, lahko smeri smeri navzdol kot pozitivno. Gravitacija bo še naprej delovala, če se bo mislilo, da je + 9.8 m/s². Vendar morate biti skladni z izbrano konvencijo znakov.

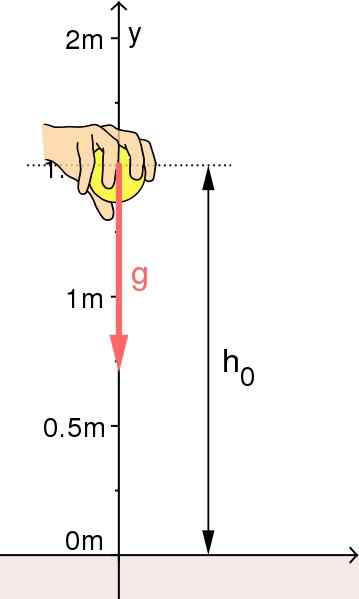Prosti padec predmeta: Izvor referenčnega sistema je bil izbran na terenu. Vir: Vir: Mikerun [CC BY-SA 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)]

Navpični zagon

Tukaj seveda začetna hitrost ne more biti nična. Predložiti moramo predmet, da se impulz dvigne. Glede na začetno hitrost se bo objekt dvignil na večjo ali manjšo višino.

Seveda se bo pojavil trenutek, ko se predmet na trenutke ustavi. Potem bo dosežena največja višina glede na izhodno točko. Tudi pospešek je še vedno G navzdol. Poglejmo, kaj se zgodi v tem primeru.

Izračun dosežene največje višine

Izbira me = 0:

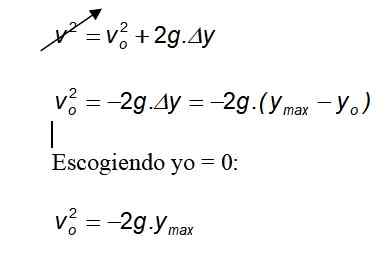
Ker gravitacija vedno kaže na tla v negativni smeri, se negativni znak prekliče.

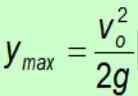
Največji izračun časa

Podoben postopek služi za iskanje časa, ki je potreben, da predmet doseže največjo višino.

v = v_tudi + g . t

To v = 0

v_tudi = - g . t_Max

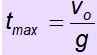
Čas leta je čas, ko predmet zdrži v zraku. Če se predmet vrne na izhodišče, je čas vzpona enak času spuščanja. Zato je čas letenja 2. T max.

Vam lahko služi: mikroskopska lestvica: lastnosti, štetje delcev, primeri

Je dvakrat t_Max Skupni čas, ki ga objekt zdrži v zraku? Da, dokler se objekt začne z točke in se vrne k njemu.

Če je izstrelitev narejena z določene višine na tleh in je objekt dovoljeno nadaljevati do tega, čas letenja ne bo več dvakrat večji od največjega časa.

Rešene vaje

Pri reševanju vaj, ki sledijo, bo upoštevano naslednje:

1-višina, kjer je predmet spuščeno, je majhna v primerjavi s polmerom zemlje.

2-Zračna odpornost je zaničljiva.

3-Vrednost pospeška gravitacije je 9.8 m/s²

4-Ko gre za težave z enim samim mobilnikom, je po možnosti izbran in_tudi = 0 na izhodišču. To običajno olajša izračune.

5-AT manj kot nasprotno, je smer navzgor jemlje kot pozitivna.

6 -Vzpon in padajoči kombinirani gibi, uporabljene enačbe neposredno ponujajo pravilne rezultate, dokler se doslednost vzdržuje z znaki: Pozitivno navzgor, navzdol, negativno in resnost -9.8 m/s² ali -10 m/s² Če se raje zaokrožite (za več udobja pri izračunu).

Vaja 1

Žoga se vrže navpično s hitrostjo 25.0 m/s. Odgovorite na naslednja vprašanja:

a) koliko se dvigne?

b) Kako dolgo traja, da dosežete svojo najvišjo točko?

c) Kako dolgo traja kroglica, da se dotakne površine zemlje, potem ko doseže svojo najvišjo točko?

d) kakšna je vaša hitrost, ko se vrnete na raven, kje se je začela?

Rešitev

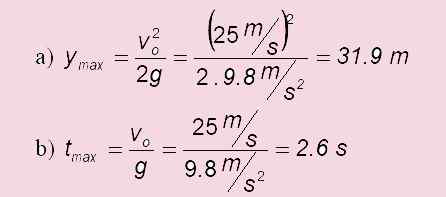
c) V primeru lansiranja ravni: t_let = 2 . t_Max = 2 x6 s = 5.1 s

d) Ko se vrne v izhodišče, ima hitrost enako velikost kot začetna hitrost, vendar nasprotna smer, zato mora biti - 25 m/s. Zlahka ga preverimo z zamenjavo vrednosti v enačbi za hitrost:

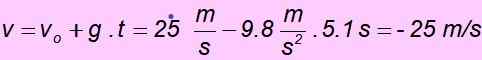
Vaja 2

Majhen poštni kovček se sprosti iz helikopterja, ki se spušča s konstantno hitrostjo 1.50 m/s. Po 2.00 S Izračunajte:

a) kakšna je hitrost kovčka?

b) Kako daleč je kovček pod helikopterjem?

c) Kateri so vaši odgovori za razdelke a) in b) Če se helikopter dvigne s konstantno hitrostjo 1.50 m/s?

Rešitev

Oddelek a

Ko kovček opusti helikopter, ima zato začetno hitrost tega v_tudi = -1.50 m/s. Z navedenim časom se je hitrost povečala zahvaljujoč pospeševanju gravitacije:

Vam lahko služi: nebesna telesa

v = v_tudi + g . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Oddelek b

Poglejmo, koliko se je kovček spustil glede na izhodišče v tistem času:

Kovček: Dy = v_tudi . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Izbrano je in_tudi = 0 Na izhodišču, kot je navedeno na začetku odseka. Negativni znak kaže, da se je kovček spustil 22. 6 m pod izhodišče.

Medtem helikopter Padlo je hitro -1.50 m/s, nenehno predpostavljamo, zato je v določenem času 2 sekund helikopter potoval:

Helikopter: δy = v_tudi.t = -1.petdeset x 2 m = -3 m.

Zato se po dveh sekundah kovček in helikopter ločita na razdaljo od:

D =| -22.6 - (-3) | M = 19. 6 m.

Razdalja je vedno pozitivna. Za poudarjanje tega dejstva se uporablja absolutna vrednost.

Oddelek c

Ko se helikopter dvigne, ima hitrost + 1.5 m/s. S to hitrostjo izide kovček, tako da po 2 S že nosi:

v = v_tudi + g . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Hitrost se izkaže za negativno, saj se po dveh sekundah kovček premika navzdol. Se je povečal zahvaljujoč gravitaciji, vendar ne toliko kot v oddelku A.

Zdaj bomo ugotovili, koliko se je kovček spustil glede na izhodišče v prvih dveh sekundah potovanja:

Valija: δy = v_tudi . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Medtem helikopter Je dvignil Glede izhodišča in je to storil s konstantno hitrostjo:

Helikopter: δy = v_tudi.T = +1.petdeset x 2 m = +3 m.

Po 2 sekundah kovček in helikopter ločimo z razdaljo od:

D =| -16.6 - (+3) | M = 19.6 m

Razdalja, ki jih loči, je v obeh primerih enaka. Kovček v drugem primeru prevozi manj navpično razdaljo, ker je bila njegova začetna hitrost usmerjena navzgor.

https: // youtu.biti/w2uvetxwsfk

Reference

1. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje.  23 - 27.
2. Rex, a. 2011. Osnove fizike. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14^th. Ed. Zvezek1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Osnove fizike. 9^na Ed. Cengage učenje. 43 - 55.
5. Wilson, J. 2011. Fizika 10. Pearson Education. 133 - 149.