Trenutna opredelitev hitrosti, formula, izračun in vaje

The trenutna hitrost Opredeljen je kot trenutna sprememba premika skozi čas. To je koncept, ki dodaja veliko natančnost preučevanju gibanja. In to je napredek glede na povprečno hitrost, katere informacije so zelo splošne.

Za pridobitev trenutne hitrosti si oglejmo čim manjši časovni interval. Diferencialni računalnik je odlično orodje za matematično izražanje te ideje.

Trenutna hitrost predstavlja mobilno hitrost na vsaki točki svoje poti. Vir: Pixabay.

Izhodišče je povprečna hitrost:

Zdaj pa Δt pristopimo k 0 vsem, kar lahko. To je meja in rezultat bo natančno trenutna hitrost:

Ta meja je znana po imenu izpeljane. V zapisu o diferencialnem izračunu imate:

Pod pogojem, da je gibanje omejeno na ravno črto, ga je mogoče izpustiti z vektorskim zapisom.

[TOC]

Izračun takojšnje hitrosti: geometrijska razlaga

Naslednja slika prikazuje geometrijsko razlago koncepta derivata: to je nagib črte tangenta Do krivulje x (t) vs. t Na vsaki točki.

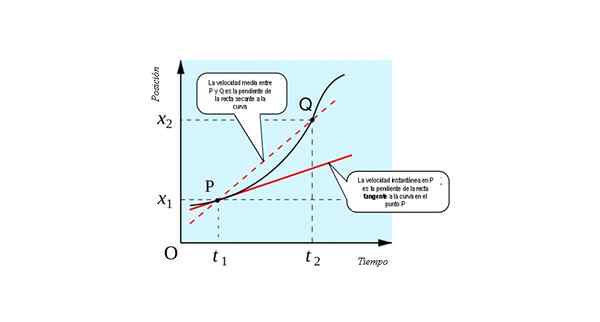Trenutna hitrost v P ekvivalentu številčno do naklona črte tangenta do krivulje x Vs. T v točki P. Vir: Vir: すじにく シチュー [CC0].

Lahko si predstavljate, kako pridobiti mejo, če se točka Q postopoma bliža. Prišel bo čas, ko bosta obe točki tako blizu, da je ni mogoče razlikovati od drugega.

Linija, ki jih združuje, se bo nato sušila (naravnost, ki se razreže na dve točki), da bo tangentna (naravnost, ki se dotakne krivulje v eni točki). Zato bi morali najti takojšnjo hitrost mobilnega delca:

• Graf položaja delca kot funkcija časa. Če najdete naklon črte tangenta do krivulje, imate takojšnjo hitrost pri vsaki točki, ki jo zaseda delček.

Lahko vam služi: Ampère zakon: formula in enačbe, demonstracije, vaje

O No:

• Funkcija položaja delcev x (t), ki izhaja za pridobitev funkcije hitrosti V (t), potem se vsakič oceni ta funkcija t, Udobje. Funkcija položaja naj bi bila izpeljana.

Nekaj ​​posebnih primerov pri izračunu trenutne hitrosti

-Nagib črte, tangenta na krivuljo v P, je 0. NULL naklon pomeni, da je mobilni telefon ustavljen in da je njegova hitrost seveda 0.

-Nagib črte tangenta na krivuljo v P je večji od 0. Hitrost je pozitivna. V zgornjem grafu pomeni, da se mobilni telefon oddalji od oz.

-Nagib črte, tangenta na krivuljo v P, je manjši od 0. Hitrost bi bila negativna. V zgornjem grafu ni takšnih točk, toda v tem primeru bi se delček približal oz.

-Nagib črte tangenta do krivulje je stalen v P in vseh drugih točkah. V tem primeru je graf ravno črta in mobilni telefon ima Enotno gibanje linij MRU (njegova hitrost je konstantna).

Na splošno funkcija V (t) To je tudi časovna funkcija, ki je posledično izpeljana. Kaj pa, če ne bi bilo mogoče najti tiste, ki izhajajo iz funkcij x (t) in V (t)?

V primeru x (t) Mogoče je, da je naklon - trenutna hitrost - močno spremenil znake. Ali pa bo takoj prešlo od nič do druge vrednosti.

Če je tako, grafika x (t) Predstavil bi nasvete ali vogale ob nenadnih spremembah. Zelo drugačen od primera, predstavljenega na prejšnji sliki, v kateri je krivulja x (t) To je mehka krivulja, brez točk, vogalov, diskontinuitet ali nenadnih sprememb.

Vam lahko služi: Bose Einstein kondenzat

Resnica je, da so za prave mobilne telefone mehke krivulje tiste, ki najbolje predstavljajo vedenje predmeta.

Splošno gibanje je precej zapleteno. Mobile lahko nekaj časa ustavite, pospešite, da se premaknete od počitka, da se hitrost in se oddalji od izhodišča, nekaj časa zadržite hitrost, nato pa se ustavite, da se spet ustavite in s tem slog.

Lahko začnejo znova in nadaljujejo v isti smeri. Ali ukrepajte in se vrnite. Temu pravimo raznoliko gibanje v dimenziji.

Spodaj bo nekaj primerov izračuna trenutne hitrosti razjasnilo uporabo danih definicij:

Rešene trenutne vaje za hitrost

Vaja 1

Delci se premika po ravni črti z naslednjim zakonom o gibanju:

x (t) = -t³ + 2 t² + 6 T - 10

Vse enote so v mednarodnem sistemu. Najti:

a) položaj delca pri t = 3 sekunde.

b) Povprečna hitrost v intervalu med t = 0 s in t = 3 s.

c) Povprečna hitrost v intervalu med t = 0 s in t = 3 s.

d) trenutna hitrost delca prejšnjega vprašanja, pri t = 1 s.

Odgovori

a) Če želite najti položaj delca, zakon o gibanju (položaj položaja) pri t = 3:

x (3) = (-4/3).3³ + 2. 3² ₊ 6.3 - 10 m = -10 m

Ni problema, da je položaj negativen. Znak (-) kaže, da je delček levo od izvora oz.

b) Pri izračunu povprečne hitrosti so v določenih časih potrebni končni in začetni položaji delca: x (3) in x (0). Položaj pri t = 3 je x (3) in je znan o prejšnjem rezultatu. Položaj pri t = 0 sekundah je x (0) = -10 m.

Vam lahko služi: statična: zgodovina, kakšne študije, aplikacije, zakoni

Ker je končni položaj enak začetnemu, se takoj sklepa, da je povprečna hitrost 0.

c) Povprečna hitrost je razlog med prevoženo razdaljo in porabljenim časom. Zdaj je razdalja modul ali velikost premika:

Razdalja = | x2 - x1 | = | -10-(-10) | M = 20 m

Upoštevajte, da je prevožena razdalja vedno pozitivna.

v_{M = 20 m/3 s = 6.7 m/s}

d) Tu je treba najti prvi izpeljan položaja glede časa. Potem se oceni za t = 1 sekundo.

x '(t) = -4 t² + 4 T + 6

x '(1) = -4.1² + 4.1 + 6 m/s = 6 m/s

Vaja 2

Spodaj je graf položaja mobilnega telefona kot funkcije časa. Poiščite takojšnjo hitrost pri t = 2 sekundi.

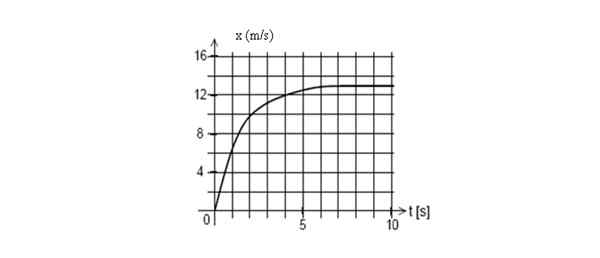Graf položaja v primerjavi s časom za mobilni telefon. Vir: Self Made.

Odgovor

Tangentno črto narišite na krivuljo pri t = 2 sekundi, nato izračunajte pobočje, pri čemer vzamete dve točki črte.

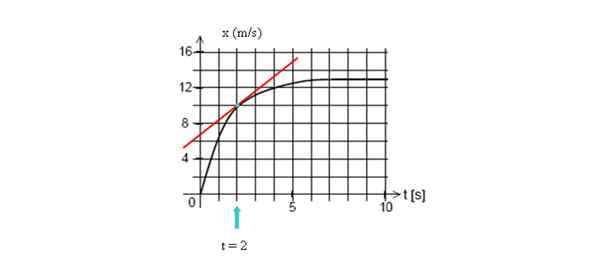Če želite izračunati takojšnjo hitrost na navedeni točki, narišite tangentno črto do te točke in poiščite njegov naklon. Vir: Self Made.

V tem primeru bomo vzeli dve točki, ki sta zlahka vizualizirani, katerih koordinate so (2 s, 10 m) in rez z navpično osi (0 s, 7 m):

Reference

1. Giancoli, d. Fizika. Načela z aplikacijami. 6^th Izdaja. Dvorana Prentice. 22-25.
2. Resnick, r. (1999). Fizično. Zvezek 1. Tretja izdaja v španščini. Mehika. Continental uredništvo s.Do. od c.V. 21-22.
3. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7^ma. Izdaja. Mehika. Uredniki učenja Cengage. 23-25.